© Барна Р., 2021
Серія "Вчимось разом" до підручника
"Математика 4 клас Скворцова С., Онопрієнко О."
Сторінка 28
Завдання 1
1) Множення можна замінити додаванням однакових доданків:
68 • 4 = 68 + 68 + 68 + 68 = 272
2) Розподільний закон множення відносно додавання:
68 • 4 = (60 + 8) • 4 = 60 • 4 + 8 • 4 = 240 + 32 = 272
3) Сполучний закон множення:
68 • 4 = 68 • (2 • 2) = (68 • 2) • 2 = 136 • 2 = 272
Завдання 2
23 • 1 : 23 + 0 = 23 : 23 + 0 = 1 + 0 = 1
160 : 1 • 3 : 480 = 160 • 3 : 480 = 480 : 480 = 1
0 • (120 – 3 • З0) : 67 = 0 • (120 – 90) = 0
0 : (5 • 42 : 70) = 0
Завдання 3
(240 + 480) : 80 = 240 : 80 + 480 : 80 = 3 + 6 = 9
5 • (2 • 67) = (5 • 2) • 67 = 10 • 67 = 670
(720 – 540) : 9 = 720 : 9 – 540 : 9 = 80 – 60 = 20
Завдання 4 Складена задача на знаходження суми частин
Діти зібрали природні матеріали: жолудів — 240, шишки становили 1/8 від кількості жолудів, а каштани — 1/3 від кількості жолудів. Скільки всього шишок і каштанів зібрали діти?
Короткий запис
Шишки — ?, 1/8 від 240 штук
Каштани — ?, 1/3 від 240 штук
Всього — ?
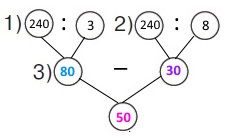
Схема
Вираз 240 : 3 + 240 : 8
Розв’язання
1) 240 : 8 = 30 (ш.) – шишок зібрали діти.
2) 240 : 3 = 80 (к.) – каштанів зібрали діти.
3) 30 + 80 = 110 (шт.) – всього шишок і каштанів зібрали діти.
Відповідь: діти зібрали 110 шишок і каштанів.
Змінили запитання задачі так, щоб у її розв'язанні останньою була дія віднімання, отримали складену задачу на різницеве порівняння.
|
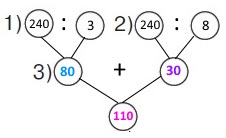
Діти зібрали природні матеріали: жолудів — 240, шишки становили 1/8 від кількості жолудів, а каштани — 1/3 від кількості жолудів. На скільки більше зібрали каштанів, ніж шишок? Короткий запис Шишки — ?, 1/8 від 240 штук Каштани — ?, 1/3 від 240 штук; на ? штук більше Схема
Вираз (240 : 3) – (240 : 8) |
Діти зібрали природні матеріали: жолудів — 240, шишки становили 1/8 від кількості жолудів, а каштани — 1/3 від кількості жолудів. На скільки менше зібрали шишок, ніж каштанів? |
Змінили запитання задачі так, щоб у її розв'язанні останньою була дія ділення, отримали складену задачу на кратне порівняння.
|
Діти зібрали природні матеріали: жолудів — 240, шишки становили 1/8 від кількості жолудів, а каштани — 1/3 від кількості жолудів. У скільки разів більше зібрали жолудів, ніж каштанів? Короткий запис Жолуді — 240 штук; у ? разів більше, ніж каштанів Каштани — ?, 1/3 від 240 штук; Схема
Вираз 240 : (240 : 3) |
Діти зібрали природні матеріали: жолудів — 240, шишки становили 1/8 від кількості жолудів, а каштани — 1/3 від кількості жолудів. У скільки разів менше зібрали каштанів, ніж жолудів? |
Завдання 5 Рівняння
|
6 • p = 96 + 84 6 • р = 180 р = 180 : 6 р = 30 6 • 30 = 180 96 + 84 = 180 180 = 180 |
80 • 7 – с = 390 560 – с = 390 с = 560 – 390 с = 170 80 • 7 – 170 = 560 – 170 = 390 390 = 390
|
k • 50 + 160 = 760 k • 50 = 760 – 160 k • 50 = 600 k = 600 : 50 k = 12 12 • 50 + 160 = 760 760 = 760 |
Сторінка 29
Завдання 1
Порозрядне додавання з переходом через розряд:
380 + 240 = (300 + 80) + (200 + 40) = 500 + 120 = 620
Порозрядне віднімання з переходом через розряд:
730 – 450 = (600 + 120) – (400 + 50) = (600 – 400) + (120 – 50) = 200 + 80 = 280
Розподільний закон ділення відносно додавання:
234 : 3 = (210 + 24) : 3 = 210 : 3 + 24 : 3 = 70 + 8 = 78
Розподільний закон множення відносно додавання:
234 • 3 = (200 + 30 + 4) • 3 = 200 • 3 + 30 • 3 + 4 • 3 = 600 + 90 + 12 = 702
Завдання 2
|
+478 327 805 |
+478 327 109 914 |
_809 478 331 |
_1000 308 692 |
Завдання 3 Множення доводимо додаванням
256 • 3 = 256 + 256 + 256 = 600 + 150 + 18 = 768
356 • 2 = 356 + 356 = 600 + 100 + 12 = 712
189 • 4 = 189 + 189 + 189 + 189 = (200 + 160 + 18) + 189 + 189 = 378 + 378 = 600 + 140 + 16 = 756
Завдання 4
|
Письмове додавання +264 264 264 792 |
Множення замінили сумою однакових доданків: 264 • 3 = 264 + 264 + 264 = = 600 + 180 + 12 = 792 |
|
х264 3 792 |
Розподільний закон множення відносно додавання: 264 • 3 = (200 + 60 + 4) • 3 = = 200 • 3 + 60 • 3 + 4 • 3 = = 600 + 180 + 12 = 792 |
Сторінка 30
Завдання 5, 6
|
х156 4 624 |
х285 3 855 |
х165 4 660 |
х398 2 796 |
х326 3 978 |
|
6 • 4 = 24 5 • 4 = 20 1 • 4 = 4 |
5 • 3 = 15 8 • 3 = 24 2 • 3 = 6 |
5 • 4 = 20 6 • 4 = 24 1 • 4 = 4 |
8 • 2 = 16 9 • 2 = 18 3 • 2 = 6 |
6 • 3 = 18 2 • 3 = 6 3 • 3 = 9 |
Завдання 7
1) Задача на зведення до одиниці
За 7 однакових баночок кінетичного піску заплатили 420 грн. Скільки треба заплатити за 3 такі баночки?
Короткий запис
7 баночок — 420 грн
3 баночки — ? грн
Схема
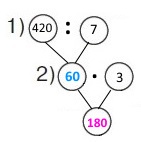
Вираз 420 : 7 • 3
Розв’язання
1) 420 : 7 = 60 (грн) – треба заплатити за 1 баночку.
2) 60 • 3 = 180 (грн) – треба заплатити за 3 баночки.
Відповідь: треба заплатити 180 гривень.
2) Задача на знаходження пропорційного
За 7 однакових баночок кінетичного піску заплатили 420 грн. Скільки треба заплатити за 3 такі баночки під час розпродажу, якщо ціна баночки знизилася на 18 грн?
|
Ціна (грн) |
Кількість (б.) |
Вартість (грн) |
|
? |
7 |
420 |
|
?, на 18 грн менше |
3 |
? |
Короткий запис
7 баночок — 420 грн; 1 баночка — ? грн
3 баночки — ? грн; 1 баночка — ?, на 18 грн менше
Схема
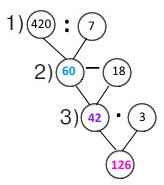
Вираз (420 : 7 – 18) • 3
Розв’язання
1) 420 : 7 = 60 (грн) – треба заплатити за 1 баночку.
2) 60 – 18 = 42 (грн) – ціна баночки під час розпродажу.
3) 42 • 3 = (40 + 2) • 3 = 126 (грн) – треба заплатити за 3 баночки під час розпродажу.
Відповідь: під час розпродажу треба заплатити 126 гривень.
Сторінка 31
Завдання 1 Розподільний закон множення відносно додавання
338 • 2 = (300 + 30 + 8) • 2 = 300 • 2 + 30 • 2 + 8 • 2 = 600 + 60 + 16 = 676
Завдання 2 Переставний закон множення (а • b = b • а)
|
3 • 328 = 328 • 3 = 984 5 • 179 = 179 • 5 = 895 4 • 246 = 246 • 4 = 984 2 • 437 = 437 • 2 = 874 |
х328 3 984 |
х179 5 895 |
х246 4 984 |
х437 2 874 |
Завдання 3
Якщо один із множників дорівнює 0, тоді добуток дорівнює 0 (а • 0 = 0 • а = 0):
72 • 2 • (188 – 99) • 0 • (328 – 176) = 0
При діленні однакових чисел отримаємо 1 (а : а = 1):
(654 + 247 – 409) : (247 + 654 – 409) = 1
Число не зміниться, якщо його помножити на 1 (а • 1 = 1 • а = а):
(473 + 238 – 373) • 1 = 473 + 238 – 373 = 338
Якщо нуль поділити на будь-яке ненульове число, тоді отримаємо 0 (0 : а = 0, при а ≠0):
0 : (567 + 398 – 288 +180 : 6) = 0
Число не зміниться, якщо його поділити на 1 (а : 1 = а):
(470 + 280 – 270) : 1 = 470 + 280 – 270 = 480
Потрібне обчислення:
(367 + 533) : 10 = (800 + 90 + 10) : 10 = 900 : 10 = 90
Завдання 4 Множення способом укрупнення розрядів
0 д. • 7 = 0 д. = 0 1 с. • 9 = 9 с. = 900 0 од. • 5 = 0 од. = 0 1 д. • 8 = 8 д. = 80
Завдання 5
|
х324 3 972 |
х407 2 814 |
х239 4 956 |
х324 3 972 |
х127 6 762 |
х306 3 918 |
х189 5 945 |
х408 2 816 |
|
4 • 3 = 12 2 • 3 = 6 3 • 3 = 9 |
7 • 2 = 14 4 • 2 = 8 |
9 • 4 = 36 3 • 4 = 12 2 • 4 = 8 |
4 • 3 = 12 2 • 3 = 6 3 • 3 = 9 |
7 • 6 = 42 2 • 6 = 12 1 • 6 = 6 |
6 • 3 = 18 3 • 3 = 9 |
9 • 5 = 45 8 • 5 = 40 1 • 5 = 5 |
8 • 2 = 16 4 • 2 = 8 |
Сторінка 32
Завдання 6
1) Складена задача на ділення на вміщення суми
Для наповнення дитячого басейну місткістю 352 л використовують кран і помпу. Щохвилини через кран наливається 9 л води, а помпа накачує 23 л. За який час наповниться басейн, якщо працюватимуть і кран, і помпа?
|
|
Літрів за 1 хв |
Кількість хвилин |
Загальна кількість літрів |
|
Кран |
9 |
|
|
|
Помпа |
23 |
|
|
|
Всього |
? |
? |
352 |
Короткий запис
352 літри — це ? хвилин по ? (9 л і 23 л)
Схема
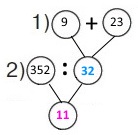
Вираз 352 : (9 + 23)
Розв’язання
1) 9 + 23 = 23 + 7 + 2 = 32 (л) – всього літрів води наливається щохвилини.
2) 352 : 32 = (320 + 32) : 32 = 11 (хв) – час наповнення басейну.
Відповідь: басейн наповниться за 11 хвилин.
2) Складена задача на ділення на вміщення різниці
Щохвилини в басейн місткістю 352 л через кран наливається 9 л води, а через зливний отвір виливається 1 л води. За який час басейн наповниться?
Короткий запис
352 літри — це ? хвилин по ? (9 л без 1 л)
Схема
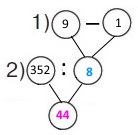
Вираз 352 : (9 – 1)
Розв’язання
1) 9 – 1 = 8 (л) – літрів води наливається щохвилини.
2) 352 : 8 = (320 + 32) : 8 = 44 (хв) – час наповнення басейну.
Відповідь: басейн наповниться за 44 хвилини.
Завдання 7
|
Ділення з остачею |
Перевірка |
|
42 : 4 = 10 (ост. 2) 37 : 10 = 3 (ост. 7) 49 : 8 = 6 (ост. 1) 27 : 5 = 5 (ост. 2) 84 : 9 = 9 (ост. 3) 40 : 6 = 6 (ост. 4) 69 : 10 = 6 (ост. 9) 80 : 9 = 8 (ост. 8) 70 : 12 = 5 (ост. 10) 30 : 4 = 7 (ост. 2) |
10 • 4 + 2 = 40 + 2 = 42 3 • 10 + 7 = 30 + 7 = 37 6 • 8 + 1 = 48 + 1 = 49 5 • 5 + 2 = 25 + 2 = 27 9 • 9 + 3 = 81 + 3 = 84 6 • 6 + 4 = 36 + 4 = 40 6 • 10 + 9 = 60 + 9 = 69 8 • 9 + 8 = 72 + 8 = 80 5 • 12 + 10 = 60 + 10 = 70 7 • 4 + 2 = 28 + 2 = 30 |
Завдання 8
|
430 + р = 180 • 5 430 + р = 900 р = 900 – 430 р = 470 430 + 470 = 900 180 • 5 = 900 900 = 900 |
3 • 140 : k = 7 420 : k = 7 k = 420 : 7 k = 60 3 • 140 : 60 = 7 7 = 7 |
420 – x = 180 • 2 420 – x = 360 x = 420 – 360 x = 60 420 – 60 = 360 180 • 2 = 360 360 = 360 |
Сума коренів рівнянь: 470 + 60 + 80 = 470 + 140 = 500 + 110 = 610
Завдання 9 Порядок дій
|
720 : (450 : 50) + 400 : 8 = 130 1) 450 : 50 = 45 : 5 = 9 2) 720 : 9 = 80 3) 400 : 8 = 50 4) 80 + 50 = 80 + 20 + 30 = 130 |
(518 – 487) • (720 : 80) – 86 = 193 1) 518 – 487 = 518 – 500 + 13 = 18 + 13 = 31 2) 720 : 80 = 72 : 8 = 9 3) 31 • 9 = (30 + 1) • 9 = 270 + 9 = 279 4) 279 – 86 = 179 + (100 – 86) = 179 + 14 = 193 |
|
600 : (480 : 80) • 9 : 30 = 30 1) 480 : 80 = 48 : 8 = 6 2) 600 : 6 = 100 3) 100 • 9 = 900 4) 900 : 30 = 90 : 3 = 30 |
572 + 248 – 320 : 160 • 50 = 720 1) 320 : 160 = 32 : 16 = 2 2) 2 • 50 = 100 3) 572 + 248 = 700 + 110 + 10 = 820 4) 820 – 100 = 720 |
Завдання 10 Троє хлопчиків зібрали 36 мушель. Коли перший хлопчик виділив для піщаного замку 2 мушлі, другий — 4, а третій — 6, у кожного залишилося мушель порівну. Скільки мушель зібрав кожний хлопчик?
Розв’язання
1) 2 + 4 + 6 = 12 (м.) – всього мушель виділили для замку.
2) 36 – 12 = 24 (м.) – мушель залишилося у хлопчиків, причому порівну в кожного.
3) 24 : 3 = 8 (м.) – мушель залишилося в кожного хлопчика.
4) 8 + 2 = 10 (м.) – мушель зібрав І хлопчик.
5) 8 + 4 = 12 (м.) – мушель зібрав ІІ хлопчик.
6) 8 + 6 = 14 (м.) – мушель зібрав ІІІ хлопчик.
Відповідь: І хлопчик зібрав 10 мушель, ІІ – 12 мушель, ІІІ – 14 мушель.
Сторінка 33
Завдання 1
(78 : 13 + 102 : 17) • 8 : 32 • 27 – 19 = 62
1) 78 : 13 = 6
2) 102 : 17 = 6
3) 6 + 6 = 12
4) 12 • 8 = (10 + 2) • 8 = 80 + 16 = 96
5) 96 : 32 = 96 : (8 • 4) = 96 : 8 : 4 = 12 : 4 = 3
6) 3 • 27 = 3 • (20 + 7) = 60 + 21 = 81
7) 81 – 19 = 81 – 20 + 1 = 62
Завдання 2
1) Задача на зведення до одиниці (можна розв’язати двома способами)
Із 12 м тканини кравчиня пошила 3 однакові скатертини. Скільки метрів тканини потрібно, щоб пошити 6 таких скатертин?
Короткий запис
3 скатертини — 12 м
6 скатертин — ? м
Розв’язання
1) 12 : 3 = 4 (м) – метрів тканини потрібно на скатертину.
2) 4 • 6 = 24 (м) – метрів тканини потрібно на шість скатертин.
2 спосіб (відношень)
1) 6 : 3 = 2 (рази) – у стільки разів більше треба пошити скатертин.
2) 12 • 2 = 24 (м) – метрів тканини потрібно на шість скатертин.
Відповідь: потрібно 24 метри тканини.
2) Задача на зведення до одиниці (можна розв’язати тільки способом відношень)
Із 10 м тканини кравчиня пошила 3 скатертини. Скільки метрів тканини потрібно, щоб пошити 6 таких скатертин?
Короткий запис
3 скатертини — 10 м
6 скатертин — ? м
Розв’язання
1) 6 : 3 = 2 (рази) – у стільки разів більше треба пошити скатертин.
2) 10 • 2 = 20 (м) – метрів тканини потрібно на шість скатертин.
Відповідь: потрібно 24 метри тканини.
Сторінка 34
Завдання 3 Задачу на зведення до одиниці можна розв’язати тільки способом відношень
За 3 с в басейн Фонтану чотирьох річок наливається 10 л води. Скільки літрів води наллється в басейн фонтану за 6 с?
Короткий запис
3 с — 10 л
6 с — ? л
Розв’язання
1) 6 : 3 = 2 (рази) – у стільки разів більше потрібно часу.
2) 10 • 2 = 20 (л) – літрів води наллється в басейн.
Відповідь: у басейн наллється 20 літрів води.
Завдання 4 Задачу на зведення до одиниці можна розв’язати тільки способом відношень
За 5 с в басейн Фонтану чотирьох річок наливається 12 л води. Скільки літрів води наллється в басейн фонтану за 10 с?
Короткий запис
5 с — 12 л
10 с — ? л
Розв’язання
1) 10 : 5 = 2 (рази) – у стільки разів більше потрібно часу.
2) 12 • 2 = 12 + 12 = 24 (л) – літрів води наллється в басейн.
Відповідь: у басейн наллється 24 літрів води.
Завдання 5
1) Задачу на зведення до одиниці можна розв’язати тільки способом відношень
У клініці для диких тварин чотирьом леопардам дають на день 14 кг м'яса. Скільки кілограмів м'яса дають на день двом леопардам за однакової норми годування?
Короткий запис
4 леопарди — 14 кг
2 леопарди — ? кг
Розв’язання
1) 4 : 2 = 2 (рази) – у стільки разів менше леопардів.
2) 14 : 2 = 7 (кг) – м’яса дають двом леопардам.
Відповідь: двом леопардам дають 7 кілограмів м’яса.
2) Змінили умову так, щоб задачу на зведення до одиниці можна розв’язати двома способами
У клініці для диких тварин чотирьом леопардам дають на день 12 кг м'яса. Скільки кілограмів м'яса дають на день двом леопардам за однакової норми годування?
Короткий запис
4 леопарди — 12 кг
2 леопарди — ? кг
Розв’язання
1) 12 : 4 = 3 (кг) – м’яса дають 1 леопардові.
2) 3 • 2 = 6 (кг) – м’яса дають двом леопардам.
2 спосіб (відношень)
1) 4 : 2 = 2 (рази) – у стільки разів менше леопардів.
2) 12 : 2 = 6 (кг) – м’яса дають двом леопардам.
Відповідь: двом леопардам дають 7 кілограмів м’яса.
Завдання 6
|
х368 2 736 |
х328 3 984 |
х102 4 408 |
х232 4 928 |
Завдання 7
|
Ділення з остачею |
Перевірка |
|
67 : 8 = 8 (ост. 3) 14 : 6 = 2 (ост. 2) 36 : 10 = 3 (ост. 6) 30 : 8 = 3 (ост. 6) 32 : 10 = 3 (ост. 2) 12 : 5 = 2 (ост. 2) |
8 • 8 + 3 = 64 + 3 = 7 2 • 6 + 2 = 12 + 2 = 14 3 • 10 + 6 = 30 + 6 = 36 3 • 8 + 6 = 24 + 6 = 30 3 • 10 + 2 = 30 + 2 = 32 2 • 5 + 2 = 10 + 2 = 12 |