
Завдання 1050
Познач на координатній прямій точки А(–5), В(2), С(–2), М(–6), К(4). Знайди модулі координат цих точок.

Модуль кооринати А: |–5| = 5
Модуль кооринати В: |2|= 2
Модуль кооринати С: |–2| = 2
Модуль кооринати М: |–6| = 6
Модуль кооринати К: |4| = 4
Завдання 1051
Познач на координатній прямій точки А(–5), В(1), С(–3), М(–7), Р(9) та точки, що мають протилежні координати.
Завдання 1052
Познач на координатній прямій точки А(–2) і В(8) та точку С — середину відрізка АВ.
Середина відрізка АВ точка С(3)
Завдання 1053
Познач на координатній прямій цілі числа, які задовольняють нерівність:
а) –3 < x < 7, цілі числа х = –2, –1, 0 , 1, 2, 3, 4, 5, 6
б) –8 < x < –5; цілі числа х = –7, –6
в) −4 ≤ х ≤ 3. x; цілі числа: х = –4, –3, –2, –1, 0 , 1, 2, 3

Завдання 1054
Побудуй трикутник АВС, якщо А(–5;–2), В(3; 4), С(6; –2).
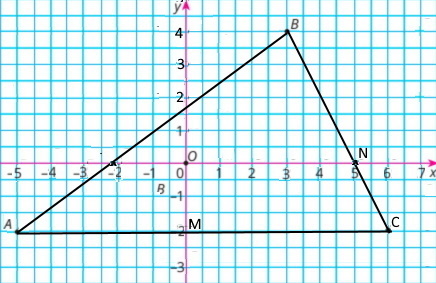
а) координата точки перетину відрізка ВС з віссю абсцис: N(5;0)
б) координата точки перетину відрізка АС з віссю ординат: M(0;–2)
Завдання 1055
Побудуй чотирикутник АВМК, якщо А(–2; 0), В(–5; 2), М(1; 3), К(3; 0).
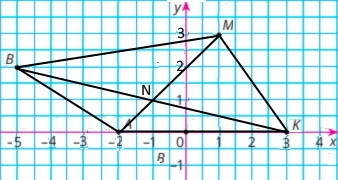
Координати точки перетину відрізків АМ і ВК: N(–1;1)
Завдання 1056
Побудуй точки А(–4; 3) і С(–4; –2) та точки К і Р такі, щоб чотирикутник АСКР був:
а) квадратом;

б) прямокутником.

Завдання 1057
а) –3 < c < 4; цілі числа с = –2, –1, 0, 1, 2, 3
б) –10 < y < –3; цілі числа с = –9, –8, –7, –6, –5, –4
в) −5 ≤ х < –1; цілі числа с = –5, –4, –3, –2
г) −2 ≤ а ≤ 2; цілі числа с = а = –2, –1, 0, 1, 2
Завдання 1057 Модуль числа
а) |-56| : 8 – |–3| • |2| = 56 : 8 – 3 • 2 = 7 – 6 = 1
в) (62 : |–2| – |6|) • |–4| = (62 : 2 – 6) • 4 =(31 – 6) • 4 = 25 • 4 = 100
б) 72 : |–12| + |–4| = 72 : 12 + 4 = 6 + 4 = 10
г) |–168| : (36 • |5| – |–1872| : |–12|) = 168 : (36 • 5 – 1872 : 12) =
= 168 : (180 – 156) = 168 : 24 = 7
Завдання 1059 Рівняння
а) |x| = 5, х = 5 або х = −5
б) |x| = 178; х = 178 або х = −178
в) |x| = 0; х = 0
г) |x| = –12; Рівняння не має розв'язків
ґ) |x| + 7 = 16; |x| = 16 − 7; |x| = 9; х = 9 або х = −9
д) |x| – 8 = 9; |x| = 9 + 8; |x| = 17: х = 17 або х = –17
е) |x| + 8 = 6; |x| = 6 − 8; |x| = −2. Рівняння не має розв'язків
є) 2|х| – 3 = 15; 2|х|= 15 + 3; 2|х|= 18; |х| = 18 : 2; |х|= 9; х = 9 або х = –9
Завдання 1050
Знайди суму усіх цілих значень х, які задовольняють нерівність:
а) |x| < 5; −5 < x < 5, х = −4; −3; −2; −1; 0; 1; 2; 3; 4
−4 + (−3) + (−2) + (−1) + 0 + 1 + 2 + 3 + 4 = 0
б) |x| ≤ 6; −6 ≤ x ≤ 6, х = −6; −5; −4; −3; −2; −1; −0; 1; 2; 3; 4; 5; 6
−6 + (−5) + (−4) + (−3) + (−2) + (−1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 = 0
Завдання 1061 Порівняня чисел
|
–5 < 2 |
6 > –12 |
–3 > –4 |
126 > –324 |
–17 < 0 |
|−3| = |3| |
|−34| > –2 |
Завдання 1062
|
а) –23 + 16 = –7
–7 + (–9) = –16
15 – (–5) = 20
–8 – 6 = –14
–15 – (–18) = 3
|
б) 64 – 72 = –8
–18 + (–42) = –60
84 + (–48) = 36
–45 – (–65) = 20
–127 + 33 = –94
|
в) –6 • 12 = –72
42 • (–10) = –420
–6 • (–5) = 30
–17 • (–15) = 255
84 • (–4) = –336
|
г) –68 : 2 = –34
32 : (–16) = –2
–44 : (–4) = 11
–126 : 18 = –7
–138 : (–23) = 6
|
Завдання 1063 Не виконуючи обчислень, порівняй значення виразів:
|
(–3)2 > (–8)3
|
24 = (–2)4
|
0 > (–6)3
|
0 < (–6)2
|
–53 = (–5)3
|
Завдання 1064 Розкрий дужки та спрости вираз:
а) 2(а + b) + 3(a – 2b) = 2a + 2b + 3a – 6b = 5a – 4b
б) 6(x – 2y) – 2(3x + y) = 6x – 12y – 6x – 2y = –14y
в) (x + 3y – 2) + (2x – 3y + 6) = x + 3y – 2 + 2x – 3y + 6 = 3x + 4
г) –5(a + 2b – 3c) – 2(3a – 5b) = –5a –10b + 15c –6a + 10b = 15c – 11a
ґ) (2x + 5y) – 2(x + y – 3z) = 2x + 5y – 2x – 2y + 6z = 3y + 6z
д) 7a – 3(2a – 4b) – 12b = 7a – 6a + 12b – 12b = a
e) 17 + 3(4x – 5y) –(12x + 15y + 7) = 17 + 12x – 15y – 12x –15y – 7 = 10 – 30y
є) (a + b + c) – (a + b) + (a – c) = a + b + c – a – b + a – c = a
Завдання 1065
|
а) –3х + 7 = –2
3х = 7 + 2
3х = 9
х = 9 : 3
х = 3
|
в) –3х – 6х = –18
–9х = –18
х = –18 : (–9)
х = 2
|
ґ) 68 – (–7х – 12) = 108
68 + 7х + 12 = 108
7х = 108 – 12 – 68
7х = 28
х = 28 : 7
х = 4
|
|
б) 2х – 14 = –6;
2х = –6 + 14
2х = 8
х = 8 : 2
х = 4
|
г) 2х + 6х = –48
8х = –48
х = –48 : 8
х = –6
|
д) –(3 – 5х) – 2х + 28 = –5
–3 + 5х – 2х + 28 = –5
3х + 25 = –5
3х = –5 - 25
3х = –30
х = –30 : 3
х = –10
|
Завдання 1066
а) –46 : (–2) + (–38) • 8 + (–9)2 = 23 – 304 + 81 = –200
б) 255 : (–17) – 15 • (–18) – (–135) : (–9) = –15 + 270 – 15 = 240
в) 27 • (–12) + 464 : (–58) – 512 : (–16) = –324 – 8 + 32 = –332 + 32 = –300
г) –48 • (92 – 158) – (–1885) : (479 – 544) + (–139) = –4416 + 7584 – 29 – 139 =
= 3168 – 29 – 139 = = 3000
ґ) (1625 + 113 • (–13)) : (–12) – 325 : (–25) = (1625 –1469) : (–12) + 13 =
= 156 : (–12) + 13 = –13 + 13 = 0
д) (475 – 574) : 11 – (–189 – 116) : (–61) = –99 : 11 – (–305) : (–61) = –9 – 5 = –4
Завдання 1067
а) ділиться на 3 найбільше і найменше чотирицифрове число: 9999 і 1002
б) ділиться на 5 найбільше і найменше чотирицифрове число: 9995 і 1000
в) ділиться на 3 і на 5 найбільше і найменше чотирицифрове число: 9990 і 1005
Завдання 1068
|
а) на 2 ділиться число 3520
б) на 5 ділиться число 3520
|
в) на 9 ділиться число 3528
г) на 15 ділиться число 3525
|
Завдання 1069
Потрібно дописати зліва до числа 1234 можливу цифру, щоб ділилося:
|
а) на 2; 11234
|
б) на 3; 2234
|
в) на 5; Не можливо
|
а) на 2; 11234
|
Завдання 1070 Ознаки подільності чисел
Які цифри можна записати замість * у числі 52*34*, щоб отримане число ділилося:
а) діляться на 5 числа: 520340; 521340; 522340; 523340; 524340; 525340; 526340; 527340; 528340; 529340; 520345; 521345; 522345; 523345; 524345; 525345; 526345; 527345; 528345; 529345
б) діляться на 9 числа: 520344; 521343; 522342; 524340
в) ділиться на 5 і на 9 число 524340
Завдання 1071
Усі дільники числа 12: 1; 2; 3; 6; 12
Усі дільники числа 15: 1; 3; 5; 15
Усі дільники числа 28: 1; 2; 4; 7; 14; 28
Усі дільники числа 74: 1; 2; 37; 74
Усі дільники числа 1155: 1; 3; 5; 7; 11; 15; 21; 33; 35; 55; 77; 105; 165; 231; 385; 1155
Найбільше дільників має число 1155.
Завдання 1072
Всі прості числа, які задовольняють нерівність:
|
а) 6 < x < 14, х = 7; 11; 13
б) 12 < a < 21, х = 13; 17; 19
|
в) 1 ≤ х ≤ 13, х = 1; 2; 3; 5; 7; 11
г) 0 ≤ а < 11, х = 1; 2; 3; 5; 7
|
Завдання 1073 Розклад на прості множники
|
18 = 2 • 3 • 3
108 = 2 • 2 • 3 • 3 • 3
144 = 2 • 2 • 2 • 2 • 3 • 3
|
180 = 2 • 2 • 3 • 3 • 5
1776 = 2 • 2 • 2 • 2 • 3 • 37
6468 = 2 • 2 • 3 • 7 • 7 • 11
|
Завдання 1074 Взаємно прості числа
|
а) 54 і 75; Ні
54 = 2 • 3 • 3 • 3
75 = 3 • 5 • 5
НСД(54;75) = 3
|
б) 46 і 85; Так
46 = 2 • 23
85 = 5 • 17
НСД(46;85) = 1
|
в) 574 і 615; Ні
574 = 2 • 7 • 41
615 = 3 • 5 • 41
НСД(574;615) = 41
|
г) 216 і 275. Так
216 = 2 • 2 • 2 • 3 • 3 • 3
275 = 5 • 5 • 11
НСД(216;275) = 1
|
Завдання 1074
|
б) 46 і 85; Так
46 = 2 • 23
85 = 5 • 17
НСД(46;85) = 1
|
г) 216 і 275. Так
216 = 2 • 2 • 2 • 3 • 3 • 3
275 = 5 • 5 • 11
НСД(216;275) = 1
|
Завдання 1075
Числа 13 780 і і 6254 не є взаємно простими, бо мають більше, ніж два дільники.
Числа 4857 і 16 497 є взаємно простими, бо мають тільки два дільники.
|
а) 24 і 18;
24 = 2 • 2 • 2 • 3
18 = 2 • 3 • 3
НСД(24;18) = 2•3 = 6
НСК(24; 18) = 2•2•2•3•3 = 72
|
в) 88 і 56;
88 = 2 • 2 • 2 • 11
56 = 2 • 2 • 2 • 7 = 616
НСД(88;56) = 2•2•2 = 8
НСК(24; 18) = 2•2•2•11•7 = 616
|
|
б) 14 і 63;
14 = 2 • 7
63 = 3 • 3 • 7
НСД(14;63) = 7
НСК(14; 65) = 3•3•7•2 = 126
|
г) 128 і 320.
128 = 2 • 2 • 2 • 2 • 2 • 2 • 2
320 = 2 • 2 • 2 • 2 • 2 • 2 • 5
НСД(128;320) = 2•2•2•2•2•2 = 64
НСК(128;320) = 2•2•2•2•2•2•2•5 = 640
|
Завдання 1077
Між учнями класу розділили порівну 120 зошитів і 72 олівці. Скільки учнів у класі?
Розв'язання
120 = 2 • 2 • 2 • 3 • 5
72 = 2 • 2 • 2 • 3
НСД(120;72) = 2 • 2 • 2 • 3 = 24
Відповідь: у класі 24 учні.
Завдання 1078
Три автобуси вийшли на маршрути одночасно. Один із них виконує рейс за 12 годин, другий — за 14 год, а третій — за 16 годин. Через скільки днів усі три автобуси зустрінуться знову на цьому ж місці?
Розв'язання
12 = 2 • 2 • 3
14 = 2 • 7
16 = 2 • 2 • 2 • 2
НСК(12;14;16) = 2 • 2 • 2 • 2 • 3 • 7 = 336
Відповідь: через 336 годин усі три автобуси зустрінуться знову на цьому ж місці.
Завдання 1079 Порівняня дробів
а) 2/3 = 10/15, 3/5 = 9/15, 10/15 > 9/15, тому 2/3 > 3/5
б) 3/8 = 21/56, 2/7 = 16/56, 21/56 > 16/56, тому 3/8 > 2/7
в) 4/9 = 28/63, 3/7 = 27/63, 28/63 > 27/63, тому 4/9 > 3/7
г) 5/17 = 35/119, 2/7 = 34/119, 35/119 > 34/119, тому 5/17 > 2/7
Завдання 1080
3/5 = 36/60; 13/13 = 1; 7/12 = 35/60; 2/3 = 40/60; 11/6 = 110/60; 1/2 = 30/60
У порядку зростання числа: 1/2; 7/12; 3/5; 2/3; 13/13; 11/6
Завдання 1081
а) 15•26/13•10•8 = 3•2/2•8 = 3/8
б) 36•17•32/8•51•16 = 9•1•2/2•3•1 = 3
в) 12•13•13•18/15•40•15•14 = 13(12+18)/15(40-14) = 13•30/15•26 = 2/2 = 1
Завдання 1082 Додавання дробів
Запиши десяткові дроби у вигляді звичайних дробів і виконай дії:
а) 0,4 + 5/12 = 4/10 + 5/12 = 2/5 + 5/12 = 24/60 + 25/60 = 49/60
б) 7/20 + 1,05 = 7/20 + 1 5/100 = 35/100 + 1 5/100 = 1 40/100 = 1 2/5
в) 5,3 – 2 1/5 = 5 3/10 – 2 1/5 = 5 3/10 – 2 2/10 = 3 1/10
г) 0,6 + 1 2/5 – 1 4/7 = 6/10 + 1 2/5 – 1 4/7 = 3/5 + 1 2/5 – 1 4/7 = 2 – 1 4/7 = 3/7
Завдання 1083 Виконай дії у десяткових дробах:
|
а) 1/4 + 3,75 = 0,25 + 3,75 = 4
б) 2,85 – 7/20 = 2,85 – 0,35 = 2,5
|
в) 5,38 + 3/25 = 5,38 + 0,12 = 5,5
г) 5 1/5 + 2,8 = 5,2 + 2,8 = 8
|
Завдання 1084
|
а) 2/3 + х = 2 3/4
х = 2 3/4 – 2/3
х = 2 9/12 – 8/12
х = 2 1/12
|
в) 2 3/5х – 1 5/6 = 1/3
2 3/5х – 1 5/6 = 1/3 + 1 5/6
2 3/5х = 2/6 + 1 5/6
2 3/5х = 2 1/6
х = 13/6 : 13/5
х = 13/6 • 5/3
х = 5/6
|
ґ) 1/2х + 1/3х + 3/4х = 1 4/15
6/12х + 4/12х + 9/12х = 1 4/15
19/12х = 19/15
х = 19/15 : 19/12
х = 19/15 • 12/19
х = 12/15
х = 4/5
|
|
б) 5/9 – х = 1/6
х = 5/9 – 1/6
х = 10/18 – 3/18
х = 7/18
|
г) 6 2/3 – 3 1/7х = 2 4/15
3 1/7х = 6 2/3 – 2 4/15
3 1/7х = 6 10/15 – 2 4/15
3 1/7х = 4 6/15
3 1/7х = 4 2/5
х = 4 2/5 : 3 1/7
х = 22/5 : 22/7
х = 22/5 • 7/22
х = 7/5
х = 1 2/5
|
д) 1/7 (7х + 14) – 2 1/3 = 1 2/3
х + 2 = 1 2/3 + 2 1/3
х + 2 = 4
х = 4 – 2
х = 2
|
Завдання 1085
Мама купила 15 пиріжків. Діти з’їли 2/5 всіх пиріжків, бабуся — 1/3 залишку. Скільки пиріжків залишилося батькам?
Розв'язання
1) 15 • 2/5 = 6 (п.) – з'їли діти;
2) 15 – 6 = 9 (п.) – залишок;
3) 9 • 1/3 = 3 (п.) – з'їла бабуся;
4) 15 – (6 + 3) = 6 (п.) – залишилося пиріжків.
Відповідь: батькам залишилося 6 пиріжків.
Завдання 1086
Одна бригада може виконати виробниче завдання за 12 днів, а друга — за 18 днів. За скільки днів це завдання виконають дві бригади, якщо працюватимуть разом?
Розв'язання
1) 1/12 + 1/18 = 3/36 + 2/36 = 5/36 (д.) – виготовляють деталей разом за 1 день.
2) 1 : 5/36 = 1 • 36/5 = 36/5 = 7,2 (дн.)
Відповідь: за 7,2 дні виконають завдання дві бригади, якщо працюватимуть разом.
Завдання 1087
Швидкість човна 10 5/6 км/год, а швидкість течії на 8 1/3 км/год менша. Човен рухався 3 години за течією річки і 4 години проти течії. Який шлях пройшов човен
Розв'язання
1) 10 5/6 – 8 1/3 = 10 5/6 – 8 2/6 = 2 3/6 = 2 1/2 (км/год) – швидкість течії;
2) 10 5/6 + 2 1/2 = 10 5/6 + 2 3/6 = 12 8/6 = 12 4/3 = 13 1/3 (км/год) – швидкість за течією річки;
3) 13 1/3 • 3 = 40/3 • 3 = 40 ( км) – пройшов за течією річки
4) 10 5/6 – 2 1/2 = 10 5/6 – 2 3/6 = 8 2/6 = 8 1/3 (км/год) – швидкість проти течією річки;
5) 8 1/3 • 4 = 25/3 • 4 = 100/3 = 33 1/3( км) – пройшов проти течії річки.
6) 40 + 33 1/3 = 73 1/3 (км)
Відповідь: човен пройшов 73 1/3 км.
Завдання 1088
Відстань між станціями 560 км. З якою швидкістю рухався поїзд, якщо за 4 години він проїхав 3/7 цієї відстані?
Розв'язання
1) 560 • 3/7 = 80 • 3 = 240 ( км) – проїхав.
2) 240 : 4 = 60 (км/год)
Відповідь: поїзд рухався зі швидкістю 60 км/год.
Завдання 1089
Гострим чи тупим буде кут, який становить 7/12 розгорнутого кута?
Розв'язання
180 • 7/12 = 15 • 7 = 105 (градусів)
Відповідь: тупим буде кут.
Завдання 1090
Ширина прямокутника 52 см, що становить 13/18 його довжини. Знайди периметр і лощу прямокутника.
Розв'язання
1) 52 : 13/18 = 52 • 18/13 = 4 • 18 = 72 (см) – довжина прямокутника;
2) (52 + 72) • 2 = 124 • 2 = 248 (см) – периметр прямокутника;
3) 52 • 72 = 3744 (см²) – площа прямокутника.
Відповідь: 248 см; 3744 см².
Завдання 1091
Фермер привіз у місто 200 кг яблук. До дитячого садка він завіз 7/20 всіх яблук, а до школи — 5/13 залишку. Скільки кілограмів яблук він завіз до садка і скільки до школи? Скільки кілограмів яблук залишилося?
Розв'язання
1) 200 • 7/20 = 70 (кг) – завіз до дитячого садка;
2) 200 – 70 = 130 (кг) – залишок;
3) 130 • 5/13 = 50 (кг) – завіз до школи;
3) 200 – (70 + 50) = 80 (кг) – залишилося яблук.
Відповідь: 70 кг; 130 кг; 80 кг.
Завдання 1092
За перший тиждень робітники виконали 5/12 всього замовлення, а за другий тиждень вони виготовили решту — 140 деталей. Скільки всього деталей виготовили робітники?
Розв'язання
1) 1 – 5/12 = 7/12 – становить решта.
2) 140 : 7/12 = 140 • 12/7 = 20 • 12 = 240 (д.)
Відповідь: робітники виготовили 240 деталей.
Завдання 1093
2/5 своїх грошей Аліса витратила на книжку. Скільки грошей було в Аліси, якщо після покупки книжки у неї залишилося 300 грн? Скільки коштувала книжка?
Розв'язання
1) 1 – 2/5 = 3/5 – становить залишок.
2) 300 : 3/5 = 300 • 5/3 = 500 (грн)
Відповідь: книжка коштувала 500 грн.
Завдання 1094
Автомобіль проїхав 3/8 всієї відстані між містами. Яка відстань між містами, якщо залишилося їхати ще 120 км?
Розв'язання
1) 1 – 3/8 = 5/8 – залишилося проїхати.
2) 120 : 5/8 = 120 • 8/5 = 24 • 8 = 192 (км)
Відповідь: між містами 192 км.