Інші завдання дивись тут ...

© ГДЗ 8next.com, 2013, 2018, 2022

Запитання

1. Що означає поділити число а на число 6? Знайти таке число, добуток якого з числом 6 дорівнює а.

2. Як у рівності а : b = с називають число а? число b? число с? запис а : b? У рівності а : b = с число а називають діленим, число Ь — дільником, число с і запис а : b — часткою.

3. Що показує частка двох чисел? Частка а : b показує, у скільки разів число а більше за число b або у скільки разів число b менше від числа а.

4. На яке число ділити не можна? На нуль ділити не можна.

5. Чому дорівнює частка від ділення числа 0 на будь-яке натуральне число? 0 : а = 0

6. Чому дорівнює частка а : а, де а ≠ 0? а : а = 1

7. Чому дорівнює частка а : 1? а : 1 = а

8. Як знайти невідомий множник? Правило знаходження невідомого множника: щоб знайти невідомий множник, треба добуток поділити на відомий множник.

9. Як знайти невідоме ділене? Правило знаходження невідомого діленого: щоб знайти невідоме ділене, треба дільник помножити на частку.

10. Як знайти невідомий дільник? Правило знаходження невідомого дільника: щоб знайти невідомий дільник, треба ділене поділити на частку.

 

Розв’язуємо усно

Завдання 1 Заповніть ланцюжок обчислень.

Завдання 2 Виконай ділення

1) 432 : 4 = (400 + 32) : 4 = 400 : 4 + 32 : 4 = 100 + 8 = 108

2) 609 : 3 = (600 + 9) : 3 = 600 : 3 + 9 : 3 = 200 + 3 = 203

3) 3600 : 6 = 600

4) 1500 : 50 = 30

 

Завдання 3 Укажіть серед даних добутків найбільший:

1) 239 • 4 • 25 = 239 • 100

2) 239 • 20 • 4 =  239 • 80

3) 10 • 239 • 10 = 239 • 100

4) 239 • 10 • 12 = 239 • 120 – найбільший добуток

 

Завдання 4 Доганяючи Сашка, Славко біжить зі швидкістю 180 м/хв. Чому дорівнює швидкість Сашка, якщо хлопчики зближуються зі швидкістю 12 м/хв?

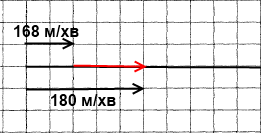
Розв'язання

180 – 12 = 168 (м/хв)

Відповідь: швидкість Сашка 168 м/хв.

 

Завдання 5 Два автомобілі рухаються назустріч один одному, причому один із них зі швидкістю 74 км/год. Чому дорівнює швидкість другого автомобіля, якщо вони зближуються зі швидкістю 150 км/год?

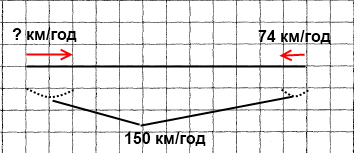
Розв'язання

150 – 74 = 76 (км/год) – швидкість другого автомобіля.

Відповідь: швидкість другого автомобіля дорівнює 76 км/год.

 

Завдання 6

Щоб бути здоровою, людина щодня має споживати 3 г білка на кожні 4 кг своєї маси. Скільки грамів білка має отримувати на день дитина, маса якої становить 36 кг?

Розв’язання

1) 36 : 4 = 9 (разів) – у стільки разів більше білка має отримувати.

2) 3 • 9 = 27 (г) – білка має отримувати на день дитина.

Відповідь: 27 грамів білка має отримувати на день дитина.

 

Вправи

Завдання 479° Відомо, що 243 • 425 = 103 275. Чому дорівнює значення виразу:

1) 103275 : 243 = 243 • 425 : 243 = 243 : 243 • 425 = 1 • 425 = 425

2) 103275 : 425 = 243 • 425 : 425 = 243 • 1 = 243

 

Завдання 480° Відомо, що 4608 : 48 = 96. Чому дорівнює значення виразу:

1) 96 • 48 = 4608

2) 4608 : 96 = 4608 : (48 • 2) = 4608 : 48 : 2 = 96 : 2 = 48

 

Завдання 481° Заповніть таблицю

Ділене	320	96	84	0	0	945	637	3232
Дільник	40	12	6	264	128	1	637	16
Частка	8	8	14	0	0	945	1	202

Завдання 482° Письмове ділення

1) _1548 | 36   144     43   _108     108        0	2) _5562 | 18    54       309   _162     162        0	3) _15552 | 72    144       216    _115      72     _432       432          0
4) _16320 | 48     144      340   _192     192         0	5) _906192 | 126     882         7192   _241     126    _1159      1134        _252          252             0	6) _2430000 | 1800    1800          1350   _6300     5400     _9000       9000            0

Завдання 483°

1) _2812 | 74    222      38  _592    592       0	2) _9384 | 46     92       204  _18     0  _184    184       0	3) _18526 | 59    177       314    _82      59     _236       236          0
4) _63378 | 63      63          1006     _378       378          0	5) _153216 | 38       152        4032     _121        114         _76           76             0	6) _1334504 | 214      1284         6236     _505       428        _770          642         _1284           1284                0

Завдання 484° Знайдіть частку та зробіть перевірку письмовим множенням:

_16728 | 68    136      246   _312     272     _408       408          0

Перевірка: х 246     68  1968 1476   16728

_942866 | 178     890       5297   _528     356    _1726      1602      _1246        1246             0

Перевірка: х 5297     178  42376 37079 5297   942866

Завдання 485°

_1248 | 24    120     52     _48       48         0

Перевірка: х 52    24  208 104   1248

_15652 | 26     156      602       _52          52           0

Перевірка: х 602     26  3612 1204   15652

Завдання 486° У скільки разів одна величина більша за другу:

1) 1 т і 100 кг;  У 10 разів  (1000 кг : 100 кг = 10)

3) 24 ц і 8 кг;  У 30 разів   (240 кг : 8 кг = 30)

2) 20 см і 1 м;  У 10 разів   (100 см : 20 см = 5)

4) 10 хв і 2 год?  У 12 разів  (120 х : 10 хв = 12)

 

Завдання 487° У скільки разів одна величина менша від другої:

1) 1 км і 250 м;  У 4 рази  (1000 м : 250 кг = 4)

2) 4 ц і 2 т;  У 5 разів  (20 кг : 4 ц = 5)

3) 3 хв і 3 с?  У 60 разів  (180 с : 3 с = 60)

 

Завдання 488° (Домашня практична робота) У записі 339 968 : 32 = ВУЖЙІ буквами позначено цифри числа, що є результатом ділення. Із цих букв складається прізвище видатної української акторки. Щоб розшифрувати слово, достатньо в наведеній таблиці під кожною цифрою записати літеру, яка стоїть на місті цієї цифри в правій частині даного запису. Установіть прізвище мисткині.

_339968 | 32        32         10624   _199     192      _76        64       _128         128            0
0	6	1	4	2
У	Ж	В	І	Й

Завдання 489° Знайдіть значення виразу:

 

Завдання 492° Розв'яжіть рівняння

1) 13х = 195     х = 195 : 13      х = 15		2) х • 18 = 468     х = 468 : 18     х = 26	3) 11х + 6х = 408     17 х = 408     х = 408 : 17     х = 24
_195 | 13   13     15   _65     65       0		_468 | 18     36      26  _108    108       0	_408 | 17     34      24     68      68        0
4) 33m – m = 1024     32m= 1024     m = 1024 : 32     m = 32		5) х : 19 = 26     х = 26 • 19     х = 494	6) 476 : х = 14     х = 476 : 14     х = 34
_1024 | 32    96     32    _64      64        0		х 26   19 234 26   494	_476 | 14    42     34   _56     56        0

Завдання 493°

1) 19х = 95     х = 95 : 19     х = 5		2) х • 22 = 132     х = 132 : 22     х = 6	3) 38х – 16х = 1474     22х = 1474     х = 1474 : 22     х = 67
_95 | 19   95    5     0		_132 | 22     132    6      0	_1474 | 22     132     67   _154     154        0
4) у + 27у = 952     28у = 952     у = 952 : 28     у = 34		5) х : 25 = 16     х = 16 • 25     х = 400	6) 324 : х = 27     х = 324 : 27     х = 12
_952 | 28     84      34 _112   112      0		х 16    25   80  32     400	_324 | 27    27     12   _54     54       0

Завдання 494 Замість одного дерева в паперовій промисловості можна використати 60 кг макулатури. Скільки дерев урятують учні школи, у якій навчається 520 школярів, якщо кожний із них здасть 3 кг макулатури?

Розв’язання

1) 3 • 520 = 1560 (кг) – всього макулатури зберуть учні.

2) 1560 : 60 = 26 (д.) – дерев урятують учні школи.

Відповідь: 26 дерев урятують учні школи.

 

Завдання 495 Вершник долає відстань між двома селищами за 5 год, якщо рухається зі швидкістю 12 км/год. З якою швидкістю він має рухатися, щоб подолати цю відстань за 4 год?

Розв'язання

1) 12 • 5 = 60 (км) – відстань між селищами.

2) 60 : 4 = (40 + 20) : 4 = 15 (км/год) – нова швидкість вершника.

Відповідь: вершник повинен рухатися зі швидкістю 15 км/год.

 

Завдання 496

Купили 8 кг печива за ціною 72 грн за кілограм. Скільки кілограмів печива за ціною 48 грн за кілограм можна купити за ці самі гроші?

Розв’язання

1) 72 • 8 = 576 (грн.) – вартість покупки.

2) 576 : 48 = 12 (кг) – печива за ціною 48 грн можна купити.

Відповідь: 12 кілограмів печива за ціною 48 грн можна купити.

 

Завдання 497 Порядок дій

1 ) 82 275 - 64 • 56 + 9680 : 16 - 23 637 = 55659
х   64     56   384  320    3584	_9680 | 16     96        605    _80      80        0	_82275     3584   78691	+ 78691       605    79296	_79296   23637   55659
2) (204 • 402 - З0 456 : 423) : 36 - 1388 = 888
х  204    402    408 816    82008	_30456 | 423  2961      72    _846      846         0	_82008       72   81936	_81936 | 36      72         2276  _99    72   _273     252     _216       216          0	_2276   1388     888

Завдання 498 

1) 49 184 + 4575 : 15 - 62 • 93 - 33 999 = 9724
_4575 | 15   45     305   _75     75       0	х 62    93  186 558   5766	+ 49184       305    49489	_49489    5766   43723	_43723   33999    9724
3) 1885 : (542 - 477) + 48 • (134 - 92) = 2045
_ 542    477     65	_134    92    42	_1885 | 65  130     29  _585    585       0	х   42     48    336  168    2016	+2016      29   2045

Завдання 499 Малюк купив для Карлсона 8 тістечок і 12 булочок з повидлом, заплативши за всю покупку 408 крон. Одне тістечко коштує 24 крони. Скільки коштує одна булочка?

^{Короткий запис}

^{Вартість — 24 408 кр.} 

^{Тістечка — ?, 8 шт. по 24 кр.}

^{Булочки — 12 шт. по ? кр.}

Розв'язання

1) 24 • 8 = (20 + 4) • 8 = 192 (кр.) – заплатив за тістечка.

2) 408 – 192 = 216 (кр.) – заплатив за булочки.

3) 216 : 12 = 216 : 2 : 6 = 18 (кр.) – ціна булочки.

Відповідь: одна булочка коштує 18 крон. 

 

Завдання 500 Дід Панас заготовив на зиму 6 діжок квашеної капусти і 14 діжок солоних огірків. В одну діжку вміщується 26 кг капусти. Скільки кілограмів огірків міститься в одній діжці, якщо всього дід Панас заготовив 324 кг овочів?

^{Короткий запис}

^{Овочів — 324 кг}

^{Капусти — ?, 6 д. по 26 кг}

^{Огірків — 14 д. по ? кк}

Розв'язання

1) 26 • 6 = 156 (кг) – квашеної капусти заготовив.

2) 324 – 156 = 168 (кг) – солоних огірків заготовив.

3) 168 : 14 = 168 : 2 : 7 = 12 (кг) – огірків у одній діжці.

Відповідь: у одній бочці 12 кг огірків.  

 

Завдання 501 Скільки кілограмів масла можна виготовити з 261 кг вершків, якщо з 9 кг вершків отримують 2 кг масла?

^{Короткий запис}

^{261 кг – ? кг}

^{9 кг – 2 кг}

Розв'язання

1) 261 : 9 = 29 (разів) – у стільки разів більше вершків.

2) 2 • 29 = 58 (кг) – масла можна отримати.

Відповідь: з 261 кг вершків можна отримати 58 кг масла.

 

Завдання 502 Курочка Ряба зібрала 328 кг проса. Скільки пшона вона зможе отримати із цього проса, якщо з 4 кг проса виходить 3 кг пшона?

^{Короткий запис}

^{328 кг – ? кг}

^{4 кг – 3 кг}

Розв'язання

1) 328 : 4 = 82 (разів) – у стільки разів більше проса.

2) 3 • 82 = 246 (кг) – пшона зможе отримати.

Відповідь: зможе отримати 246 кг пшона.

 

Завдання 503 Відстань між двома пристанями дорівнює 476 км. Рухаючись за течією річки, катер проходить цю відстань за 14 год. За скільки годин він пройде цю відстань проти течії річки, якщо швидкість течії дорівнює 3 км/год?

Розв'язання

1) 476 : 14 = 34 (км/год) – швидкість катера за течією річки

2) 34 - 3 = 31 (км/год) – власна швидкість катера.

3) 31 - 3 = 28 (км/год) – швидкість катера проти течії річки

4) 476 : 28 = 17 (год) – часу треба.

Відповідь: проти течії річки катер пройде відстань за 17 годин. 

 

Завдання 504 Відстань між двома портами дорівнює 504 км. Рухаючись проти течії річки, теплохід проходить цю відстань за 21 год. За скільки годин він пройде цю відстань за течією річки, якщо швидкість течії дорівнює 2 км/год?

Розв'язання

1) 504 : 21 = 24 (км/год) – швидкість теплохода проти течії річки

2) 24 + 2 = 26 (км/год) – власна швидкість теплохода.

3) 26 + 2 = 28 (км/год) – швидкість за течією річки

4) 504 : 28 = 18 (год) – часу треба.

Відповідь: за течією річки теплохід пройде цю відстань за 18 годин.

 

Завдання 505 Із сіл Квіткове і Казкове, відстань між якими дорівнює 136 км, виїхали одночасно назустріч один одному козаки Шибайголова та Гострошабленко. Шибайголова рухався зі швидкістю 16 км/год. З якою швидкістю їхав Гострошабленко, якщо козаки зустрілися через 4 год після виїзду?

Розв'язання

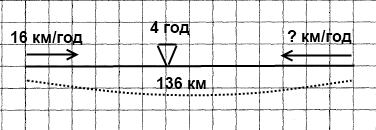
1) 136 : 4 = 34 (км/год) – швидкість зближення.

2) 34 - 16 = 18 (км/год) – швидкість Гострошабенка.

Відповідь: Гострошабенко їхав зі швидкістю 18 км/год.

 

Завдання 506 Відстань між двома містами дорівнює 1264 милі. Із них одночасно вилетіли  назустріч один одному два килими-літаки й зустрілися через 8 год після вильоту. Один із килимів пролітав 82 милі за годину. З якою швидкістю летів другий килим? (1 сухопутна миля = 1609 м)

Розв'язання

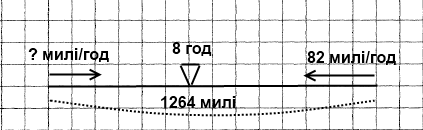
1) 1264 : 8 = 158 (милі/год) – швидкість зближення.

2) 158 - 82 = 76 (милі/год) – швидкість другого килима.

Відповідь: другий килим летів зі швидкістю 76 милі/год.

 

Завдання 507 Із двох станцій, відстань між якими дорівнює 24 км, одночасно в одному напрямі вийшли два поїзди. Попереду йшов поїзд зі швидкістю 58 км/год. Через 4 год після початку руху його наздогнав другий поїзд. Знайдіть швидкість другого поїзда.

Розв'язання

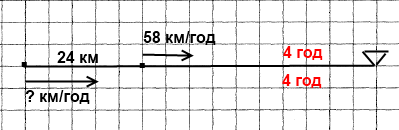
1) 58 • 4 = 232 (км) – відстань першого поїзда.

2) 232 + 24 = 256 (км) – відстань другого поїзда.

3) 256 : 4 = 64 (км/год) – швидкість другого поїзда.

Відповідь: швидкість другого поїзда 64 км/год.

 

Завдання 508 Відстань між селами Вишневе та Яблуневе дорівнює 15 км. Із цих сіл одночасно в одному напрямі вирушили Марина й Дарина. Марина їхала верхи зі швидкістю 9 км/год і через 3 год після початку руху наздогнав Дарину, який йшла пішки. З якою швидкістю йшла Дарина?

Розв'язання

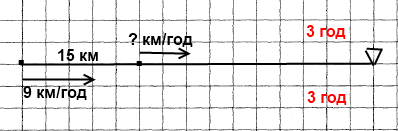
1) 9 • 3 = 27 (км) – відстань проїхала верхи Марина.

2) 27 – 15 = 12 (км) – відстань пройшkа Дарина.

3) 12 : 3 = 4 (км/год) – швидкість Дарини.

Відповідь: Дарина йшла зі швидкістю 4 км/год.

 

Завдання 509 Відстань між містечками Сен-Жермен і Сен-Антуан дорівнює 12 льє. Із цих містечок одночасно в одному напрямі виїхали Портос зі швидкістю 1 льє/год і д’Артаньян зі швидкістю 3 льє/год, причому Портос рухався попереду. Через скільки годин після виїзду д’Артаньян наздогнав Портоса? 

^{Льє — старовинна французька одиниця довжини (1 льє приблизно дорівнює 4444 м).}

Розв'язання

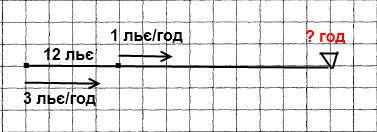
1) 3 – 1 = 2 (льє/год) – швидкість зближення. 

2) 12 : 2 = 6 (год) – через стільки годин наздожене.

Відповідь: д’Артаньян наздогнав Портоса через 6 год.

 

Завдання 510 Відстань між островами Акулячий і Китовий дорівнює 48 морських миль. Від цих островів одночасно в одному напрямі вирушили фрегати ≪Відважний ≫ і ≪Стрімкий≫, причому ≪Відважний≫ ішов попереду ≪Стрімкого≫. ≪Відважний≫ проходив за годину 12 миль, а ≪Стрімкий≫ — 18 миль. Через скільки годин ≪Стрімкий≫ наздогнав ≪Відважного≫?

^{1 морська миля = 1852 м.}

Розв'язання

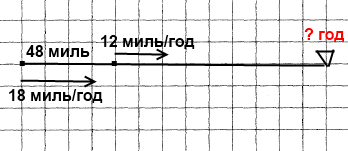
1) 18 – 12 = 6 (миль/год) – швидкість зближення.

2) 48 : 6 = 8 (год) – через стільки годин наздожене.

Відповідь: ≪Стрімкий≫ наздогнав ≪Відважного≫ через 8 год.

 

Завдання 511* Мальвіна живе на відстані 1 км 200 м від школи. Уроки в школі починаються о 8 год 30 хв. Мальвіна робить за хвилину 120 кроків, довжина кроку — 40 см. О котрій годині вона має виходити з дому, щоб приходити до школи за 10 хв до початку занять?

Розв'язання

1) 120 • 40 = 4800 (см) = 48 (м) – відстань проходить за 1 хв.

2) 1200 : 48 = 25 (хв) – час руху до школи.

3) 8 год 30 хв – 10 хв = 8 год 20 хв – час приходу до школи.

4) 8 год 20 хв – 25 хв = 7 год + 80 хв – 25 хв = 7 год  + 55 хв = 7 год 55 хв

Відповідь: Мальвіна має виходити з дому о 7 год 55 хв. 

 

Завдання 512* Чергові першого загону туристів за 6 хв можуть почистити 24 картоплини, а чергові другого загону за 9 хв — 45 картоплин. За скільки хвилин спільної роботи вони почистять 198 картоплин?

^{Короткий запис}

^{I — 6 хв — 24 к.}

^{II — 9 хв — 43 к.}

^{Разом — ? хв — 198 к.}

Розв'язання

1) 24 : 6 = 4 (к.) – картоплин чистять чергові першого загону за 1 хв.

2) 45 : 9 = 5 (к.) – картоплин чистять чергові другого загону за 1 хв.

3) 4 + 5 = 9 (к.) – картоплин чистять чергові двох загонів разом за 1 хв.

4) 198 : 9 = 22 (хв) – потрібно часу.

Відповідь: 198 картоплин вони почистять за 22 хв спільної роботи. 

 

Завдання 513 На скільки днів шкільній їдальні вистачить 800 л соку, якщо хлопчики за 8 днів випивають 960 л соку, а дівчатка за 6 днів — 480 л?

^{Короткий запис}

^{Хлопчики — 8 дн. — 960 л}

^{Дівчатка — 6 дн. — 460 л}

^{Разом — ? дн — 800 л}

Розв'язання

1) 960 : 8 = 120 (л) – соку випивають хлопці за 1 день.

2) 480 : 6 = 80 (л) – соку випивають дівчата за 1 день.

3) 120 + 80 = 200 (л) – соку випивають хлопці та дівчата разом за 1 день.

4) 800 : 200 = 4 (дні) – вистачить соку.

Відповідь: соку вистачить на 4 дні. 

 

Завдання 514 За 4 дні роботи три оператори набрали на комп’ютері разом 288 сторінок. Скільки сторінок набере один оператор за 7 днів, якщо в них однакова продуктивність праці?

^{Короткий запис}

^{3 оп., 4 дн. —  288 с.}

^{1 оп., 7 дн. — ?}

Розв'язання

1) 288 : 4 : 3 = 24 (с.) – сторінок набере 1 оператор за 1 день.

2) 24 • 7 = 168 (с.) – сторінок набере 1 оператор за 7 днів.

Відповідь: за 7 днів оператор набере 168 сторінок.

 

Завдання 515 Для роботи 6 однакових двигунів протягом 8 год потрібно 672 л палива. На скільки годин роботи вистачить одному такому двигуну 98 л палива?

^{Короткий запис}

^{6 дв., 672 л — 8 год}

^{1 дв., 98 л — ?}

Розв'язання

1) 672 : 6 : 8 = 14 (л) – палива потрібно для роботи 1 двигуна за 1 год.

2) 98 : 14 = 7 (год) – на стільки часу.

Відповідь: 98 л палива вистачить на 7 год роботи двигуна.

 

Завдання 516 Дід Часник привіз на ринок 420 кг яблук і 180 кг груш у 50 однакових ящиках. Скільки було ящиків з яблуками і скільки — з грушами?

1) 420 + 180 = 600 (кг) – груш і яблук привіз.

2) 600 : 50 = 12 (кг) – маса ящика з фруктами.

3) 420 : 12 = 35 (ящ.) – було ящиків з яблуками.

4) 180 : 12 = 15 (ящ.) – було ящиків з грушами.

Відповідь: було 35 ящиків з яблуками, 15 ящиків з грушами.

 

Завдання 517 Алі-Баба перевозив знайдене в печері розбійників золото на 4 віслюках у 22 однакових мішках. На першого віслюка він навантажив 80 кг золота, на другого — 100 кг, на третього — 120 кг, на четвертого — 140 кг. Скільки мішків золота було навантажено на кожного віслюка?

Розв'язання

1) 80 + 100 + 120 + 140 = 440 (кг) – всього золота.

2) 440 : 22 = 20 (кг) – маса мішка.

3) 80 : 20 = 4 (м.) – мішків навантажено на першого віслюка.

4) 100 : 20 = 5 (м.) – мішків навантажено на другого віслюка.

5) 120 : 20 = 6 (м.) – мішків навантажено на третього віслюка.

6) 140 : 20 = 7 (м.) – мішків навантажено на четвертого віслюка.

Відповідь: на першого віслюка навантажено 4 мішки, на другого - 5 мішків, на третього - 6 мішків, на четвертого - 7 мішків.

 

Завдання 518

1) 21 (18 + х) = 714 18 + х = 714 : 21 18 + х = 34 х = 34 - 18 х = 16 21 • (18 + 16) = 21 • 34 = 714 714 = 714	3) 12 (152 + 19х) = 2052 152 + 19х = 2052 : 12 152 + 19х = 171 19х = 171 - 152 19х = 19 х = 19 : 19 х = 1 12 • (152 + 19 • 1) = 2052 2052 = 2052
_714 | 21     63       34  _84    84      0	_2052 | 12      12       171   _85     84     _12       12         0	_ 171    152      19
2) 16 (4х - 34) = 608 4х - 34 = 608 : 16 4х - 34 = 38 4х = 38 + 34 4х = 72 х = 72 : 4  х = 18 16 • (4 • 18 - 34) = 16 • (72 - 34) = 16 • 38 = 608 608 = 608	4) (152х + 32) • 6 = 192 152х + 32 = 192 : 6  152х  + 32 = 32 152х = 32 - 32  152х = 0 х = 0 : 152 х = 0 (152 • 0 + 32) • 6 = 192 192 = 192
_608 | 16     48       38 _128   128       0	_192 | 6      18     32   _12     12       0

Завдання 519

1) 8 (х - 14) = 56 х - 14 = 56 : 8  х - 14 = 7 х = 7 + 14 х = 21 8 • (21 - 14) = 56 56 = 56	3) 9 (143 - 13х) = 234 143 - 13х = 234 : 9 143 - 13х = 26 13х = 143 - 26 13х = 117 х = 117 : 13 х = 9 9 • (143 - 13 • 9) = 234 234 = 234
2) (46 - х) • 19 = 418 46 - х = 418 : 19 46 - х = 22 х = 46 - 22 х = 24 (46 - 24) • 19 = 418 418 = 418	4) 17 (5х - 16) = 238 5х - 16 = 238 : 17 5х - 16 = 14 5х = 14 + 16 5х = 30 х = 30 : 5  х = 6 17 • (5 • 6 - 16) = 238 238 = 238

Завдання 520 

1) 14 х + 4х - 48 = 240 18 х - 48 = 240 18х = 240 + 48 18х = 288 х = 288 : 18 х = 16	3) 16а – 7а + 96 = 222 9а + 96 = 222 9а = 222 – 96 9а = 126 а = 126 : 9  а = 14
2) 25Ь - 7Ь - 9 = 279 18Ь – 9 = 279 18Ь = 279 + 9 18Ь = 288 Ь = 288 : 18 Ь = 16	4) 20у + 5у + у + 19 = 227. 26у + 19 = 227 26у = 227 – 19 26у = 208 у = 208 : 26 у = 8

Завдання 521 

1) 9Ь + 6Ь – 15 = 615 15Ь – 15 = 615 15Ь = 615 + 15 15Ь = 630 Ь = 630 : 15 Ь  = 42

2) 17х – х + 5х – 19 = 170. 21х – 19 = 170 21х = 170 + 19 21х = 189 х = 189 : 21 х = 9

Завдання 522 

1) (х + 14) : 9 = 13 х + 14 = 13 • 9 х + 14 = 117 х = 117 – 14 х = 103	4) 52 + 72 : х = 56 72 : х = 56 – 52 72 : х = 4 х = 72 : 4 х = (40 + 32) : 4 х = 18
2) 966 : (х + 17) = 23 х + 17 = 966 : 23 х + 17 = 42 х = 42 – 17 х = 25	5) 56 : (х – 6) = 8 х – 6 = 56 : 8 х – 6 = 7 х = 7 + 6 х = 13
3) х : 8 – 6 = 49 х : 8 = 49 + 6 х : 8 = 55 х = 55 • 8 х = 440	6) 56 : х – 6 = 8 56 : х = 8 + 6 56 : х = 14 х = 56 : 14 х = 4

Завдання 523

1) (х – 23) : 26 = 8  х – 23 = 8 • 26 х – 23 = 208 х = 208 + 23 х = 231

2) 1728 : (56 – х) = 36 56 – х = 1728 : 36 56 – х = 48 х = 56 – 48 х = 8

Завдання 524 Батько із сином посадили 108 кущів помідорів, причому батько посадив у 2 рази більше, ніж син. Скільки кущів помідорів посадив син?

Розв'язання

Нехай син посадив х кущів, тоді батько — 2х кущів. Разом вони посадили 108 кущів. Складемо рівняння.

х + 2х = 108

3х = 108

х = 108 : 3

х = (90 + 18) : 3 

х = 36 (к.)

Відповідь: син посадив 36 кущів. 

 

Завдання 525 До двох магазинів завезли 268 кг шампіньйонів, причому до першого магазину завезли шампіньйонів у 3 рази менше, ніж до другого. Скільки кілограмів шампіньйонів завезли до кожного магазину?

Розв'язання

Нехай до першого магазину завезли х кг шампіньйонів, тоді до другого — 3х кг. Разом до двох магазинів завези 268 кг. Складемо рівняння. 

х + 3х = 268

4х = 268

х = 268 : 4

х = (240 + 28) : 4 

х = 67 (кг)

3 • 67 = 201 (кг)

Відповідь: до першого магазину привезли 67 кг грибів, до другого — 201 кг грибів. 

 

Завдання 526 У султана було двогорбих верблюдів у 7 разів більше, ніж одногорбих. Скільки в султана було одногорбих верблюдів, якщо відомо, що їх на 156 менше, ніж двогорбих?

Розв'язання

Нехай одногорбих верблюдів було х, тоді двогорбих — 7х. Складемо рівняння.

7х – х = 156

6х = 156

х = 156 : 6

х = 26 (в.)

Відповідь: у султана було 26 одногорбих верблюдів.

 

Завдання 527 Валентин подарував Валентині троянди й орхідеї, причому орхідей було в 4 рази менше, ніж троянд. Скільки троянд подарував Валентин, якщо відомо, що їх було на 51 більше, ніж орхідей?

Розв'язання

Нехай троянд було х квітів, тоді троянд — 4х квітів. Складемо рівняння.

4х – х = 51

3х = 51

х = 51 : 3

х = 17 (кв.)

4 • 17 = 68 (кв.)

Відповідь: Валентин подарував 68 троянд.

 

Завдання 528 З вершини прямого кута проведено промінь так, що він ділить прямий кут на два кути, один з яких більший за другий на 20°. Знайдіть величину кожного з утворених кутів.

Розв'язання

Нехай величина одного кута х градусів, тоді величина іншого кута х + 20 градусів. Складемо рівняння.

х + (х + 20) = 90

2х + 20 = 90

2х = 90 – 20

2х = 70

х = 70 : 2

х = 35 (°)

35 + 20 = 55 (°)

Відповідь: величина першого кута 35°, другого – 55°.

 

Завдання 529 З вершини розгорнутого кута проведено промінь так, що він ділить розгорнутий кут на два кути, один з яких менший від другого на 50°. Знайдіть величину кожного з утворених кутів.

Розв'язання

Нехай величина одного кута х градусів, тоді величина іншого кута х + 20 градусів. Складемо рівняння.

х + (х + 50) = 180

2х + 50 = 180

2х = 180 – 50

2х = 130

х = 130 : 2

х = 65 (°)

65 + 50 = 115 (°)

Відповідь: величина першого кута 65°, другого – 115°.

 

Завдання 530 На день народження Вінні-Пуху порося П’ятачок, віслюк Іа та кенгуру Кенга подарували 264 кг меду. П’ятачок подарував у 3 рази більше меду, ніж Кенга, а Іа — у 2 рази більше, ніж Кенга. Скільки меду подарував кожен із гостей?

Розв'язання

Нехай х (кг) – меду подарував Кенга, 3х (кг) – меду подарував П’ятачок, 2х (кг) – меду подарував Іа. Складемо рівняння.

х + 3х + 2х = 264

6х = 264

х = 264 : 6

х = (240 + 24) : 6

х = 44 (кг) – меду подарував Кенга.

3х = 3 • 44 = 132 (кг) – меду подарував П’ятачок.  

2х = 2 • 44 = 88 (кг) – меду подарував Іа.

Відповідь: Кенга подарував 44 кг меду, П’ятачок – 132 кг, Іа – 88 кг.

 

Завдання 531 За чотири дні подорожі Сіндбад-мореплавець проплив 546 миль. За другий день він проплив у 4 рази більше, ніж за перший, за третій — у 3 рази більше, ніж за перший, а за четвертий — у 5 разів більше, ніж за перший. Скільки миль пропливав Сіндбад кожного дня?

Розв'язання

Нехай х (миль) – відстань проплив першого дня, 4х (миль) – відстань проплив другого дня, 3х (миль) – відстань проплив третього дня, 5х (миль) – відстань проплив четвертого дня. Складемо рівняння.

х + 4х + 3х + 5х = 546

13х = 546

х = 546 : 13

х = 42 (миль) – відстань проплив першого дня.

4х = 4 • 42 = 168 (миль) – відстань проплив другого дня.

3х = 3 • 42 = 126 (миль) – відстань проплив третього дня.

5х = 5 • 42 = 210 (миль) – відстань проплив четвертого дня.

Відповідь: Синдбад першого дня проплив 42 милі, другого дня – 168 миль, третього дня – 126 (миль), четвертого дня – 210 миль. 

 

Завдання 532 Тарас, Богдан і Олесь зловили 256 окунів. Тарас зловив у 3 рази більше окунів, ніж Богдан, а Олесь — стільки, скільки Тарас і Богдан разом. Скільки окунів зловив найкращий рибалка?

Розв'язання

Нехай х (ок.) – окунів зловив Богдан, 3х (ок.) – окунів зловив Тарас, х + 3х = 4х (ок.) – окунів зловив Олесь. Складемо рівняння.

х + 3х + 4х = 256

8х = 256

х= 256 : 8

х = (240 + 16) : 8

х = 32 (ок.) – окунів зловив Богдан.

4х = 4 • 32 = 128 (ок.) – окунів зловив Олесь.

Відповідь: Олесь зловив 128 окунів.

 

Завдання 533 Барвінок, Котигорошко, Попелюшка та Дюймовочка зліпили 500 вареників. Барвінок зліпив у 2 рази більше вареників, ніж Дюймовочка, Котигорошко — стільки, скільки Барвінок та Дюймовочка разом, а Попелюшка — стільки, скільки Котигорошко та Дюймовочка разом. Скільки вареників зліпила Попелюшка?

Розв'язання

Нехай х (в.) – вареників зліпила Дюймовочка, тоді 2х (в.) – вареників зліпив Барвінок, х + 2х = 3х (в.) – вареників зліпив Котигорошко, х + 3х = 4х (в.) – вареників зліпила Попелюшка. Складемо рівняння

х + 2х + 3х + 4х = 500

10х = 500

х = 500 : 10 

х = 50 (в.) – вареників зліпила Дюймовочка.

2х = 2 • 50 = 100 (в.) – вареників зліпив Барвінок.

3х = 3 • 50 = 150 (в.) – вареників зліпив Котигорошко.

4х = 4 • 50 = 200 (в.) – вареників зліпила Попелюшка.

Відповідь: Дюймовочка зліпила 50 вареників, Барвінок – 100 вареників, Коти горошко – 150 вареників, Попелюшка – 200 вареників.

 

Завдання 534 У трьох вагонах електропоїзда їхало 246 пасажирів. У першому вагоні було у 2 рази більше пасажирів, ніж у другому, а в третьому — на 78 пасажирів більше, ніж у другому. Скільки пасажирів їхало в кожному вагоні?

Розв'язання

Нехай х (п.) – пасажирів у другому вагоні, тоді 2х (п.) – пасажирів у першому вагоні, х + 78 (п.) – пасажирів у третьому вагоні. Складемо рівняння

х + 2х + х + 78 = 246

4х + 78 = 246

4х = 246 – 78

4х = 168

х = 168 : 4

х = (160 + 8) : 4

х = 42 (п.) – пасажирів у другому вагоні.

2х = 2 • 42 = 84 (п.) – пасажирів у першому вагоні.

х + 78 = 42 + 78 = 120 (п.) – пасажирів у третьому вагоні.

Відповідь: у першому вагоні їхало 84 пасажирів, у другому – 42 пасажири, у третьому – 120  пасажирів.

 

Завдання 535 Одна зі сторін трикутника в 5 разів менша від другої і на 25 см менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 74 см.

Розв'язання

Нехай х (см) – перша сторона, тоді 5х (см) – друга сторона, х + 25 (см) – третя сторона. Складемо рівняння

х + 5х + х + 25 = 74

7х + 25 = 74

7х = 74 – 25

7х = 49

х = 49 : 7

х = 7 (см) – перша сторона.

5х = 5 • 7 = 35 (см) – друга сторона.

х + 25 = 7 + 25 = 32 (см) – третя сторона.

Відповідь: перша сторона трикутника дорівнює 7 см, друга сторона – 35 см, третя сторона – 32 см.

 

Завдання 536 На шальках терезів, зображених на рисунку 153, стоять однакові пакети борошна та гирі, маси яких подано в кілограмах. Складіть за цим рисунком рівняння та знайдіть масу одного пакета борошна.

Розв'язання

Нехай х (кг) – маса одного пакета борошна, тоді 3х (кг) – маса трьох таких пакетів. Складемо рівняння.

3х + 6 = 15

3х = 15 – 6

3х = 9

х = 9 : 3

х = 3 (кг) – маса пакета борошна.

Відповідь: маса одного пакета борошна 3 кг.

 

Завдання 537 На шальках терезів, зображених на рисунку 154, стоять однакові пляшки з олією та гирі, маси яких подано в кілограмах. Складіть за цим рисунком рівняння та знайдіть масу однієї пляшки олії.

Розв'язання

Розв'язання

Нехай х (кг) – маса однієї пляшки олії, тоді 4х (кг) – маса чотирьох таких пляшків. Складемо рівняння.

4х + 3 = 11

4х = 11 – 3

4х = 8

х = 8 : 4

х = 2 (кг) – маса пляшки олії.

Відповідь: маса однієї пляшки олії 2 кг.

 

Завдання 538 Поставте в записі 7 • 9 + 12 : 3 – 2 дужки так, щоб значення отриманого виразу дорівнювало: 1) 75; 2) 23.

Розв'язання

(7 • 9 + 12) : (3 – 2) = (63 + 12) : 1 = 75

(7 • 9 + 12) : 3 – 2 = (63 + 12) : 3 – 2 = (21 + 4) – 2 = 25 – 2 = 23 

 

Завдання 539 Поставте в записі 4 • 12 + 18 : 6 + 3 дужки так, щоб значення отриманого виразу дорівнювало: 1) 50; 2) 72.

Розв'язання

4 • 12 + 18 : (6 + 3) = 48 + 2 = 50

4 • (12 + 18 : 6 + 3) = 4 • (12 + 3 + 3) = 4 • 18 = 72 

 

Вправи для повторення

Завдання 540 Периметр чотирикутника ABCD дорівнює 34 см, АВ = 6 см, сторона ВС у 2 рази більша за сторону АВ, сторони CD і AD рівні. Обчисліть довжину сторони AD.

^{Короткий запис}

^{Периметр — 34 см}

^{АВ — 16 см}

^{ВС — ?, у 2 рази більша, ніж АВ}

^{AD — ?, дорівнює СD}

Розв'язання

1) 6 • 2 = 12 (см) – довжина сторони ВС.

2) 6 + 12 = 18 (см) – довжина сторін АВ і ВС разом.

3) 34 – 18 = 16 (см) – довжина сторін CD і AD разом.

4) 16 : 2 = 8 (см) – довжина сторони AD.

Відповідь: довжина сторони AD дорівнює 8 см.

 

Завдання 541 Серед придбаних конвертів 18 виявились рожевого кольору, а 12 конвертів — з марками. Крім того, серед рожевих конвертів 8 було з марками. Скільки всього купили конвертів?

Розв'язання

1) 12 – 8 = 4 (к.) – конвертів іншого кольору.

2) 18 + 4 = 22 (к.) – конвертів всього.

Відповідь: всього купили 22 конверти.

 

Задача від Мудрої Сови

Завдання 527 На столі розташовано 7 зубчастих коліс так, що перше зчеплене з другим, друге — з третім і т. д., а сьоме зчеплене з першим. Чи можуть усі колеса обертатись одночасно? Ні. Щоб колеса оберталися, вони повинні рухатися попарно в протилежні сторони. Це можливо при парній кількості коліс. 

 

------------------------------------------ у підручниках за 2013, 2018 роки ----------------------- 

Завдання 465.* Петрик купив 8 кг печива по 36 грн за кілограм. Скільки кілограмів печива по 24 грн за кілограм він зможе купити за ці самі гроші?

Розв'язання

1 спосіб

1) 36 • 8 = 288 (грн) – вартість печива.

2) 288 : 24 = 12 (кг)

Відповідь: за ці самі гроші можна купити 12 кг печива.

 

Завдання 517.* При яких значеннях а є правильною рівність:

1) 12 : а = 12 а = 12 : 12 а = 1	4) 16 : а = 1  а = 1 • 16 а = 16	7) 16 : а = 0 Нема розв’язку
2) а : 15 = 1  а = 1 • 15 а = 15	5) 1 : а = 1 а = 1 : 1 а = 1	8) а : а = 0 Нема розв’язку
3) а : 1 = 10 а = 10 • 1 а = 10	6) а : 9 = 0 а = 0 • 9 а = 0	9) 0 : а = 5 Нема розв’язку

Завдання 7 Чи існує таке значення a, при якому є правильною рівність:

1) a : 9 = 0 при а = 0

2) 16 : a = 0 не існує значення а.

3) a : a = 0 не існує значення а.

4) 0 : a = 5 не існує значення а

 

Вправа 457°

2) _2668 | 58  232     46   348   348      0

4) _3672 | 34   34       108    27     0    272    272       0

6) _16728 | 68  136      246   312   272    408    408       0

9) _942866 | 178   890        5297    528    356    1726    1602     1246     1246         0

Завдання 458°

2)  _1248 | 24   120      52     48     48      0

3)  _6565 | 13   65       505     6     0     65     65      0

6)  _15652 | 26   156       602      5      0      52      52       0

Завдання 459° 

1) 34 250 000 : 10 = 3 425 000

2) 34 250 000 : 1000 = 34 250

3) 34 250 000 : 10 000 = 3425

4) 25 600 : 80 = 25600 : 10 : 8 = 320

5) 25600 : 800 = 25600 : 100 : 8 = 32

6) 2430000 : 180 = 2430000 : 10 : 3 : 6 = 13500

7) 2430000 : 1800 = 2430000 : 100 : 18 = 1350

8) 243000 : 18000 = 243000 : 1000 : 18 = 135

 

Завдання 460 Виконайте ділення:

1) 32 596 800 : 10 = 3 259 680

2) 876 900 : 100 = 8 769

3) 240 000 : 10 000 = 24

4) 450 000 : 150 = 450 000 : 10 : 15 = 3000

5) 36000 : 12000 = 36000 : 1000 : 12 = 3

6) 124360000 : 40 000 = 124 360 000 : 10 000 : 4 = 3109

 

Завдання 461° Виконайте дії:

1) 256 + 144 : 16 – 8  = 256 + 144 : 2 : 8 – 8 = 257

2) (256 + 144) : (16 – 8) = 400 : 8 = 50

3) (256 + 144) : 16 – 8 = 400 : 16 – 8 = 400 : 8 : 2 – 8 = 17

4) 256 + 144 : (16 – 8) = 256 + 144 : 8 = 256 + 18 = 274

 

Завдання 469

3) 1376 : (621 - 589) + (138 - 69) • 29 = 2044
_621   589   32	_138    69    69	_1376 | 32  128     43     96     96      0	х  69    29   621   138    2001	+2001      43   2044

Завдання 470* 

2) (306 • 307 - 187 • 36) : 45 + 5780 = 7718
х  306     307   2142 918    93942	х  187      36    1122   561     6732	_93942    6732  87210	_87210 | 45    45        1938  422  405   171   135    360    360       0	+1938   5780   7718

Завдання 474* У Петра Івановича є автомобіль ≪Таврія≫. Чи вистачить йому 28 л бензину, щоб доїхати з Києва до Полтави, відстань між якими 337 км, якщо витрата бензину на проїзд 100 км становить 7 л?

^{Короткий запис}

^{100 км – 7 л}

^{х км – 28 л}

Розв'язання

1) 28 : 7 = 4 (разів) – у стільки разів більше бензину.

2) 100 • 4 = 400 (км) – достатня відстань.

Відповідь: так, вистачить бензину.

 

Завдання 481* Відстань між селами Вишневе та Яблуневе дорівнює 15 км. Із цих сіл одночасно в одному напрямі вирушили козаки Чорновус і Сірошапка. Чорновус скакав на коні зі швидкістю 9 км/год і через 3 год після початку руху наздогнав Сірошапку, який ішов пішки. З якою швидкістю йшов Сірошапка?

Розв'язання

1) 9 • 3 = 27 (км) – відстань проскакав козак Чорновус.

2) 27 – 15 = 12 (км) – відстань пройшов козак Сірошапка.

3) 12 : 3 = 4 (км/год) – швидкість козака Сірошапки.

Відповідь: козак Сірошапка йшов із швидкістю 4 км/год.

 

Завдання 482* О 6 год ранку з Мурома до Києва виїхав зі швидкістю 9 км/год Ілля Муромець. О 8 год ранку з Мурома до Києва виїхав Альоша Попович, який наздогнав Іллю Муромця о 2 год дня. З якою швидкістю рухався Альоша Попович?

Розв'язання

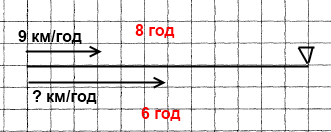
1) 14 - 6 = 8 (год) – час у дорозі Іллі Муромця.

2) 14 - 8 = 6 (год) – час у дорозі Альоші Поповича.

4) 8 • 9 = 72 (км) – відстань.

5) 72 : 6 = 12 (км/год) – швидкість Альоші Поповича.

Відповідь: Альоша Попович рухався зі швидкістю 12 км/год.

 

Завдання 483* О 8 год 57 хв черепаха Катріна вирушила в подорож зі свого ставка до сусіднього. О 9 год 5 хв із цього ж ставка в тому самому напрямі вирушила черепаха Вікторія, як а наздогнала Катріну о 9 год 29 хв. Знайдіть швидкість, з якою рухалася Катріна, якщо відомо, що Вікторія повзла зі швидкістю 8 м/хв.

Розв'язання

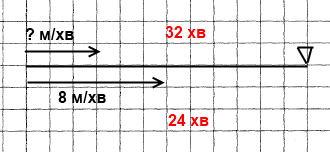
1) 9 год 29 хв – 8 год 57 хв = 32 хв – черепаха Катріна.

2) 9 год 29 хв – 9 год 5 хв = 24 хв – черепаха Вікторія.

3) 8 • 24 = 192 (м) – пройшла черепаха Вікторія

4) 192 : 32 = 6 (км/год) – швидкість черепахи Катріни.

Відповідь: черепаха Катріна рухалась зі швидкістю 6 км/год. 

 

Завдання 488* Буратіно живе на відстані 1 км 200 м від школи. Уроки в школі починаються о 8 год 30 хв. Буратіно робить за хвилину 120 кроків, довжина кроку — 40 см. О котрій годині Буратіно має виходити з дому, щоб приходити до школи за 10 хв до початку занять?

Розв'язання

1) 120 • 40 = 4800 (см) = 48 (м) – відстань за 1 хв.

2) 1200 : 48 = 25 (хв) – час руху до школи.

3) 8 год 30 хв – 10 хв = 8 год 20 хв – час приходу до школи.

4) 8 год 20 хв – 25 хв = 7 год 55 хв

Відповідь: Буратіно має виходити о 7 год 55 хв.   

 

Завдання 486* Школярі Василько, Андрійко, Данилко і Сергійко зібрали 326 кг моркви. Василько зібрав 37 кг моркви, що в 3 рази менше, ніж Андрійко, а Данилко і Сергійко зібрали моркви порівну. Хто зі школярів зібрав більше моркви?

Розв'язання

1) 37 • 3 = 111 (кг) – зібрав Андрійко.

2) 37 + 111 = 148 (кг) – зібрали Василько і Андрійко разом.

3) (326 – 148) : 2  = 89 (кг) – зібрали окремо Данилко і Сергійко.

Відповідь: найбільше моркви зібрав Андрійко.

 

Завдання 487* Робітники Іван, Петро, Степан і Павло виготовили 160 деталей. Іван виготовив 81 деталь, що у 3 рази більше, ніж Петро, а Степан і Павло виготовили деталей порівну. Хто з робітників виготовив найменше деталей?

Розв'язання

1) 81 : 3 = 27 (д.) – виготовив Петро.

2) 81 + 27 = 108 (д.) – виготовили Іван і Петро разом.

3) (160 – 108) : 2 = 26 (д.) – виготовили окремо Степан і Павло.

Відповідь: найменше деталей виготовив Степан та Павло.

 

Завдання 493 Білочки Руденька та Жовтенька збирали горіхи. Руденька зібрала 6 мішечків горіхів, а Жовтенька — 7 таких самих мішечків. Разом вони зібрали 52 кг горіхів. Скільки кілограмів горіхів зібрала Руденька і скільки — Жовтенька?

Розв'язання

1) 6 + 7 = 13 (м) – мішечків горіхів зібрали білочки.

2) 52 : 13 = 4 (кг) – горіхів у 1 мішечку.

3) 4 • 6 = 24 (кг) – горіхів зібрала Руденька.

4) 4 • 7 = 28 (кг) – горіхів зібрала Жовтенька.

Відповідь: Руденька зібрала 24 кг горіхів, Руденька – 28 кг горіхів.

 

Завдання 494* Рухаючись пустелею протягом 3 днів, караван подолав 63 км. Першого дня караван рухався 6 год, другого — 8 год, а третього — 7 год. Скільки кілометрів проходив караван кожного дня, якщо відомо, що він рухався всі дні зі сталою швидкістю?

Розв'язання

1) 6 + 8 + 7 = 21 (год) – час руху каравану.

2) 63 : 21 = 3 (км/год) – швидкість каравану.

3) 3 • 6 = 18 (км) – відстань за перший день. 

4) 3 • 8 = 24 (км) – відстань за другий день.

5) 3 • 7 = 21 (км) – відстань за третій день.

Відповідь: першого дня караван пройшов 18 км, другого - 24 км, третього - 21 км.

 

Завдання 512 Червона Шапочка, Мальвіна, Попелюшка та Дюймовочка зліпили 500 вареників. Червона Шапочка зліпила у 2 рази більше вареників, ніж Дюймовочка, Мальвіна — стільки, скільки Червона Шапочка та Дюймовочка разом, а Попелюшка — стільки, скільки Мальвіна та Дюймовочка разом. Скільки вареників зліпила кожна дівчинка?

Розв'язання

Нехай х (в.) – вареників зліпила Дюймовочка, тоді 2х (в.) – вареників зліпила Червона Шапочка, х + 2х = 3х (в.) – вареників зліпила Мальвіна, х + 3х = 4х (в.) – вареників зліпила Попелюшка. Складемо рівняння

х + 2х + 3х + 4х = 500

10х = 500

х = 500 : 10 

х = 50 (в.) – вареників зліпила Дюймовочка.

2х = 2 • 50 = 100 (в.) – вареників зліпила Червона Шапочка.

3х = 3 • 50 = 150 (в.) – вареників зліпила Мальвіна.

4х = 4 • 50 = 200 (в.) – вареників зліпила Попелюшка.

Відповідь: Дюймовочка зліпила 50 вареників, Червона Шапочка – 100 вареників, Мальвіна – 150 вареників, Попелюшка – 200 вареників. 

 

Завдання 514 Між трьома школами розподілили 552 кг апельсинів, причому одна школа отримала в 6 разів менше апельсинів, ніж друга, і на 136 кг менше, ніж третя. Скільки кілограмів апельсинів отримала кожна школа?

Розв'язання

Нехай х (кг) – апельсинів отримала перша школа, тоді 6х (кг) – апельсинів отримала друга школа, х + 136 (кг) – апельсинів отримала третя школа. Складемо рівняння

х + 6х + х + 136 = 552

8х = 552 – 136

8х = 416

х =  416 : 8

х = (400 + 16) : 8

х = 52 (кг) – апельсинів отримала перша школа.

6х = 6 • 52 = 312 (кг) – апельсинів отримала друга школа.

х + 136 = 52 + 136 = 188 (кг) – апельсинів отримала третя школа.

Відповідь: перша школа отримала 52 кг апельсини, друга школа – 312 кг апельсинів, третя школа – 188 кг апельсинів.

 

Завдання 516 Одна зі сторін трикутника у 2 рази більша за другу сторону, а друга — на 7 дм менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 99 дм.

Розв'язання

Нехай х (дм) – друга сторона, тоді 2х (дм) – перша сторона, х + 7 (дм) – третя сторона. Складемо рівняння

х + 2х + х + 7 = 99

4х + 7 = 99

4х = 99 – 7

4х = 92

х = 92 : 4

х = (80 + 12) : 4

х = 23 (дм) – друга сторона.

2х = 2 • 23 = 46 (дм) – перша сторона.

х + 7 = 23 + 7 = 30 (дм) – третя сторона.

Відповідь: довжина першої сторони 46 дм, другої – 23 дм, третьої – 30 дм.

 

Завдання 517

1) Чи правильно, що коли кожний доданок ділиться на деяке число, то й сума цих доданків ділиться на це число? Проілюструйте свою відповідь прикладами.

Розв'язання

Правильно.

10 : 2 + 12 : 2 = 5 + 6 = 11

(10 + 12) : 2 = 22 : 2 = 11

2) Чи може сума кількох доданків ділитися на деяке число, якщо кожний доданок не ділиться на це число? Проілюструйте свою відповідь прикладами.

Розв'язання

Так, може.

(10 + 25 + 1) : 3 = 36 : 3 = 12

Сума ділиться на 3, а кожен доданок не ділиться на 3. 

 

Завдання 518 Як зміниться частка, якщо:

1) ділене збільшити в 7 разів; 2) ділене зменшити у 2 рази; 3) дільник збільшити в 4 рази; 4) дільник зменшити в 5 разів; 5) ділене збільшити у 8 разів, а дільник — у 2 рази; 6 ) ділене зменшити в 9 разів, а дільник — у 3 рази; 7) ділене збільшити в 6 разів, а дільник зменшити у 2 рази; 8) ділене зменшити в 6 разів, а дільник збільшити у 2 рази?

Розв'язання

1) Збільшиться в 7 разів

2) зменшиться в 2 рази

3) зменшиться в 4 рази

4) збільшиться в 5 разів

5) збільшиться в 4 рази (частка збільшиться у 8 разів, потім частка зменшиться у 2 рази,

маємо 8 : 2 = 4)

6) зменшиться в 3 рази (частка зменшиться в 9 разів, частка збільшиться в 3 рази,

9 : 3 = 3)

7) збільшиться в 12 разів (частка збільшиться в 6 разів, частка збільшиться у 2 рази,

6 • 2 = 12)  

8) зменшиться в 12 разів (частка зменшиться в 6 разів, частка зменшиться у 2 рази,

6 • 2 = 12)

 

Завдання 519 Ділене збільшили в 3 рази. Як треба  змінити дільник, щоб частка: 1 ) збільшилась у 6 разів; 2) зменшилась у 6 разів; 3) не змінилася?

Розв'язання

1) Дільник зменшити у 2 рази (частка збільшилась в 3 рази, частку збільшити у 2 рази)

2) Дільник збільшити у 18 разів (частка збільшилась у 3 рази, частку зменшити у 18 разів)

3) Дільник збільшити у 3 рази (частка збільшилась в 3 рази, частку зменшити у 3 рази)

 

Завдання 520* Обчисліть зручним способом:

1) (44 • 58) : 11 = 44 : 11 • 58 = 4 • 58 = (50 + 8) • 4 = 232 

2) (69 • 60) : 30 = 60 : 30 • 69 = 69 • 2 = (60 + 9) • 2 = 138  

3) (63 • 88) : 21 = 63 : 21 • 88 = 3 • 88 = (80 + 8) • 3 = 240 + 24 = 264 

4) (350 • 48) : 70 = 350 : 70 • 48 = 5 • 48 = (40 + 8) • 5 = 240 

5) (2 • 17 • 14) : 28 = (17 • 2 • 14) : 28 = (17 • 28 ) : 28 = 28 : 28 • 17 = 17 

6) (21 • 18) : 14 = (21 • 18) : (7 • 2) = 21 : 7 • 18 : 2 = 3 • 9 = 27

 

Завдання 521** Обчисліть зручним способом:

1) (36 • 21) : 12 = 36 : 12 • 21 = 3 • 21 = 63

2) (40 • 420) : 60 = 420 : 60 • 40 = 7 • 40 = 280

3) (5 • 6 • 78) : 3 = 6 : 3 • 5 • 78 = 10 • 78 = 780

4) (45 • 63) : 81 = (45 • 63) : (9 • 9) = 45 : 9 • 63 : 9 = 5 • 7 = 35

 

Завдання 524* Складіть числовий вираз із використанням тільки знаків чотирьох арифметичних дій та чотирьох цифр 2 так, щоб значення отриманого виразу дорівнювало: 1) 1; 2) 2; 3)3; 4) 4; 5) 5; 6) 6; 7) 8; 8) 10.

Розв'язання

1) 2 : 2 + 2 – 2 = 1

2) 2 : 2 + 2 : 2 = 2

3) 2 + 2 – 2 : 2 = 3

4) 2 • 2 • 2 : 2 = 4

5) 2 + 2 + 2 : 2 = 5

6) 2 • 2 • 2 – 2 = 6

7) 2 • 2 + 2 • 2 = 8

8) (22 – 2) : 2 = 10  або 2 • 2 • 2 + 2= 10

 Інші завдання дивись тут ...