Коло, вписане у трикутник, — це коло, яке дотикається до всіх сторін цього трикутника.
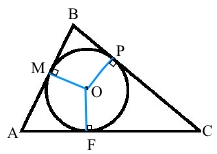
Коло з центром O – вписане коло у трикутник АВС.
Точки M, N, P – точки дотику кола до сторін трикутника (OM ﬩ АВ, OP ﬩ ВС, OF ﬩ АС).
Зауважимо, що при цьому трикутник називають описаним навколо кола.
∆ABC – трикутник, описаний навколо кола.
◊ Теорема (про коло, вписане у трикутник).
У будь-який трикутник можна вписати коло.
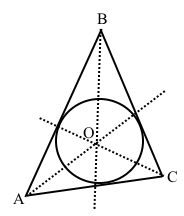
Наслідок. Бісектриси трикутника перетинаються в одній точці.
Наслідок. Центр кола, вписаного у трикутник, – точка перетину бісектрис цього трикутника (інцентр).
Центр кола, вписаного у трикутник
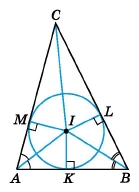
• Центр кола, вписаного у трикутник, — це точка перетину бісектрис трикутника.
І – центр вписаного кола у трикутник, точка перетину АІ – бісектриса кута А (∠ІАС = ∠ІАВ), СІ – бісектриса кута С (∠ІСА = ∠ІСВ), ВІ – бісектриса кута В (∠ІВС = ∠ІВА).
• Центр вписаного кола у трикутник рівновіддалений від сторін трикутника.
Точки I, L, K – точки дотику вписаного кола до сторін трикутника. Відрізки МІ ﬩ АС, LI ﬩ ВС, КІ ﬩ АВ, причому МІ = LI = KI = r, де r – радіус вписаного кола.
Висновок
Нехай коло з центром О, вписане у трикутник.
1) Через центр кола О і кожну з вершин трикутника можна провести бісектрису трикутника (за теоремою і наслідками).
2) Точка дотику кола до відповідної сторони трикутника лежить на радіусі, який перпендикулярний до цієї сторони (за означенням вписаного кола у трикутник).
3) Центр кола, вписаного у трикутник, рівновіддалений від сторін трикутника (за властивістю бісектриса кута).