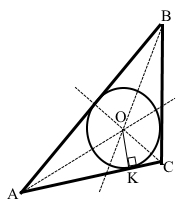
◊ Теорема (про коло, вписане у трикутник).
У будь-який трикутник можна вписати коло.
Наслідок. Бісектриси трикутника перетинаються в одній точці.
Наслідок. Центр кола, вписаного у трикутник, – точка перетину бісектрис цього трикутника (інцентр).
1) Креслимо трикутник будь-якого виду.
Трикутник АМN – гострокутний.
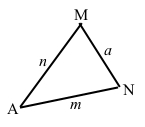
2) За допомогою транспортира і лінійки проводимо бісектрису для першого кута А трикутника.
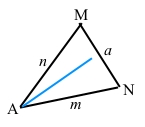
3) За допомогою транспортира і лінійки проводимо бісектрису для другого кута M трикутника.
Нас цікавить точка перетину трьох бісектрис трикутника. Зазвичай, якщо впевнені, що правильно поділили два кути і дві бісектриси проведені правильно, тоді крок 4 можна пропустити.
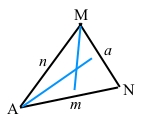
4) За допомогою транспортира і лінійки проводимо бісектрису для третього кута N трикутника.
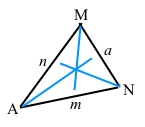
Якщо три бісектриси перетнулися в одній точці, тоді нема сумніву щодо правильності побудови бісектрис трикутника.
5) Точка перетину бісектрис О буде центром кола, вписаного у трикутник.
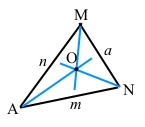
6) З точки О за допомогою лінійки і транспортира (простіше за допомогою косинця) проводимо перпендикуляр до одної із сторін трикутника, наприклад, АN.
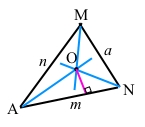
7) Позначимо точку перетину перпендикуляра зі стороною AN точкою К. Ця точка буде точкою дотику кола до сторони АN трикутника (за означенням вписане коло дотикається до сторін трикутника).
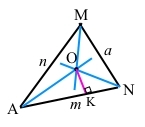
8) За допомогою циркуля будуємо коло з центром у точці О радіусом AK.
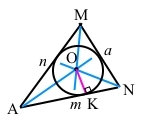
Висновок
Коло з центром О вписане у трикутник AMN, тоді трикутник AMN описаний навколо кола з центром О.
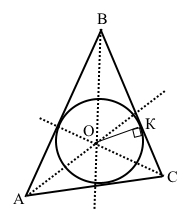
Приклади вписаних кіл у трикутники різних видів
Коло з центром у точці О радіусом ОК вписане у гострокутний трикутник АВС:
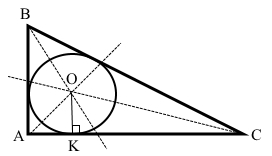
Коло з центром у точці О радіусом ОК вписане у прямокутний трикутник АВС:
Коло з центром у точці О радіусом ОК вписане у тупокутний трикутник АВС: