Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 9 Кути, утворені при перетині двох прямих січною, ознаки паралельності прямих
Завдання 182
Кути 1 і 2 на малюнках 9.7-9.9: внутрішні різносторонні кути, відповідні кути, внутрішні односторонні кути.
Завдання 183
Кути 1 і 2 на малюнках 9.10-9.12: внутрішні односторонні кути, відповідні кути, внутрішні різносторонні кути.
Завдання 184 Малюнок 9.13.
Усі пари внутрішніх односторонніх кутів: ANL і BMK, CNL і KMD.
Усі пари внутрішніх різносторонніх кутів: ANL і KMD, CNL і BMK.
Усі пари відповідних кутів: ANK і BMK, ANL і BML, KNC і KND, LNC і LMD.
Завдання 185 Малюнок 9.14.
Усі пари внутрішніх односторонніх кутів: PCK і DMB, KCF і BML.
Усі пари внутрішніх різносторонніх кутів: PCK і BML, KCF і BMD.
Усі пари відповідних кутів: PCB і DMB, PCK і DMK, BCF і BML, KCF і KML.
Завдання 186 Малюнок 19.5
Прямі AB і CD паралельні, оскільки згідно наслідку 3 є перпендикулярними до одної прямої АС.
Завдання 187 Ознаки паралельності прямих
На малюнку 9.16 прямі a і b є паралельними, бо позначені відповідні кути рівні (згідно теореми – ознаки паралельності прямих).
На малюнку 9.17 прямі a і b перетинаються, бо сума внутрішніх односторонніх кутів не дорівнює 180°, а саме 45° + 130° ∠ 180° (суперечить наслідку 2).
На малюнку 9.18 прямі a і b є паралельними, бо позначені відповідні кути рівні (згідно теореми – ознаки паралельності прямих).
На малюнку 9.19 прямі a і b перетинаються, бо позначені відповідні кути нерівні, а саме 119° ≠ 120° (суперечить теоремі – ознаці паралельності прямих).
На малюнку 9.20 прямі a і b паралельні, бо сума внутрішніх односторонніх кутів дорівнює 180°, а саме 100° + 80° = 180° (згідно наслідку 2).
На малюнку 9.21 прямі a і b перетинаються, бо позначені відповідні кути нерівні, а саме 110° ≠ 98° (суперечить теоремі – ознаці паралельності прямих).
Завдання 188
На малюнку 9.22 позначено міри двох кутів, що утворилися при перетині прямих m і n січною p. Обчисліть міри всіх інших кутів, що утворилися. Чи паралельні прямі m і n?
Розглянемо прямі m і p, що перетинаються. Вони утворюють дві пари вертикальних кутів, також дві пари суміжних кутів, тому 180° – 70° = 110° – суміжний кут з поданим. Він буде відповідним до поданого кута 120° при перетині прямих m і n січною p. Оскільки відповідні кути не є рівними, тому прямі m і n не є паралельними.
Розглянемо прямі n і p, що перетинаються. Вони утворюють дві пари вертикальних кутів, також дві пари суміжних кутів, тому 180° – 120° = 60° – суміжний кут з поданим. Отже, для прямих m і n та січної р маємо такі кути:
внутрішні односторонні кути: 70° і 120°, 110° і 60°;
внутрішні різносторонні кути: 70° і 60°, 120° і 110°;
відповідні кути по дві пари: 70° і 60°, 110° і 120°.
Завдання 189
На малюнку 9.23 позначено міри двох кутів, що утворилися при перетині прямих a і b січною d. Обчисліть міри всіх інших кутів, що утворилися. Чи паралельні прямі a і b?
Розглянемо прямі a і d, що перетинаються. Вони утворюють дві пари вертикальних кутів, також дві пари суміжних кутів, тому 180° – 50° = 130° – суміжний кут з поданим. Він буде відповідним до поданого кута 130° при перетині прямих a і b січною d. Оскільки відповідні кути є рівними, тому прямі a і b є паралельними.
Розглянемо прямі b і d, що перетинаються. Вони утворюють дві пари вертикальних кутів, також дві пари суміжних кутів, тому 180° – 130° = 50° – суміжний кут з поданим. Отже, для прямих a і b та січної d маємо такі кути:
дві пари внутрішніх односторонніх кутів: 50° і 130°;
внутрішні різносторонні кути: 130° і 130°, 50° і 50°;
відповідні кути по дві пари: 130° і 130°, 50° і 50°.
Завдання 190
Доповнили малюнок 9.24: провели пряму CM так, щоб кути ABC і BCM були внутрішніми різносторонніми кутами для прямих AB і CM та січної BC.
Точки A і M розмістяться по різні сторони відносно прямої BC.
Завдання 191
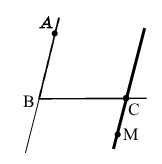
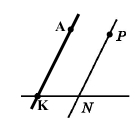
Доповнили малюнок 9.25: провели пряму KA так, щоб кути AKN і KNP були внутрішніми односторонніми кутами для прямих AK і PN та січної KN.
Точки A і P розмістяться по одну сторону відносно прямої KN.
Завдання 192
На малюнку 9.26 укажіть паралельні прямі, якщо ∠1 = 118°, ∠2 = 62°, ∠3 = 63°.
Розглянемо прямі b і c та січну m. Оскільки відповідні кути ∠2 ≠ ∠3, то прямі b і c не є паралельними.
Розглянемо прямі a і m, що перетинаються. Вони утворюють дві пари вертикальних кутів, також дві пари суміжних кутів, тому 180° – ∠1 = 180° – 118° = 62° – другий суміжний кут. Він дорівнює відповідному куту ∠2 для прямих a і b та січної m.
Отже, прямі a і b є паралельними.
Завдання 193
На малюнку 9.26 укажіть паралельні прямі, якщо ∠1 = 121°, ∠2 = 60°, ∠3 = 60°.
Розглянемо прямі b і c та січну m. Оскільки відповідні кути ∠2 = ∠3, то прямі b і c є паралельними.
Розглянемо прямі a і m, що перетинаються. Вони утворюють дві пари вертикальних кутів, також дві пари суміжних кутів, тому 180° – ∠1 = 180° – 121° = 59° – другий суміжний кут. Він не дорівнює відповідному куту ∠2 для прямих a і b та січної m, тому прямі a і b не є паралельними.
Отже, прямі b і c є паралельними.
Завдання 194 Малюнок 9.27.
Через точку A за допомогою двох креслярських косинців провели пряму a таким чином, що уявна січна, яка розміщена вертикально, є перпендикулярною до прямої а і прямої b. Позначимо уявну січну буквою с. Маємо а ⊥ с і b ⊥ c, тоді із третього наслідку випливає, що прямі a і b є паралельними (а || b).
Завдання 195 Малюнок 9.28.
1) Виміряли ∠ABC = 110°.
2) Побудували ∠PCK, що дорівнює куту ABC і є йому відповідним.
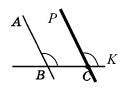
3) Утворилися паралельні прямі АВ і РС, оскільки відповідні кути рівні ∠АВС = ∠PCK.
Завдання 196
1) Виміряли ∠MNP = 120°.
2) Побудували ∠APB, що дорівнює куту MNP і є йому відповідним.
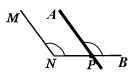
3) Утворилися паралельні прямі MN і AP, оскільки відповідні кути рівні ∠MNP = ∠APB.
Завдання 197
Пряма AB перетинає пряму CD у точці A, а пряму MN – у точці B, ∠CAB = 90°, ∠ABN = 90°. Чи паралельні прямі CD і MN?
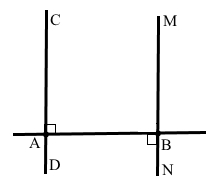
Якщо один з чотирьох кутів, що утворилися при перетині двох прямих, прямий, тоді всі інші також прямі.
Тому маємо суму внутрішніх односторонніх кутів ∠CAB + ∠MBA = 90° + 90° = 180°.
Отже згідно наслідку 2 можна стверджувати, що CD || MN.
Завдання 198
На малюнку 9.30 ∠1 + ∠2 = 180°. Доведіть, що a || b.
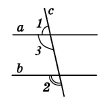
Дано січна с до прямих а і b, ∠1 + ∠2 = 180°.
Нехай ∠1 + ∠2 = 180°, тоді ∠1 = 180° – ∠2.
Прямі а і с перетинаються, тоді маємо дві пари суміжних кутів, наприклад, ∠3 = 180° – ∠1,
∠3 = 180° – (180° – ∠2) = 180° – 180° + ∠2 = ∠2.
Кути 3 і 2 є відповідними для прямих a і b та січної c.
Відповідні кути рівні, отже прямі a і b паралельні (a || b).
Завдання 199
На малюнку 9.31 ∠1 = ∠2. Доведіть, що прямі m || n.
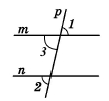
Дано січна p до прямих m і n, ∠1 = ∠2.
Нехай прямі m і p перетинаються, тоді маємо дві пари вертикальних кутів, наприклад,
∠1 = ∠3. Кути ∠3 і ∠2 є відповідними для прямих m і n та січної p. Відповідні кути рівні, отже прямі m і n паралельні (m || n)
Завдання 200 Малюнок 9.32.
1) ∠4 + ∠5 = 190°. Знайдіть ∠2 + ∠7.
Пряма а, що перетинається зі січною, утворює пару вертикальних кутів ∠4 = ∠2.
Пряма b, що перетинається із січною, утворює пару вертикальних кутів ∠5 = ∠7.
∠2 + ∠7 = ∠4 + ∠5 = 190°.
2) ∠4 + ∠5 = 190°. Знайдіть ∠1 + ∠8.
Пряма а, що перетинається зі січною, утворює пару суміжних кутів ∠1 + ∠4 = 180°.
Пряма b, що перетинається із січною, утворює пару суміжних кутів ∠5 + ∠8 = 180°.
∠1 + ∠8 = (180° – ∠4) + (180° – ∠5) = 180° + 180° – ∠4 – ∠5 = 360° – (∠4 + ∠5) = 360° – 190° = 170°.
3) ∠4 + ∠5 = 190°. Знайдіть ∠3 + ∠6.
Пряма а, що перетинається зі січною, утворює пару суміжних кутів ∠4 + ∠3 = 180°.
Пряма b, що перетинається із січною, утворює пару суміжних кутів ∠5 + ∠6 = 180°.
∠3 + ∠6 = (180° – ∠4) + (180° – ∠5) = 180° + 180° – ∠4 – ∠5 = 360° – (∠4 + ∠5) = 360° – 190° = 170°.
Завдання 201 Малюнок 9.32.
1) ∠3 + ∠6 = 160°. Знайдіть ∠2 + ∠7.
Пряма а, що перетинається зі січною, утворює пару суміжних кутів ∠2 + ∠3 = 180°.
Пряма b, що перетинається із січною, утворює пару суміжних кутів ∠6 + ∠7 = 180°.
∠2 + ∠7 = (180° – ∠3) + (180° – ∠6) = 180° + 180° – ∠3 – ∠6 = 360° – (∠3 + ∠6) = 360° – 160° = 200°.
2) ∠3 + ∠6 = 160°. Знайдіть ∠1 + ∠8.
Пряма а, що перетинається зі січною, утворює пару вертикальних кутів ∠3 = ∠1.
Пряма b, що перетинається із січною, утворює пару вертикальних кутів ∠6 = ∠8.
∠1 + ∠8 = ∠3 + ∠6 = 160°.
3) ∠3 + ∠6 = 160°. Знайдіть ∠4 + ∠5.
Пряма а, що перетинається зі січною, утворює пару суміжних кутів ∠4 + ∠3 = 180°.
Пряма b, що перетинається із січною, утворює пару суміжних кутів ∠5 + ∠6 = 180°.
∠4 + ∠5 = (180° – ∠3) + (180° – ∠6) = 180° + 180° – ∠3 – ∠6 = 360° – (∠3 + ∠6) = 360° – 160° = 200°.
Завдання 202
∠ABC = 70°, ∠BCD = 100°. Чи можуть прямі AB і CD бути паралельними? Відповідь обґрунтуйте.
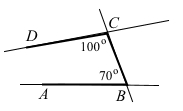
Кути ∠ABC = 70° і ∠BCD = 100° можна розглядати як внутрішні односторонні кути прямих АВ і СD та січної BC. Знайдемо їхню суму ∠ABC + ∠BCD = 100° + 70° = 170°, сума внутрішніх односторонніх кутів не дорівнює 180°. Отже, прямі AB і CD не можуть бути паралельними.
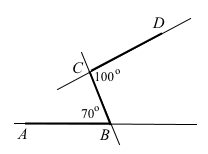
Кут ∠BCD = 100° можна розглядати як вертикальний кут при перетині двох прямих АВ і С, який буде відповідним до кута АВС для прямих АВ і СD та січної BC. Ці відповідні кути не є рівними. Отже, прямі AB і CD не можуть бути паралельними.
Відповідь: ні.
Завдання 203
∠MNP = 60°, ∠NPK = 120°. Чи можуть прямі MN і KP бути паралельними? Відповідь обґрунтуйте.
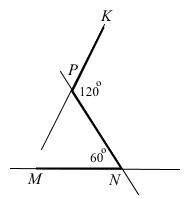
Кут ∠NPK = 120° можна розглядати як вертикальний кут при перетині двох прямих і , який є відповідним до кута ∠MNP = 60°. Ці відповідні кути не є рівними, отже при такому розміщенні прямі не є паралельними.
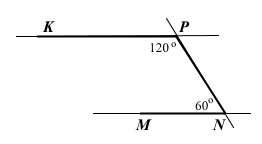
Кути ∠MNP = 60° і ∠NPK = 120° можна розглядати як внутрішні односторонні кути прямих MN і KP та січної NP. Знайдемо їхню суму ∠MNP + ∠NPK = 60° + 120° = 180°, сума внутрішніх односторонніх кутів дорівнює 180°. Отже, прямі MN і KP можуть бути паралельними.
Відповідь: так.
Завдання 204
Кут між прямими a і b дорівнює куту між прямими b і c. Чи можна стверджувати, що прямі a і c паралельні?
Якщо утворився кут між прямими a і b, тоді вони перетинаються. Якщо утворився кут між прямими b і c, тоді вони перетинаються. Можна стверджувати, що пряма b перетинає прямі a і c. Якщо прямі a і b розмістити так, що кути між прямими a і b, b і c будуть рівними відповідними кутами для прямих а і с та січної b, тоді можна стверджувати, що прямі a і c паралельні.
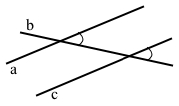
Інакше прямі а і с не будуть паралельними.
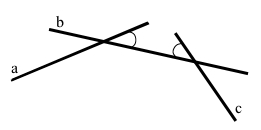
Відповідь: ні.
Завдання 205
Пряма c є січною для прямих a і b. Чотири з восьми кутів, що утворилися, дорівнюють по 30°, а решта чотири – по 150°. Чи можна стверджувати, що прямі a і b паралельні?
Пряма a із січною с утворює дві пари вертикальних кутів по 30° і по 150° , дві пари суміжних кутів 30° + 150° = 180°.
Пряма b із січною с утворює дві пари вертикальних кутів по 30° і по 150° , дві пари суміжних кутів 30° + 150° = 180°. Якщо прямі a і b розмістити так, що кути між прямими a і c, b і c будуть рівними відповідними кутами для прямих а і b та січної с, тоді можна стверджувати, що прямі a і b паралельні.
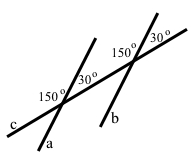
Інакше прямі а і b не будуть паралельними.
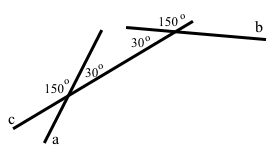
Відповідь: ні.
Завдання 206 Малюнок 9.33.
MF – бісектриса кута KMN, KF – бісектриса кута MKP. ∠MKF + ∠FMK = 90°. Доведіть, що MN || KP.
Нехай ∠MKF + ∠FMK = 90°. MF – бісектриса кута KMN, тоді ∠KMN = 2∠FMK, KF – бісектриса кута MKP, тоді ∠MKP = 2∠MKF.
Знайдемо суму внутрішніх односторонніх кутів ∠KMN + ∠MKP = 2∠FMK + 2∠MKF = 2 • (∠FMK + ∠MKF) = 2 • 90° = 180°. Отже, прямі паралельні MN || KP.
Завдання 207
Прямі a і b перпендикулярні до прямої m. Пряма c перетинає пряму a. Чи перетинаються прямі b і c? Відповідь обґрунтуйте.
Дано а ⊥ m і b ⊥ m. Згідно наслідку 3 дві прямі a і b перпендикулярні до третьої прямої m є паралельними а || b.
Згідно теореми, коли січна с перетинає одну з двох паралельних прямих а, тоді вона перетинає другу паралельну їй пряму b. Отже, прямі b і с перетинаються.
Вправи для повторення
Завдання 208
1) Накреслили ∠ABC = 70° і позначили точку K, що належить променю BA.
2) Через точку K за допомогою косинця провели пряму m, перпендикулярну до променя BA, та пряму n, перпендикулярну до променя BC.
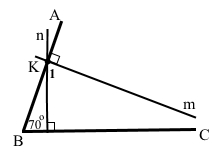
3) Користуючись транспортиром, знайшли кут між прямими m і n ∠1 = 70°.
Завдання 209
Відомо, що ∠AOB = ∠BOC = 130°. Знайдіть ∠AOC.
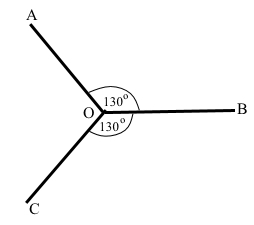
Точка О є спільною вершиною кутів AOB і BOC, точка В належить спільній стороні. Якщо промінь ОВ проходить між сторонами кута, тоді ∠АОВ + ∠ВОС = 130° + 130° = 260°, звідси ∠АОС = 360° – 260° = 100°.
Відповідь: ∠AOC = 100°.
Життєва математика
Завдання 210 Задача-жарт. Зріст Сергія 1 м 60 см (1,6 м). На скільки кілометрів верхівка голови Сергія пройшла б більше, ніж кінець його ноги, якби він мав змогу пройти земну кулю по її екватору?
Нехай – радіус Землі від її центру до екватора, тоді довжина екватора l1 = 2πR.
Уявимо, що людинa переміщується тілом перпендикулярно до екватора, тоді на рівні її ніг маємо радіус R, а на рівні голови буде радіус R + h, де h – це зріст людини.
Тоді довжина такого кола l1 = 2π(R + h).
Щоб порівняти довжини кіл, треба знайти різницю між більшою і меншою довжиною, тому l1 – l2 = 2π(R + h) – 2πR = 2π(R + h – R) = 2πh = 2 • 3,14 • 1,6 ≈ 10,048 (м)
10,048 м = (10,048 : 1000) км ≈ 0, 010048 км
Відповідь: приблизно на 0,010048 км більше.
Завдання 211 Чи можна трикутник розрізати на частини так, щоб утворилося три чотирикутники? Якщо так, то виконайте це.