Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 12 Рівність геометричних фігур
Завдання 301
1) Виміряйте довжини відрізків AB і CD на малюнку 12.3 та встановіть, чи рівні вони.
АВ = 25 мм
CD = 28 мм
Відрізки АВ і CD не є рівні.
2) Виміряйте кути M і K на малюнку 12.4 та встановіть, чи рівні вони.
∠М = 50°.
∠К = 50°.
∠М = ∠К Кути М і К рівні.
Завдання 302
1) Виміряйте довжини відрізків MN і PK на малюнку 12.5 та встановіть, чи рівні вони.
MN = 3 см
PK = 3 см
MN = PK Відрізки MN і PK рівні.
2) Виміряйте кути A і B на малюнку 12.6 та встановіть, чи рівні вони.
∠A = 60°.
∠B = 50°.
Кути A і В не є рівні.
Завдання 303
1) Чи можна сумістити накладанням відрізки AK і MF, якщо AK = 1,7 см, а MF = 17 мм?
Оскільки 1,7 см = 17 см, то довжини відрізків рівні, значить відрізки рівні АК = MF.
Рівні відрізки можна сумістити накладанням.
2) Чи можна сумістити накладанням кути, градусні міри яких дорівнюють 27° і 31°?
Оскільки градусні міри кутів різні, значить кути не є рівні.
Нерівні кути не можна сумістити накладанням.
Завдання 304
Дано: ∆ABC = ∆MPL. Доповніть записи (у рівних трикутників відповідні кути рівні).
1) ∠A = ∠М ; 2) ∠AB = ∠М ; 3) ∠C = ∠L.
Завдання 305
Дано: ∆MPT = ∆DCK. Доповніть записи (у рівних трикутників відповідні сторони рівні):
1) MP = DC; 2) PT = CK; 3) MT = DK.
Завдання 306
На малюнку 12.7 зображено рівні трикутники. Доповніть записи рівності трикутників:
1) ∆AKM = ∆LPT; 2) ∆MAK = ∆TLP.
Завдання 307
На малюнку 12.8 зображено рівні трикутники. Доповніть записи рівності трикутників:
1) ∆ABC = ∆PFK ; 2) ∆CAB = ∆KPF.
Завдання 308
Відомо, що ∆ABC = ∆KLP, AB = 6 см, LP = 8 см, AC = 10 см. Знайдіть невідомі сторони трикутників ABC і KLP.
У рівних трикутників відповідні сторони рівні.
KL = AB = 6 см
KP = AC = 10 см
BC = LP = 8 см
Завдання 309
Відомо, що ∆PMT = ∆DCF, ∠P = 41°, ∠C = 92°, ∠T = 47°. Знайдіть невідомі кути трикутників PMT і DCF.
У рівних трикутників відповідні кути сторони рівні.
∠D = ∠P = 41°
∠M = ∠C = 92°
∠F = ∠T = 47°
Завдання 310
1) Периметри двох трикутників рівні. Чи можна стверджувати, що ці трикутники рівні?
Ні. Трикутники рівні, якщо вони накладаються при суміщенні. Трикутники з однаковими периметрами можуть не накладатися при суміщенні.
2) Периметр одного трикутника більший за периметр другого. Чи можуть ці трикутники бути рівними?
Ні. Якщо трикутники накладаються при суміщенні, тоді вони рівні. У рівних трикутників однаковий периметр.
Завдання 311
Відомо, що ∆ABC = ∆CBA. Чи є у трикутника ABC рівні сторони? Якщо так, назвіть їх.
У рівних трикутників відповідні сторони рівні.
Запишемо рівності для відповідних сторін: АВ = СВ, ВС = ВА, АС = СА.
Оскільки друга рівність повторює першу, а третя рівність стосується того самого відрізка, тоді маємо дві рівні сторони АВ = ВС.
Відповідь: у трикутника ABC рівні дві сторони АВ = ВС.
Завдання 312
Відомо, що ∆MNK = ∆MKN. Чи є у трикутника MNK рівні кути? Якщо так, назвіть їх.
У рівних трикутників відповідні кути рівні.
Запишемо рівності для відповідних кутів : ∠M = ∠M, ∠N = ∠K, ∠K = ∠N.
Оскільки друга рівність повторює третю, а перша рівність стосується того самого кута, тоді маємо два рівні кути ∠N = ∠K.
Відповідь: у трикутника MNK рівні два кути ∠N = ∠K .
Завдання 313
Дано: ∆ABC = ∆BCA. Знайдіть периметр трикутника ABC, якщо AB = 7 см.
У рівних трикутників відповідні сторони рівні.
Запишемо рівності для відповідних сторін: АВ = ВС, ВС = СА, СА = АВ.
АВ = 7 см.
ВС = АВ = 7 см.
СА = ВС = 7 см.
Маємо рівносторонній трикутник.
Р = 7 • 3 = 21 (см)
Відповідь: 21 см.
Завдання 314
Дано: ∆PKL = ∆KLP. Знайдіть PK, якщо периметр трикутника PKL дорівнює 27 см.
У рівних трикутників відповідні сторони рівні.
Запишемо рівності для відповідних сторін: PK = KL, KL = LP, PL = KP (LP = PK).
PK = KL = LP
Маємо рівносторонній трикутник.
27 : 3 = 9 (см) – довжина сторони рівностороннього трикутника.
Відповідь: PK = 9 см.
Вправи для повторення
Завдання 315
На прямій позначено вісім точок так, що відстань між кожними двома сусідніми точками – однакова. Відстань між крайніми точками дорівнює 112 см. Знайдіть відстань між двома сусідніми точками.
Між 8 точками на прямій є 7 частин між сусідніми точками.
112 : 7 = (70 + 42) : 7 = 16 (см)
Відстань між сусідніми точками 16 сантиметрів.
Завдання 316
Розгорнутий кут поділили променями на три кути, один з яких удвічі менший від другого і втричі менший від третього. Знайдіть градусні міри цих трьох кутів.
Градусна міра розгорнутого кута дорівнює 180°.
Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається.
Нехай х (°) – перший найменший кут, тоді 2х (°) – другий кут, 3х (°) – третій кут. Складемо рівняння.
х + 2х + 3х = 180
6х = 180
х = 180 : 6
х = 30 (°) – перший кут.
2х = 30 • 2 = 60 (°) – другий кут.
3х = 30 • 3 = 90 (°) – третій кут.
Відповідь: 30°, 60°, 90°.
Життєва математика
Завдання 317
1) Скільки цегли і розчину потрібно для спорудження стіни 20 м завдовжки, 50 см (0,5 м) завтовшки і 2,5 м заввишки, якщо на 1 м3 кладки потрібно 400 цеглин, а витрати розчину становлять 20% від обсягу кладки?
Короткий запис
Довжина — 20 м
Ширина — 0,5 м
Висота — 2,5 м
V — ? м3
1) V = 20 • 0,5 • 2,5 = 25 (м3) – обсяг кладки.
Короткий запис
1 м3 — 400 ц.
25 м3 — ? ц.
Розчин — 20% від 25 м3
2) 400 • 25 = 10 000 (ц.) – цеглин потрібно.
3) 25 : 100 • 20 = 5 (м3) – обсяг розчину.
Відповідь: потрібно 10 000 цеглин і 5 м3 розчину.
2) Скільки коштуватимуть матеріали, якщо вартість однієї цеглини дорівнює 4,2 грн, а 1 м3 розчину – 1520 грн ?
Короткий запис
Цегла — 10 000 ц. по 4,2 грн
Розчин — 5 м3 по 1520 грн
Всього — ? грн
1) 4,2 • 10 000 = 4 200 (грн) – вартість цегли.
2) 1520 • 5 = 7 600 (грн) – вартість розчину.
3) 4 200 + 7 600 = 11 800 (грн) – вартість матеріалів.
Відповідь: вартість матеріалів 11 800 гривень.
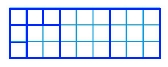
Завдання 318 Розріжте прямокутник, одна сторона якого дорівнює 3 клітинки, а друга – 9 клітинок, на вісім квадратів так, щоб розрізи проходили по сторонах клітинок.