ГДЗ математика 3 клас Гісь Філяк Урок 99, 100, 101 до підручника

Інші завдання дивись тут...

Серія "Вчимось разом" до підручника "Математика 3 клас Гісь О., Філяк І."

Урок 99

Завдання 1

1) Сума розрядних доданків: 135 = 100 + 30 + 5, 279 = 200 + 7 + 9 (істинне)

2) 4 • (9 + 2) = 4 • 9 + 4 • 2 (істинне)

3) 5 • 19 ≠ 5 • (10 + 9) (хибне)

4) Добуток зміниться від перестановки множників (хибне).

5) Якщо ціну помножити на кількість товару, то отримаємо вартість товару (істинне).

6) Якщо загальну довжину помножити на кількість відрізків, то одержимо довжину одного відрізка (хибне)

7) Якщо спільно чистити картоплю, то швидше почиститься уся картопля.

Завдання 2

Числа в порядку зростання суми їхніх цифр: 310, 140, 26, 19

^{2 + 6 = 8 1 + 4 + 0 = 5 3 + 1 + 0 = 4 1 + 9 = 10}

Збільшили кожне число у 3 рази (помножили на число 3):

310 • 3 = (300 + 10) • 3 = 300 • 3 + 10 • 3 = 900 + 30 = 930

140 • 3 = (100 + 40) • 3 = 100 • 3 + 4 • 3 = 300 + 120 = 420

26 • 3 = (20 + 6) • 3 = 20 • 3 + 6 • 3 = 60 + 18 = 78

19 • 3 = (10 + 9) • 3 = 10 • 3 + 9 • 3 = 30 + 27 = 57

Завдання 3

Завдання 4

^{242 • 3}

^{1) 242 = 200 + 40 + 2}

^{2) 242 • 3 = (200 + 40 + 2) • 3 = 200 • 3 + 40 • 3 + 2 • 3}

^{3) 600 + 120 + 6 = 726}

^{3 • 242}

^{1) 242 = 200 + 40 + 2}

^{2) 3 • 242 = 3 • (200 + 40 + 2) = 3 • 200 + 3 • 40 + 3 • 2}

^{3) 600 + 120 + 6 = 726}

Завдання 5 Розподільний закон множення відносно додавання

443 • 2 = (400 + 40 + 3) • 2 = 400 • 2 + 40 • 2 + 3 • 2 = 800 + 80 + 6 = 886

3 • 327 = 3 • (300 + 20 + 7) = 3 • 300 + 3 • 20 + 3 • 7 = 900 + 60 + 21 = 981

265 • 3 = (200 + 60 + 5) • 3 = 200 • 3 + 60 • 3 + 5 • 3 = 600 + 180 + 15 = 795

4 • 225 = 4 • (200 + 20 + 5) = 4 • 200 + 4 • 20 + 4 • 5 = 800 + 80 + 20 = 900

217 • 4 = (200 + 10 + 7) • 4 = 200 • 4 + 10 • 4 + 7 • 4 = 800 + 40 + 28 = 868

5 • 132 = 5 • (100 + 30 + 2) = 5 • 100 + 5 • 30 + 5 • 2 = 500 + 150 + 10 = 660

185 • 5 = (100 + 80 + 5) • 5 = 100 • 5 + 80 • 5 + 5 • 5 = 500 + 400 + 25 = 925

7 • 114 = 7 • (100 + 10 + 4) = 7 • 100 + 7 • 10 + 7 • 8 = 700 + 70 + 28 = 798

124 • 8 = (100 + 20 + 4) • 8 = 100 • 8 + 20 • 8 + 4 • 8 = 800 + 160 + 32 = 992

Завдання 6

^{1) Складена задача на знаходження суми}

За хвилину діти надувають 5 кульок. Спочатку вони надули 35 кульок. Ще 14 хв пішло на прив'язування ниток і вдвічі більше часу — на прикрашання кульками шкільного подвір'я. Скільки всього часу тривала робота дітей?

^{Короткий запис}

^{Надування кульок —}^?^{хв, 35 кульок уміщає по 5 кульок}

^{Прив’язування ниток — 14 хв}

^{Прикрашання подвір’я —}^?^{, у 2 рази більше, ніж прив’язування ниток}

^{Всього —}^?

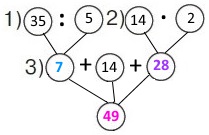
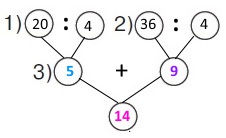
^{Вираз 35 : 5 + 14 + 14 • 2}

^{План розв’язування}

^{1) Скільки хвилин надували кульки діти?}

^{2) Скільки часу пішло на прикрашання подвір’я?}

^{3) Скільки всього часу тривала робота дітей?}

Розв’язання

1) 35 : 5 = 7 (хв.) – час на надування кульок.

2) 14 • 2 = 14 + 14 = 28 (хв.) – час на прикрашання подвір’я.

3) 7 + 14 + 28 = 49 (хв.) – всього часу тривала робота дітей.

Відповідь: робота дітей тривала 49 хвилин.

^{2) Складена задача з непов’язаними запитаннями}

У дітей є 24 пачки білої крейди, по 8 шматочків крейди у кожній, та 9 пачок кольорової крейди, по 11 шматочків крейди у кожній. Скільки всього шматочків крейди у дітей? На скільки шматочків білої крейди більше, ніж кольорової?

^Крейда	^{Шматочків у 1 пачці}	^{Кількість пачок}	^{Загальна кількість шматочків}
^Біла	⁸	²⁴	^?^{, на}^?^{шматочків більше}	^?
^{Кольорова}	¹¹	⁹	^?	^?

^{Короткий запис}

^{Біла —}^?^{шм., 24 пачки по 8 шматочків; на}^?^{шматочків більше}

^{Кольорова —}^?^{шм., 9 пачок по 11 шматочків}

^{Всього —}^?

^{План розв’язування}

^{1) Скільки шматочків білої крейди у дітей?}

^{2) Скільки шматочків кольорової крейди у дітей?}

^{3) Скільки всього шматочків крейди у дітей?}

^{4) На скільки шматочків білої крейди більше, ніж кольорової?}

Розв’язання

1) 8 • 24 = 8 • (20 + 4) = 192 (шм.) – шматочків білої крейди.

2) 11 • 9 = 90 + 9 = 99 (шм.) – шматочків кольорової крейди.

3) 192 + 99 = 100 + 180 + 11 = 291 (шм.) – всього шматочків крейди у дітей.

4) 192 – 99 = 192 – 100 + 1 = 93 (шм.) – на стільки шматочків білої крейди більше, ніж кольорової.

Відповідь: 291 шматок, на 93 шматочки більше.

^{3) Складена задача на зведення до одиниці}

Директор школи роздав шістьом класам 42 баночки з мильними бульбашками, порівну кожному. А кожному першому класу дав на 2 баночки більше. Скільки баночок із мильними бульбашками отримали 3 перші класи?

^{Баночок 1 класу}	^{Кількість класів}	^{Загальна кількість баночок}
^?	⁶	⁴²
^?^{, на 2 баночки більше}	³	^?

^{Короткий запис}

^{6 класів — 42 баночки, 1 клас —}^?^{баночок}

^{3 класам —}^?^{баночок, 1 хв —}^?^{, на 2 баночки більше}

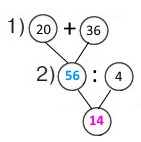
^{Вираз (42 : 6 + 2) • 3}

^{План розв’язування}

^{1) Скільки баночок з бульбашками отримав кожен із шістьох класів?}

^{2) Скільки баночок з бульбашками отримав кожний перший клас?}

^{3) Скільки баночок із мильними бульбашками отримали три перші класи?}

Розв’язання

1) 42 : 6 = 7 (б.) – баночок з бульбашками отримав кожен із шістьох класів.

2) 7 + 2 = 9 (б.) – баночок з бульбашками отримав кожний перший клас.

3) 9 • 3 = 27 (б.) – баночок із мильними бульбашками отримали три перші класи.

Відповідь: перші три класи отримали 27 баночок із мильними бульбашками.

Завдання 7 Склали 10 рівнянь із числами 27 і 3 та змінною f

f • 3 = 27

f = 27 : 3

f = 9

3 • f = 27

f = 27 : 3

f = 9

3 • f = 27 : 3

3 • f = 9

f = 9 : 3

f = 3

27 : f = 3

f = 27 : 3

f = 9

f : 3 = 27

f = 27 • 3

f = 81

27 : f = 3 • 3

27 : f = 9

f = 27 : 9

f = 3

f – 27 = 3

f = 3 + 27

f = 30

f – 3 = 27

f = 27 + 3

f = 30

27 – f = 3

f = 27 – 3

f = 24

3 + f = 27

f = 27 – 3

f = 24

f + 3 = 27

f = 27 – 3

f = 4

Завдання 8 Яке найбільше число можна дібрати замість k, щоб нерівність 9 • k < 44 була правильною?

^{Використаємо метод добору. 9 • 5 = 45, 45 > 44, число 5 не підходить. 9 • 4 = 36, 36 < 44, число 4 підходить.}

Відповідь: k = 4

Завдання 9

1) b • 6 > b • 3 у 2 рази

^{Міркуємо так. Спочатку b • 6 у 6 разів більше, ніж b. Якщо b збільшити у 3 рази, то перше число зменшиться у 3 рази, а в цілому збільшиться у 2 рази (6 : 3 = 2). Або (b • 6) : (b • 3) = (b • 3) • 2 : (b • 3) = (b • 3) : (b • 3) • 2 = 1 • 2 = 2 (рази)}

2) b • 6 > b : 4 у 24 рази

^{Міркуємо так. Спочатку b • 6 у 6 разів більше, ніж b. Якщо b зменшити у 4 рази, то перше число збільшиться ще у 4 рази, а в цілому збільшиться у 24 рази (6 • 4 = 24).}

Завдання 10

14 • 7 = (10 + 4) • 7 = 70 + 28 = 98

170 • 4 = (100 + 70) • 4 = 400 + 280 = 680

143 • 2 = (100 + 40 + 3) • 2 = 200 + 80 + 6 = 286

162 • 3 = (100 + 60 + 2) • 3 = 300 + 180 + 6 = 486

Урок 100

Завдання 1 Розподільний закон множення відносно додавання

Значення менше 640

Значення більше або рівне 640

^{5 • 127 = 5 • (100 + 20 + 7) = 500 + 100 + 35 = 635}

^{106 • 6 = (100 + 6) • 6 = 600 + 36 = 636}

^{8 • 55 = 8 • (50 + 5) = 8 • 50 + 8 • 5 = 400 + 40 = 440}

^{30 • 30 – 270 = 900 – 270 = 630}

^{170 • 4 = (100 + 70) • 4 = 400 + 280 = 680}

^{3 • 225 = 3 • (200 + 20 + 5) = 600 + 60 + 15 = 675}

^{2 • 320 = 2 • (300 + 20) = 600 + 40 = 640}

^{115 • 7 = (100 + 10 + 5) • 7 = 700 + 70 + 35 = 805}

^{8 • 109 = 8 • (100 + 9) = 800 + 72 = 872}

^{9 • 111 = 9 • (100 + 10 + 1) = 900 + 90 + 9 = 999}

^{70 • 80 + 95 = 5600 + 95 = 5695}

^{1000 – 810 : 9 = 1000 – 90 = 910}

У порядку спадання (від більшого до меншого): 636, 635, 630, 440

Завдання 2, 3

Сполучний закон множення: 4 • 2 • 3 = (4 • 2) • 3 = 4 • (2 • 3)

4 • 2 • 3 = 8 • 3 = 24 (4 • 2) • 3 = 8 • 3 = 24 4 • (2 • 3) = 4 • 6 = 24

^{Сполучний та переставний закони множення спрощують обчислення: 5 • 3 • 2 = (3 • 5) • 2 = 3 • (5 • 2) = 3 • 10 = 30}

Завдання 4 Обчислили зручним способом

3 • 4 • 5 = 3 • (4 • 5) = 3 • 20 = 60

5 • 7 • 6 = (5 • 6) • 7 = 30 • 7 = 210

10 • 9 • 8 = (9 • 8) • 10 = 72 • 10 = 720

8 • 7 • 5 = 7 • (8 • 5) = 7 • 40 = 280

Завдання 5 Віктор записав число 13. Уляна спочатку збільшила його удвічі, а тоді — ще утричі. Яке число одержала Уляна?

1) 13 • 2 • 3 = (10 + 3) • 2 • 3 = (20 + 6) • 3 = 60 + 18 = 78

2) 13 • (2 • 3) = 13 • 6 = (10 + 3) • 6 = 60 + 18 = 78

Завдання 6

10 • 60 = 60 • 10 переставний закон множення

105 + 92 = 92 + 105 переставний закон додавання

(m • n) • k = m • (n • k) сполучний закон множення

230 + 37 + 13 = 230 + (37 + 13) сполучний додавання

(30 • 2) • 5 = 30 • (2 • 5) сполучний закон множення

(a + b) + c = a + (b + c) сполучний закон додавання

b • c = c • b переставний закон множення

x + y = y + x переставний закон додавання

Завдання 7 Після пікніка хлопці можуть все прибрати за 12 хв, а дівчатка — за 8 хв. ^{Якщо діти прибиратимуть разом, їм знадобиться більше чи менше часу, ніж 12 хв?}

^{Міркуємо так. Якщо працюватимуть разом, тоді швидше впораються з роботою.}

Відповідь: знадобиться менше часу, ніж 12 хв; менше ніж 8 хв.

Завдання 8 Складена задача на ділення на вміщення

^{Стручки}	^{Квасолин у стручку}	^{Кількість стручків}	^{Загальна кількість квасолі}
^Великі	⁷	²¹	^?	¹⁹²
^Малі	⁵	^?	^?	¹⁹²

Усього — 192 квасолини. 21 великий стручок містив по 7 квасолин кожен. А в малих стручках було по 5 квасолин у кожному. Скільки малих стручків квасолі почистила мама?

^{Великі стручки}	^{Малі стручки}	^Всього
^{21 стручок по 7 квасолин}	^{? стручків по 5 квасолин}	^{192 квасолин}

^{Короткий запис}

^{Великі стручки —}^?^{кв., 21 стручок по 7 квасолин}

^{Малі стручки —}^?^кв.,^?^{стручків по 5 квасолин}

^{Всього — 192 квасолини}

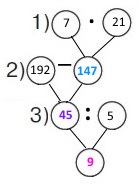
^{Вираз (192 – 7 • 21) : 5}

^{План розв’язування}

^{1) Скільки великої квасолі почистила мама?}

^{2) Скільки малої квасолі почистила мама?}

^{3) Скільки малих стручків квасолі почистила мама?}

Розв’язання

1) 7 • 21 = 7 • (20 + 1) = 147 (кв.) – великої квасолі почистила мама.

2) 192 – 147 = 50 – 5 = 45 (кв.) – малої квасолі почистила мама.

3) 45 : 5 = 9 (стр.) – малих стручків квасолі почистила мама.

Відповідь: мама почистила 9 малих стручків.

Завдання 9 Дві сестри принесли з городу 36 стручків гороху. Молодша сестра може почистити весь горох за 6 хв. Старша сестра може почистити весь горох за 9 хв.

Міркуємо так.

1) Якщо сестри чиститимуть горох разом, то їм потрібно для цього б) менше ніж б хвилин.

2) 36 : 6 = 6 (стр.) – стручків гороху чистить молодша сестра за 1 хвилину.

36 : 9 = 4 (стр.) – стручків гороху чистить старша сестра за 1 хвилину.

6 + 4 = 10 (стр.) – стручків гороху почистять дві сестри разом за 1 хвилину.

3) 10 • 3 = 30 (стр.) – стручків гороху почистять разом за 3 хв.

36 > 30 не встигнуть сестри разом почистити всі стручки за 3 хвилини.

10 • 4 = 40 (стр.) – стручків гороху почистять разом за 4 хв.

40 > 36 встигнуть сестри разом почистити всі стручки за 4 хвилини.

Завдання 10 Перший множник вибрати серед чисел 62, 85, 106, а другий множник серед чисел 5, 7, 9:

Добуток між 500 і 600

62 • 9 = (60 + 2) • 9 = 540 + 18 = 558

85 • 7 = (80 + 5) • 7 = 560 + 35 = 595

106 • 5 = (100 + 6) • 5 = 500 + 30 = 530

^{62 • 5 = (60 + 2) • 5 = 300 + 10 = 310}

^{62 • 7 = (60 + 2) • 7 = 420 + 14 = 434}

^{85 • 5 = (80 + 5) • 5 = 400 + 25 = 425}

^{85 • 9 = (80 + 5) • 9 = 720 + 45 = 765}

^{106 • 7 = (100 + 6) • 7 = 700 + 42 = 742}

^{106 • 9 = (100 + 6) • 9 = 900 + 54 = 954}

Завдання 11

Якщо m = 2, n = 113, тоді m + 4 • n = 2 + 4 • 113 = 2 + 452 = 454

(сума змінної m і добутку числа 4 на змінну n)

Якщо m = 2, n = 113, тоді (m + 4) • n = (2 + 4) • 113 = 6 • 113 = 678

(добуток суми змінної m і числа 4 на змінну n)

Цікавого у виразі: (m + 4) • n = m • n + 4 • n, m + 4 • n ≠ (m + 4) • n

(дужки змінюють значення виразу)

Завдання 12 Бабуся напекла булочок удвічі більше, ніж тістечок. Коли вона спекла ще 10 тістечок, булочок і тістечок стало порівну. Скільки булочок напекла бабуся?

^{Міркуємо так. Якщо бабуся напекла булочок удвічі більше, ніж тістечок, тоді булочок було 2 частини, а тістечок – 1 така частина. Якщо, коли вона спекла ще 10 тістечок, булочок і тістечок стало порівну, то їх стало по дві частини, тому 10 тістечок припадає на 1 частину, тому}

1) 10 • 2 = 20 (б.) – булочок напекла бабуся.

Відповідь: бабуся спекла 20 булочок.

Урок 101

Завдання 1

^{1) Із 10 полуниць з'їли першу і четверту (дві полуниці). Скільки залишилося?}

10 – 2 = 8 (п.)

^{2) Із 20 ґудзиків на сорочці відірвалися другий, третій і останній (три ґудзики). Скільки залишилося?}

20 – 3 = 17 (ґ.)

^{3) Зі 100 солдат у шерензі нагородили перших 10 і останніх 6 (шістнадцять солдатів). Скількох солдатів не нагороджено?}

100 – 16 = 84 (с.)

Завдання 2 Задача на знаходження чисел за трьома сумами

За три дні козачки подолали відстань 655 км. За перший і другий проїхали 422 км, а за другий і третій – 422 км. Скільки кілометрів козачки долали кожного дня?

^{Короткий запис}

^{I і ІІ — 422 км}

^{II і ІІІ — 422 км}

^{Всього — 655 км}

^{І —}^?^{, ІІ —}^?^{, ІІІ —}^?

Розв’язання

1) 655 – 422 = 233 (км) – кілометрів долали І дня.

2) 422 – 233 = 189 (км) – кілометрів долали ІІ дня.

3) 422 – 189 = 233 (км) – кілометрів долали ІІІ дня.

Відповідь: І день – 233 км, ІІ день – 189 км, ІІІ день – 233 км.

Завдання 3 Складена задача на знаходження суми часток

В одну бочечку за 4 хв налилося 20 л квасу, а в іншу бочечку — за той же час — 36 л квасу. Скільки літрів квасу за 1 хв налилося в обидві бочечки разом?

Розв’язання

^{1 спосіб}

^{Короткий запис}

^{І бочка —}^?^{хв., 20 літрів розділити на 4 порівну}

^{І бочка —}^?^{хв., 36 літрів розділити на 4 порівну}

^{Всього —}^?

^{Вираз 20 : 4 + 36 : 4}

Розв’язання

1) 20 : 4 = 5 (л) – літрів квасу наливалося у І бочку за 1 хвилину.

2) 36 : 4 = 9 (л) – літрів квасу наливалося у ІІ бочку за 1 хвилину.

3) 5 + 9 = 14 (л) – літрів квасу за 1 хв налилося в обидві бочечки разом.

^{2 спосіб}

^{Оскільки час однаковий, тому спочатку можна дізнатися кількість літрів за 4 хв, а потім за 1 хв, тоді}

^{Короткий запис}

^{І бочка за 4 хв — 20 літрів}

^{ІІ бочка за 4 хв — 36 літрів}

^{Всього (І і ІІ бочки за 4 хв) —}^?

^{І і ІІ бочка за 1 хв —}^?^{, у 4 рази менше}

^{Вираз (20 + 36) : 4}

Розв’язання

1) 20 + 36 = 56 (л) – літрів квасу налилося у дві бочки за 4 хвилини.

2) 56 : 4 = (40 + 16) : 4 = 14 (л) – літрів квасу наливалося у дві бочки за 1 хвилину.

Відповідь: у дві бочки разом за хвилину налилося 14 літрів квасу.

Завдання 4 Відчайдух може випити 6 л квасу за 2 хв, а Дзиґа — за 3 хв.

^{Козачки}	^{Літрів за 1 хв}	^{Кількість хвилин}	^{Загальна кількість літрів}
^{Відчайдух}	^?	²	⁶
^Дзиґа	^?	³	⁶
^Разом	^?	^?	¹⁰

^{Вираз 10 : (6 : 2 + 6 : 3)}

Розв’язання

1) Скільки літрів квасу випиває Відчайдух за 1 хвилину? 6 : 2 = 3 (л.)

2) Скільки літрів квасу випиває Дзиґа за 1 хвилину? 6 : 3 = 2 (л.)

3) Скільки літрів квасу випивають Відчайдух і Дзиґа разом за 1 хвилину? 3 + 2 = 5 (л.)

4) За скільки хвилин можуть випити 10 л квасу обоє козачків разом? 10 : 5 = 2 (хв)

Завдання 5 Обернена задача

Два козачки разом випили 10 л квасу за 2 хв. За скільки хвилин може випити 6 л квасу козачок Відчайдух, якщо Дзиґа може це зробити за 3 хв?

^{Козачки}	^{Літрів за 1 хв}	^{Кількість хвилин}	^{Загальна кількість літрів}
^{Відчайдух}	^?	^?	⁶
^Дзиґа	^?	³	⁶
^Разом	^?	²	¹⁰

^{Вираз 6 : (10 : 2 – 6 : 3)}

Розв’язання

1) 10 : 2 = 5 (л) – літрів квасу можуть випити обидва козачки разом за 1 хв.

2) 6 : 3 = 2 (л) – літрів квасу може випити Дзиґа за 1 хв.

3) 5 – 2 = 3 (л) – літрів квасу може випити Відчайдух за 1 хв.

4) 6 : 3 = 2 (хв) – треба хвилин.

Відповідь: випити шість літрів квасу Відчайдух може за 2 хв.

Завдання 6 Літр квасу коштує 10 грн. За першу бочку квасу заплатили 200 грн, а за другу — 300 грн. Скільки літрів квасу було в першій бочці і скільки — у другій?

^Бочки	^{Ціна (грн)}	^{Кількість}	^{Вартість (грн)}
^І	^{10 грн}	^?	^{200 грн}
^ІІ	^{10 грн}	^?	^{300 грн}

Розв’язання

1) 200 : 10 = 20 (л) – літрів квасу в І бочці.

2) 300 : 10 = 30 (л) – літрів квасу в ІІ бочці.

Завдання 7 Після подорожі Писар надіслав по Інтернету в Україну 320 листів, Відчайдух — на 40 листів менше, ніж Писар, а Дзиґа — у 3 рази менше, ніж Писар і Відчайдух разом. Скільки листів надіслав в Україну Дзиґа?

^{Короткий запис}

^{Писар — 320 листів}

^{Відчайдух —}^?^{, на 40 листів менше, ніж Писар}

^{Всього (Писар і Відчайдух разом) —}^?

^{Дзиґа —}^?^{, у 3 рази менше, ніж Писар і Відчайдух разом}