Відповіді до підручника Скворцова математика 4 клас сторінка 20

Інші завдання дивись тут...

© Барна Р., 2021

Серія "Вчимось разом" до підручника

"Математика 4 клас Скворцова С., Онопрієнко О."

Сторінка 20

Завдання 1 Змінили порядок виконання арифметичних дій, використавши дужки.

(64 + 32) : 8 – 9

(64 + 32) : (8 – 9)

64 + (32 : 8 – 9)

14 • (5 + 4) • 2

14 • (5 + 4 • 2)

(14 • 5 + 4) • 2

64 : (4 + 12) • 8

64 : (4 + 12 • 8)

(64 : 4 + 12) • 8

Завдання 2 Поставили дужки, щоб значення збільшилися:

6 • (12 + 8) 108 : (9 – 6) (45 + 21) • 9

Завдання 3

1) Задача на зведення до одиниці

На З однакових каруселях можуть одночасно покататися 15 дітей. Скільки дітей можуть покататися на 2 таких каруселях?

^{Короткий запис}

^{3 каруселі — 15 дітей}

^{2 каруселі — ? дітей}

Розв’язання

1) 15 : 3 = 5 (д.) – дітей на 1 каруселі.

2) 5 • 2 = 10 (д.)

Відповідь: можуть покататися 10 дітей.

_{Обернена задача на знаходження числа 2}

На З однакових каруселях можуть одночасно покататися 15 дітей. На скількох каруселях зможуть покататися 10 дітей?

^{Короткий запис}

^{3 каруселі — 15 дітей}

^{? каруселі — 10 дітей}

Розв’язання

1) 15 : 3 = 5 (д.) – дітей на 1 каруселі.

2) 10 : 5 = 2 (к.)

Відповідь: зможуть покататися на 2 каруселях.

2) Задача на послідовне множення

На каруселі одночасно можуть покататися 5 дітей. Скільки дітей можуть покататися на 2 таких каруселях за З рази?

^{Короткий запис}

^{1 карусель — 1 раз — 5 дітей}

^{2 каруселі — 3 рази —}^?^дітей

Розв’язання

1) 5 • 2 = 10 (д.) – дітей на 2 каруселях.

2) 10 • 3 = 30 (д.)– дітей на 2 каруселях за 3 рази.

^{2 спосіб}

^{1) 5 • 3 = 15 (д.) – дітей на 1 каруселі за 3 рази.}

^{2) 15 • 2 = 30 (д.) – дітей на 2 каруселях за 3 рази.}

Відповідь: за три рази на двох каруселях зможуть покататися 30 дітей.

_{Обернена задача на знаходження числа 3}

На каруселі одночасно можуть покататися 5 дітей. Скільки разів зможуть покататися на 2 таких каруселях 30 дітей?

^{Короткий запис}

^{1 каруселі — 1 раз — 5}^дітей

^{2 каруселі}^—^?^разів^{— 30 дітей}

Розв’язання

1) 5 • 2 = 10 (д.) – дітей на 2 каруселях.

2) 30 : 10 = 3 (рази) – разів зможуть покататися.

Відповідь: зможуть покататися 3 рази.

3) Складена задача

На одній каруселі одночасно можуть покататися 5 дітей, а на іншій — 7 дітей. Скільки дітей можуть покататися на обох каруселях за 3 рази?

^{Короткий запис}

^{1 карусель — 1 раз —}^?^{(5 дітей і 7 дітей)}

^{2 каруселі — 3 рази —}^?^дітей

Розв’язання

1) 5 + 7 = 12 (д.) – всього дітей на 2 каруселях.

2) 12 • 3 = 36 (д.) – дітей на 2 каруселях за 3 рази.

^{2 спосіб}

^{1) 5 • 3 = 15 (д.) – дітей на одній каруселі за 3 рази.}

^{2) 7 • 3 = 21 (д.) – дітей на другій каруселях за 3 рази.}

^{3) 15 + 21 = 36 (д.) – всього дітей на 2 каруселях.}

Відповідь: за три рази на двох каруселях зможуть покататися 36 дітей.

^{Обернена задача на знаходження числа 3}

На одній каруселі одночасно можуть покататися 5 дітей, а на іншій — 7 дітей. За скільки разів можуть покататися на обох каруселях 36 дітей?

^{Короткий запис}

^{1 карусель — 1 раз —}^?^{(5 дітей і 7 дітей)}

^{2 каруселі}^—^?^рази^{— 36 дітей}

Розв’язання

1) 5 + 7 = 12 (д.) – всього дітей на 2 каруселях.

2) 36 : 12 = 3 (рази) – разів можуть покататися діти.

Відповідь: діти зможуть покататися 3 рази.

Завдання 4

Мотузку завдовжки 13 м треба розрізати на дві частини так, щоб перша частина була на 5 м довша, ніж друга. Скільки метрів мотузки має бути в кожній частині?

Розв’язання

1) 13 – 5 = 8 (м) – подвійна довжина другої частини мотузки.

2) 8 : 2 = 4 (м) – довжина другої частини мотузки.

3) 4 + 5 = 9 (м) – довжина першої частини мотузки.

Відповідь: довжина першої частини 9 метри, другої – 4 метри.

Завдання 5 Полічи кількість твоїх вихідних днів восени.

Місяць	Кількість вихідних днів
вересень	8
жовтень	11
листопад	8
Усього	27

Сторінка 21

Завдання 1 Числові вирази

8 + 6 «сума чисел 8 і 6» 18 – 9 «різниця чисел 18 і 9»

8 • 6 «добуток чисел 8 і 6» 18 : 9 «частка чисел 18 і 9»

50 – 8 • 6 «від п’ятдесяти відняти добуток чисел 8 і 6»

(50 – 8) • 6 «різницю чисел 50 і 8 помножити на число 6»

Завдання 2

(16 • 8 + 232) : 40 • 67 = 603

1) 16 • 8 = (10 + 6) • 8 = 80 + 48 = 128

2) 128 + 232 = 360

3) 360 : 40 = 9

4) 9 • 67 = 67 • 9 = 67 • 10 – 67 = 603

(23 • 4 + 654 + 254) : 25 = 40

1) 23 • 4 = (20 + 3) • 4 = 92

2) 92 + 654 = 600 + 140 + 6 = 746

3) 746 + 254 = 746 + 300 – 46 = 1000

4) 1000 : 25 = 1000 : 100 • 4 = 40

(700 – 123 • 5) : 85 • 138 = 138

1) 123 • 5 = (100 + 20 + 30) • 5 = 615

2) 700 – 615 = 85

3) 85 : 85 = 1

4) 1 • 138 = 138

(129 + 963 : 3 + 180) : 5 = 126

1) 963 : 3 = (900 + 60 + 3) : 3 = 321

2) 129 + 321 = 450

3) 450 + 180 = 460 + 50 + 130 = 630

4) 630 : 5 = (500 + 100 + 30) : 5 = 126

Завдання 3 Порівняння чисел

480 + 240 – 360 < 900 – 670 + 190

^{(360 < 420)}

26 • 3 : 6 • 8 < 448 : 4 + 39

^{(34 < 151)}

(350 – 270) : 6 : 10 > (30 • 7 + 190) : 80

^{48 > 5}

51 : 17 • 19 > 43 – 64 : 16

^{(57 > 39)}

Завдання 4 Групи поданих математичних виразів

числові вирази

буквені вирази (вирази зі змінною)

51 : 17 • 8

100 • (64 : 16)

14 • (35 – 26)

а : 17 • 8

100 • (k : p)

14 • (р – 26)

Можемо одразу знаходити значення числових виразів:

51 : 17 • 8 = 3 • 8 = 24

100 • (64 : 16) = 100 • 4 = 400

14 • (35 – 26) = 14 • (35 – 25 – 1) = 14 • 9 = (10 + 4) • 9 = 126

Завдання 5

^{550 : 10 • 7 : 5 = 77}

^{1) 550 : 10 = 55}

^{2) 55 • 7 = (50 + 5) • 7 = 350 + 35 = 385}

^{3) 385 : 5 = (300 + 50 + 35) : 5 = 77}

^{(800 – 530) : 5 • 7 : 9 = 42}

^{1) 800 – 530 = 270}

^{2) 270 : 5 = (250 + 20) : 5 = 54}

^{3) 54 • 7 = (50 + 4) • 7 = 350 + 28 = 378}

^{4) 378 : 9 = (360 + 18) : 9 = 42}

^{7 • (136 – 98 + 12) : 5 = 70}

^{1) 136 – 98 = 38}

^{2) 38 + 12 = 50}

^{3) 7 • 50 = 350}

^{4) 350 : 5 = 70}

Завдання 6

68 : 34 • 2 • (26 + 24) = 68 : 34 • 2 • 50 = 2 • 2 • 50 = 4 • 50 = 200

^{1) 26 + 24 = 40 + 10 = 50}

^{2) 68 : 34 = 2}

^{3) 2 • 2 = 4}

^{4) 4 • 50 = 200}

112 : (84 : 12) • 8 = 112 : 7 • 8 = (70 + 42) : 7 • 8 = (10 + 6) • 8 = 80 + 48 = 128

^{1) 84 : 12 = 7}

^{2) 112 : 7 = (70 + 42) : 7 = 10 + 6 = 16}

^{3) 16 • 8 = (10 + 6) • 8 = 80 + 48 = 128}

(68 – 16) : 2 • 7 = 52 : 2 • 7 = (40 + 12) : 2 • 7 = (20 + 6) • 7 = 140 + 42 = 182

^{1) 68 – 16 = 52}

^{2) 52 : 2 = (40 + 12) : 2 = 20 + 6 = 26}

^{3) 26 • 7 = (20 + 6) • 7 = 140 + 42 = 182}

Сторінка 22

Завдання 1

Рівняння: 27 + х = 51

Нерівності зі змінною: 27 + х < 51 40 • р > 160

Завдання 2, 3

^{Щоб із чисел 1, 2, 4, 6, 12, 18 вибрати розв'язок рівняння або нерівності, можна методом добору підставити кожне і переконатися, що твердження істинне, або розв’язати.}

36 : х = 18

Якщо х = 1, тоді 36 : 1 = 36 – хибно.

Якщо х = 2, тоді 36 : 2 = 18 – істинно.

Відповідь: 2

а – 8 > 4

починаємо з числа, більшого за 8

якщо а = 12, тоді 12 – 8 > 4 – хибно

якщо а = 18, тоді 18 – 8 > 4 – істинно

Відповідь: 18

^{36 : х = 18}

^{х = 36 : 18}

^{х = 2}

^{а – 8 > 4}

^{а – 8 >12 – 8}

^{а > 12}

Завдання 4

36 : х = 18

36 : х = 36 : 2

х = 2

Відповідь: 2

а • 9 = 99

а • 9 = 11 • 9

а = 11

Відповідь: 11

51 : b = 17

51 : b = 51 : 3

b = 3

Відповідь: 3

р : 19 = 38

р : 19 = 722 : 19

р = 722

Відповідь: 722

k + 23 = 60

k + 23 = 37 + 23

k = 37

Відповідь: 37

Сторінка 23

Завдання 5

42 – k = 18

k = 42 – 18

k = 24

b + 26 = 70

b = 70 – 26

b = 44

n • 6 = 54

n = 54 : 6

n = 9

42 – k = 72 : 4

42 – k = 18

k = 42 – 18

k = 24

b + 13 • 2 = 70

b + 26 = 70

b = 70 – 26

b = 44

n • 6 = 540 : 10

n • 6 = 54

n = 54 : 6

n = 9

Завдання 2, 3 Розв'язування нерівностей у молодших класах

36 – а < 9

36 – а < 36 – 27

а > 27

Відповідь: 28, 29, …

72 + k > 80

72 + k > 72 + 8

k > 8

Відповідь: 9, 10, …

р + 26 < 50

р + 26 < 24 + 26

р < 24

Відповідь: 0, 1, ..

k – 27 > 18

k – 27 > 45 – 18

k > 45

Відповідь: 46, 47, ..

Завдання 4 Складена задача на знаходження невідомого доданку

Діти поїхали на екскурсію двома автобусами, по 25 дітей у кожному автобусі. Скільки поїхало дівчаток, якщо хлопчиків було 28?

^{Хлопчики}	^{Дівчатка}	^Всього
^{28 дітей}	^?	^{2 автобуси по 25 дітей}

^{Короткий запис}

^{Хлопчики — 28 дітей}

^{Дівчатка —}^?

^{Всього —}^?^{д., 2 автобуси по 25 дітей}

Розв’язання

Нехай х (д.) – дівчатка, тоді складемо рівняння

28 + х = 25 • 2

28 + х = 50

х = 50 – 28

х = 22 (д.)

^{2 спосіб}

^{1) 25 • 2 = 50 (д.) – всього дітей.}

^{2) 50 – 28 = 22 (д.) – дівчаток.}

Відповідь: поїхало 22 дівчаток.

Сторінка 24

Завдання 1 Ознайомлення з дробами

Дріб	1/2	1/8	1/6	1/4	1/3
Зафарбовано частин	1	1	1	1	1
Усього частин	2	8	6	4	3

Завдання 2, 3 Одиниці вимірювання

1) Яку частину метра становить 1 дм? 1 дм = 1/10 м

^{1 дм : 1 м = 1 дм : 10 дм = 1/10}

Яку частину метра становить 1 см? 1 см = 1/100 м

^{1 м : 1 см = 100 см : 1 см = 100}

2) Яку частину кілометра становить 1 м? 1 м = 1/1000 км

^{1 км : 1 м = 1000 м : 1 м = 1000}

3) Яку частину години становить 1 хв? 1 хв = 1/60 год

^{1 хв : 1 год = 1 хв : 60 хв = 1/60}

Яку частину години становить 1 с? 1 с = 1/3600 год

^{1 год = 60 хв = 1 хв • 60 = 60 с • 60 = 3600 с, тоді 1 с : 1 год = 1 с : 3600 с = 1/3600}

Завдання 4

1) 1 — ? км, 1/9 — 2 км 2 км • 9 = 18 км

1 — ? т, 1/12 — 7 т 7 т • 12 = 7 т • (10 + 2) = 70 т + 14 т = 84 т

1 — ? кг, 1/10 — 30 кг 30 кг • 10 = 300 кг

2) 1/5 від 1 км = 1 км : 5 = 1000 м : 5 = 200 м

1/20 від 1 ц = 1 ц : 20 = 100 кг : 20 = 5 кг

1/10 від 1 т = 1 т : 10 = 1000 кг : 10 = 100 кг

1/25 від 1 м = 1 м : 25 = 100 см : 25 = 100 см : 5 : 5 = 4 см

Завдання 5 Складена задача на знаходження невідомого доданку

На стоянці було 48 самокатів. Чверть усіх самокатів звичайні, а решта — електричні. Скільки електричних самокатів було на стоянці?

^{Короткий запис}

^{Звичайні —}^?^{, 1/4 від всього}

^{Електричні —}^?

^{Всього — 48 самокатів}

^Схема

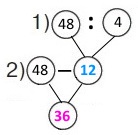
^{Вираз 48 – 48 : 4}

Розв’язання

1) 48 : 4 = (40 + 8) : 4 = 12 (с.) – звичайні самокати.

2) 48 – 12 = 36 (с.) – електричних самокатів було на стоянці.

Відповідь: на стоянці було 36 електричних самокатів.

Сторінка 25

Завдання 1

_{1) Задача на послідовне множення}

У центрі порятунку тюленів одній тварині на день дають 7 кг риби. Скільки кілограмів риби дадуть двом тюленям на тиждень (7 днів) за однакової норми годування?

^{Короткий запис}

^{1 тюлень — 1 день — 7 кг}

^{2 тюлені — 1 день —}^?^кг

^{7 тюлені — 7 днів —}^?^кг

^Схема

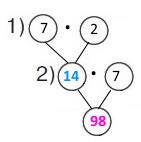
^{Вираз 7 • 2 • 7}

Розв’язання

1) 7 • 2 = 14 (кг) – риби дадуть 2 тюленям на 1 день.

2) 14 • 7 = (10 + 4) • 7 = 98 (кг) – риби дадуть 2 тюленям на 7 днів.

Відповідь: дадуть 98 кілограмів риби.

_{2) Задача на зведення до одиниці}

Двом тюленям на тиждень потрібно 98 кг риби. Скільки кілограмів риби потрібно трьом тюленям на тиждень за однакової норми годування?

^{Короткий запис}

^{2 тюлені — 98 кг}

^{3 тюлені — ? кг}

^Схема

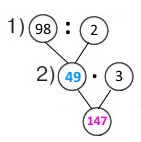
^{Вираз 98 : 2 • 3}

Розв’язання

1) 98 : 2 = (80 + 18) : 2 = 49 (кг) – риби потрібно 1 тюленю на тиждень.

2) 49 • 3 = (40 + 9) • 3 = 147 (кг) – риби потрібно 3 тюленям на тиждень.

Відповідь: потрібно 147 кілограмів риби.

_{3) Складена задача на різницеве порівняння часток}

Для тюленів у двох басейнах було встановлено різні добові норми споживання риби. У першому басейні двом тюленям на тиждень дають 98 кг риби, а в другому басейні трьом тюленям на тиждень дають 189 кг риби. У якому басейні один тюлень отримує щодня риби більше? На скільки більше?

Розв’язання

1) 98 : 2 : 7 = 49 : 7 = 7 (кг) – риби отримує тюлень щодня в І басейні.

2) 189 : 3 : 7 = 63 : 7 = 9 (кг) – риби отримує тюлень щодня в ІІ басейні.

3) 9 кг > 7 кг у другому басейні тюлень отримує більше риби щодня

9 – 7 = 2 (кг) – на стільки більше риби отримує тюлень в ІІ басейні щодня.

^{2 спосіб}

^{1) 98 : 2 = 49 (кг) – риби отримує тюлень щотижня в І басейні.}

^{2) 189 : 3 = 63 (кг) – риби отримує тюлень щотижня в ІІ басейні.}

^{3) 63 кг > 49 кг у другому басейні тюлень отримує більше риби щотижня}

^{63 – 49 = 63 – 50 + 1 = 14 (кг) – на стільки більше риби отримує тюлень щотижня в ІІ басейні.}

^{4) 14 : 7 = 2 (кг) – на стільки більше риби отримує тюлень щодня в ІІ басейні.}

Відповідь: на 2 кілограми більше риби отримує щодня тюлень в другому басейні.

Завдання 2

^{90 : 15 • 32 + 478 = 670}

^{1) 90 : 15 = 90 : (3 • 5) = 90 : 3 : 5 = 30 : 5 = 6}

^{2) 6 • 32 = 6 • (30 + 2) = 6 • 30 + 6 • 2 = 180 + 12 = 192}

^{3) 192 + 478 = 500 + 160 + 10 = 670}

^{40 : (72 : 18) • 83 + 136 = 966}

^{1) 72 : 18 = 72 : (9 • 2) = 72 : 9 : 2 = 8 : 2 = 4}

^{2) 40 : 4 = 10}

^{3) 10 • 83 = 830}

^{4) 830 + 136 = 966}

^{(49 + 84) : 19 • 32 – 126 = 98}

^{1) 49 + 84 = 120 + 13 = 133}

^{2) 133 : 19 = 7}

^{3) 7 • 32 = 7 • (30 + 2) = 210 + 14 = 224}

^{4) 224 – 126 = 224 – 124 – 2 = 98}

^{700 – 102 : 17 • 18 + 245 = 837}

^{1) 102 : 14 = 6}

^{2) 6 • 18 = 6 • (10 + 8) = 60 + 48 = 108}

^{3) 700 – 108 = 600 – 8 = 592}

^{4) 592 + 245 = 700 + 130 + 7 = 837}

^{22 : (140 – 129) • 72 – 86 = 58}

^{1) 140 – 129 = 140 – 130 + 1 = 11}

^{2) 22 : 11 = 2}

^{3) 2 • 72 = 2 • (70 + 2) = 140 + 4 = 144}

^{4) 144 – 86 = 144 – 90 + 4 = 58}

^{162 : (78 : 13) • 7 + 11 = 200}

^{1) 78 : 13 = 6}

^{2) 162 : 6 = (120 + 42) : 6 = 20 + 7 = 27}

^{3) 27 • 7 = (20 + 7) • 7 = 140 + 49 = 189}

^{4) 189 + 11 = 100 + 90 + 10 = 200}

Завдання 3

Якщо а = 17, тоді 34 : а + 38 : 2 = 34 : 17 + 38 : 2 = 2 + (20 + 18) : 2 = 2 + 19 = 21

Якщо b = 19, тоді 91 : 7 – 76 : b = 91 : 7 – 76 : 19 = (70 + 21) : 7 – 4 = 13 – 4 = 9

Завдання 4

240 : х = 91 – 88

240 : х = 3

х = 240 : 3

х = 80

240 : 80 = 3

91 – 88 = 3

3 = 3

4 • b = 37 + 47

4 • b = 84

b = 84 : 4

b = 21

4 • 21 = 84

37 + 47 = 84

84 = 84

с : (17 – 8) = 72

с : 9 = 72

с = 72 • 9

с = 648

648 : (17 – 8) = 648 : 9 = 72

72 = 72

(76 – 38) + k = 42

38 + k = 42

k = 42 – 38

k = 4

(76 – 38) + 4 = 38 + 4 = 42

42 = 42

b – 46 = 64 : 16

b – 46 = 4

b = 4 + 46

b = 50

50 – 46 = 4

64 : 16 = 4

4 = 4

t – 96 : 32 = 12

t – 3 = 12

t = 12 + 3

t = 15

15 – 96 : 32 = 15 – 3 = 12

12 = 12

Сторінка 26

Завдання 1 «Сусіди» числа — попереднє і наступне числа.

399, 400, 401 708, 709, 710 300, 301, 302

Завдання 2

Щоб одержати 500, треба 50 помножити на 10, бо 50 • 10 = 500

Щоб одержати 500, треба від 600 відняти 100, бо 600 – 100 = 500

Щоб одержати 500, треба 5 помножити на 100, бо 5 • 100 = 500

Завдання 3

^{180 + 230 = 400 + 110 = 510}

^{750 – 360 = 750 – 350 – 10 = 190}

^{800 – 490 = 800 – 500 + 10 = 310}

^{570 + 240 = 700 + 110 = 810}

^{140 • 5 = (100 + 40) • 5 = 520}

^{900 : 6 = (600 + 300) : 6 = 15}

Одержані результати в порядку зростання (від меншого до більшого):

15, 190, 310, 510, 520, 810

Завдання 4 Ділення з остачею

Числа, які можуть бути остачею під час ділення на 3: 1, 2

Числа, які можуть бути остачею під час ділення на 7: 4, 5, 6

Числа, які можуть бути остачею під час ділення на 10: 9

Завдання 5

Студент накопичує гроші на навушники, які коштують 1000 грн. У нього вже є половина суми. Скільки ще гривень потрібно накопичити студентові?

^{Короткий запис}

^{1 — 1000 грн}

^{1/2 — ?}

^Схема

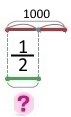
Розв’язання

^{Якщо в студента вже є половина суми, тоді йому треба накопичити ще половину суми, тому}

1000 : 2 = 500 (грн)

Відповідь: треба накопичити 500 гривень.

Завдання 6 Задачі на знаходження частини від числа

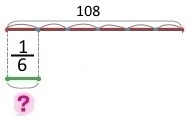
Торт коштує 108 грн. Скільки гривень треба заплатити за шосту частину торта?

^{Короткий запис}

^{Шматок — ? грн, 1/6 від 108 грн}

^Схема

Розв’язання

108 : 6 = (60 + 48) : 6 = 18 (грн)

Відповідь: за шосту частину торта треба заплатити 18 гривень.

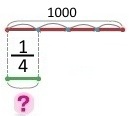
Маса торта 1 кг. Яка маса четвертини цього торта?

^{Короткий запис}

^{Четвертина — ? грн, 1/4 від 1 кг}

^Схема

Розв’язання

1 кг = 1000 г

1000 : 4 = (800 + 200) : 4 = 250 (г)

Відповідь: маса четвертини цього торта 250 г.

Інші завдання дивись тут...

Відповіді до підручника Скворцова математика 4 клас сторінка 20 – 26

Додавання коментаря