Інші завдання дивись тут...

© Барна Р., 2021

Серія "Вчимось разом" до підручника "Математика 3 клас Гісь О., Філяк І."

Урок 1  

Завдання 1  

На малюнку натуральні числа від 1 до 30: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30

 

Завдання 2

Полічили десятками до 100 (круглі числа від 10 до 100): 

10, 20, 30, 40, 50, 60, 70, 80, 90, 100

^{10 (найменше кругле число)   100 (найбільше кругле число)    50 (число, наступне за числом 49)    70 (число, попереднє до числа 71)}

 

Завдання 3 Сусіднє число до числа 1, яке не є натуральним

^{Міркуємо так. «Сусіди» числа 1 – це 0 і 2, 0 – не є натуральним числом.}

Відповідь: 0

 

Завдання 4 Серед чисел 0, 1, 2, 9, 10, 11, 30, 40, 45, 56, 67, 79, 98, 99 вибрали:

� найменше натуральне число — 1;

� найбільше одноцифрове число — 9;

� найбільше двоцифрове число — 99;

� найменше двоцифрове число — 10;

� число, що має «сусідів» 39 і 41 — 40;

� попереднє число від 80 — 79;

� наступне число за 29 — 30;

� число, що не є натуральним — 0;

� числа, що записані двома «сусідніми» цифрами і є більші ніж 50: 51 і 52

 

Завдання 5  Серед чисел 9, 11, 18, 23, 24, 26, 27, 32, 40, 45 вибрали:

парні числа 18, 24, 26, 32, 40      непарні числа: 9, 11, 23, 27, 45

 

Завдання 6

25 – двоцифрове непарне число, «сусід» чисел 24 і 26

90 – двоцифрове парне кругле число, «сусід» чисел 89 і 90

49 – двоцифрове непарне число, «сусід» чисел 48 і 50

2 – одноцифрове парне число, «сусід» чисел 1 і 3

 

Завдання 7

Числа першого десятка в порядку зростання: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

^{Міркуємо так. Числа першого десятку – 1, 2, 3, 4, 5, 6, 7, 8, 9 ,10, вони впорядковані в порядку зростання.}

Числа другого десятка в порядку спадання: 20, 19, 18, 17, 16, 15, 14, 13, 12, 11

^{Міркуємо так. Числа другого десятку – 11, 12, 13, 14, 15, 16, 17, 18, 19, 20. Впорядкуємо їх в порядку спадання – 20, 19, 18, 17, 16, 15, 14, 13, 12, 11}

Числа п’ятого десятка у прямому порядку (в порядку зростання):

41, 42, 43, 44, 45, 46, 47, 48, 49, 50

^{Міркуємо так. Числа п’ятого десятку – 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, вони впорядковані в порядку зростання (в прямому порядку).}

Числа шостого десятка у зворотному порядку (в порядку спадання):

60, 59, 58, 57, 56, 55, 54, 53, 52, 51

^{Міркуємо так. Числа шостого десятку – 51, 52, 53, 54, 55, 56, 57, 58, 59, 60. Впорядкуємо їх в порядку спадання (в зворотному порядку) – 60, 59, 58, 57, 56, 55, 54, 53, 52, 51.}

Парні числа восьмого десятка: 72, 74, 76, 78, 80

^{Міркуємо так. Числа восьмого десятку – 71, 72, 73, 74, 75, 76, 77, 78, 79, 80. Виберемо парні числа: 72, 74, 76, 78, 80.}

Непарні числа дев'ятого десятка: 81, 83, 85, 87, 89

^{Міркуємо так. Числа дев’ятого десятку – 81, 82, 83, 84, 85, 86, 87, 88, 89, 90. Виберемо непарні числа 81, 83, 85, 87, 89.}

  

Завдання 8  Скільки разів зустрілася цифра 9 у всіх числах десятого десятка?

^{Міркуємо так. Числа десятого десятка – 91, 92, 93, 94, 95, 96, 97, 98, 99, 100. Цифра 9 зустрічається 8 разів у числах від 91 до 98, ще 2 рази в числі 99, тоді разом 8 + 2 = 10 (разів)}

Відповідь: цифра зустрічається 10 разів.

 

Завдання 9 Ребуси

100ніжка – стоніжка, ті100 – тісто, пі2л – підвал, 100вп – стовп, 3зуб – тризуб, 100лиця – столиця, нами100 – намисто, 100рона – сторона, ві2га – відвага, г1а – година, 7'я – сім'я, 40а – сорока, напер100к – наперсток, мі100 – місто, ли100чок – листочок, р1а – родина, ві3на – вітрина

 

Урок 2 

Завдання 1 У школі 85 третьокласників.

97 — дев'яносто сім з математики.

84 — вісімдесят чотири з мови.

89 — вісімдесят дев'ять з читання.

76 —  сімдесят шість з природознавства.

Достатньо підручників з математики та читання (97 > 85, 89 > 85),

а недостатньо з мови та природознавства (84 < 85, 76 < 85).

 

Завдання 2

56 = 5 дес. 6 од.       38 = 3 дес. 8 од.      19 = 3 дес. 9 од.

64 = 6 дес. 4 од.       100 = 10 дес. = 1 сот.

100 – найбільше крейди оранжевого кольору

19 – найменше крейди зеленого кольору

 

Завдання 3 Групування розрядів у класи

Потрібно	Десятки	Одиниці	Число	Читаємо
Ложки	10		100	сто	10 дес.
Виделки	1		10	десять	1 дес.
Ножі кухонні		5	5	п’ять	5 од.
Тарілки мілкі	3	2	32	тридцять два	3 дес. 2 од.
Тарілки глибокі	2	3	23	двадцять три	2 дес. 3 од.
Склянки	8	4	84	вісімдесят чотири	8 дес. 4 од.

Числа в порядку зростання: 5, 10, 23, 32, 84, 100

 

Завдання 4

11	1) число другого десятка, у якого число одиниць до­рівнює числу десятків. Міркуємо так. Числа другого десятка: 11, 12, 13, 14, 15, 16, 17, 18, 19, 20. Серед них число, у якого число одиниць до­рівнює числу десятків:  11 = 1 дес. 1 од.
58	2) число між 50 і 60, у якого число одиниць на 3 більше, ніж число десятків Міркуємо так. Числа між 50 і 60 – це 51, 52, 53, 54, 55, 56, 57, 58, 59. Серед них 58 = 5 дес. 8 од. – число, у якого одиниць на 3 більше, ніж число десятків, бо 8 – 5 = 3.
42	3) число між 40 і 50, у якого число одиниць на 2 менше, ніж число десятків Міркуємо так. Числа між 40 і 50:  41, 42, 43, 44, 45, 46, 47, 48, 49, серед них 42 = 4 дес. 2 од., у нього число одиниць на 2 менше, ніж число десятків, бо 4 – 2 = 2.
30	4) число третього десятка, в якому число десятків на 3 більше, ніж число одиниць. Міркуємо так. Числа третього десятка: 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, серед них 30 = 3 дес. 0 од – число, у якого десятків на 3 більше, ніж число одиниць, бо 3 – 0 = 3.
69	5) число сьомого десятка, в якому число десятків на 3 менше, ніж число одиниць Міркуємо так. Числа сьомого десятка: 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, серед них 69 = 6 дес. 9 од. – число, у якого десятків на 3 менше, ніж одиниць, бо 9 – 6 = 3.

Завдання 5

30	24	45	33	36	62	22	98	40	87	14	54	65	18	76	99
А	Ж	І	Б	В	О	Р	И	В	Ь	Д	Р	Л	Е	П	Ш

1) непарні числа в порядку зростання

^{Міркуємо так. Непарні числа 45, 33, 87, 65, 99 впорядкуємо в порядку зростання.}

33, 45, 65, 87, 99 (більша)

2) парні числа, у яких число десятків менше 4

^{Міркуємо так. Парні числа 30, 24, 36, 62, 22, 98, 40, 14, 54, 18, 76. Серед них числа, у яких число десятків менше 4 – 30, 24, 36, 22, 14, 18, упорядкуємо в порядку зростання.}

14, 18, 22, 24, 30, 36 (держав)

3) парні числа, що більші, ніж 30, в яких число одиниць менше від числа десятків

^{Міркуємо так. Парні числа 30, 24, 36, 62, 22, 98, 40, 14, 54, 18, 76. Серед них числа більші від 30, в яких число одиниць менше від числа десятків – 62, 98, 40, 54, 76, упорядкуємо в порядку зростання.}

40, 54, 62, 76, 98 (вроп)

Україна – найбільша   держава Європи

 

Завдання 6 Порівняння натуральних чисел

� Порівняти 3 дес. і 9 од.             

3 дес. > 9 од.

^{Міркуємо так. 30 > 9, бо двоцифрові числа більші, ніж одноцифрові.}

� Порівняти 5 дес. 4 од. і 4 дес. 5 од.   

5 дес. 4 од. > 4 дес. 5 од.

^{Міркуємо так. Спочатку порівнюємо число десятків  5 д. > 4 д., тому 54 > 45.}

� Порівняти найменше кругле двоцифрове число і 1 дес. 1 од.

1 дес. < 1 дес. 1 од.

^{Міркуємо так. 10 – найменше кругле двоцифрове число. Попереднє число менше, ніж наступне, тому 10 < 11}

� Порівняти найбільше кругле двоцифрове число і 9 дес. 9 од.

9 дес. < 9 дес. 9 од.

^{Міркуємо так. Найбільше кругле двоцифрове число 90 = 9 дес., 90 < 99}

� Порівняти найбільше непарне число першого десятка і 9 дес.

9 од. < 9 дес.

^{Міркуємо так. Числа першого десятка 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, серед них найбільше непарне число – 9, одноцифрове число менше, ніж одноцифрове, тому 9 < 90.}

� Порівняти найменше парне число другого десятка і 20 дес.

1 дес. 2 од. < 20 дес.

^{Міркуємо так. Числа другого десятка 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, серед них парні – 12, 14, 16, 18, 20. З них найменше парне число – це 12 = 1 дес. 2 од., тому 1 дес. 2 од. < 20 дес.}

� Порівняти найменше непарне число третього десятка і 1 дес. 3 од.

2 дес. 1 од. > 1 дес. 3 од.

^{Міркуємо так. Числа третього десятка 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, з них непарні – 21, 23, 25, 27, 29. Найменше непарне число – це 21 = 2 дес. 1 од. Порівнюємо десятки 2 дес. > 1 дес., тому 2 дес. 1 од. > 1 дес. 3 од.}

� Порівняти найбільше парне число четвертого десятка і 4 дес.

4 дес. = 4 дес.

^{Міркуємо так. Числа четвертого десятка 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, серед них парні – це 32, 34, 36, 38, 40. Найбільше парне число – 40 = 4 дес., тому 4 дес. = 4 дес.}

 

Урок 3

Завдання 1

35	53	14	40	6
3 дес. 5 од.	5 дес. 3 од.	1 дес. 4 од.	4 дес.	6 од.

Числа в порядку зростання: 6, 14, 35, 40, 53

1) Додали два найбільші числа: 53 + 40 = 93

2) Відняли два найменші числа: 14 – 6 = 8

3) «Сума чисел 14 і 6 дасть 20»

«Різниця чисел 53 і 40 дорівнює тринадцяти».

4) Додали усі парні числа: 6 + 14 + 40 = 60

    доповнили суму до числа 100: 6 + 14 + 40 + 40 = 100

5)	Непарне число	два найближчі до нього круглі числа
	35	30,40
	53	50, 60

6) Три числа, у яких число десятків на 7 більше, ніж число одиниць:

70, 81, 92 (7 дес. 0 од., 8 дес. 1 од. 9 дес. 2 од.)

 

Завдання 2   

	3-А	3-Б	3-В
Хлопці	16	14	13
Дівчата	12	14 (стільки ж, скільки хлопців)	15 (на 2 учнів більше, ніж хлопців)
Всього	28	28	28

� Найбільше хлопців у 3-А класі (16)

� Найбільше дівчат у 3-В класі (15)

� Хлопців та дівчат порівну в 3-Б класі (14)

� Нема класу з найменшою кількістю учнів, бо у всіх класах учнів порівну

(16 + 12 = 14 + 14 = 13 + 15).

� 14 + 13 = 27 (хл.) – всього хлопців у 3-Б і в 3-В класах.

� 12 + 14 = 26 (д.) – дівчат разом у 3-А і 3-Б класах.

 

Завдання 3

1) 13 – 2 = 11 35 – 22 = 13 43 – 40 = 3

2) 29 – 7 = 12 10 + 13 = 23 3 + 16 = 16 + 3 = 19

3) 76 – 65 = 11 59 – 32 = 27 21 + 12 = 33

4) 94 – 70 = 24 19 – 4 = 15 62 – 41 = 21

5) 33 – 20 = 13 11 + 7 = 18 88 – 77 = 11

Київ – столиця України

 

Завдання 4  Складена задача на збільшення не деяке число і знаходження суми

Для наймолодших учнів школа придбала квитки до лялькового театру: 43 квитки – на виставу «Золоте курча», а на виставу «Попелюшка» – на 10 квитків більше. Скільки всього квитків до лялькового театру придбали для наймолодших школярів?

^{Короткий запис}

^{«Золоте курча» — 43 квитки}

^{«Попелюшка» — ?, на 10 квитків більше}

^{Всього — ?}

^Схема

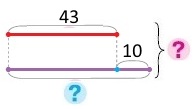
^{Вираз     43 + (43 + 10)}

Короткий запис №1 «Золоте курча» — 43 квитки «Попелюшка» — ?, на 10 квитків більше

Короткий запис №2 «Золоте курча» — 43 квитки «Попелюшка» — 53 квитки Всього — ?

^План

^{1) Скільки квитків придбала школа на виставу «Попелюшка»?}

^{2) Скільки всього квитків до лялькового театру придбала школа для наймолодших школярів?}

Розв’язання   

1) 43 + 10 = 53 (к.) – квитків на виставу «Попелюшка».

2) 43 + 53 = 96 (к.) – всього квитків до лялькового театру придбала школа для наймолодших школярів.

Відповідь: до лялькового театру для наймолодших школярів школа придбала 96 квитків.

 

Завдання 5

^{1) Складена задача на збільшення не деяке число і знаходження суми}

23 учні слухали екскурсовода на подвір'ї театру. А в музеї театру було на 3 учні більше. Скільки всього школярів прийшли до театру ляльок?

^{Короткий запис}

^{На подвір'ї — 23 школярі}

^{У музеї — ?, на 3 школярів більше}

^{Всього — ?}

Розв’язання   

1) 23 + 3 = 26 (шк.) – школярів було в музеї театру.

2) 23 + 26 = 49 (шк.) – всього школярів прийшли до театру ляльок.

Відповідь: до театру ляльок прийшло 49 школярів.

_{2) Складена задача на зменшення на деяке число}

Після екскурсії 25 школярів чекали у фойє театру. До гардеробу зайшло на 11 школярів менше, ніж чекало у фойє. До залу зайшло на 4 школярі менше, ніж до гардеробу. Скільки школярів зайшло до залу?

^{Короткий запис}

^{У фойє — 25 школярів}

^{У гардеробі — ?, на 11 школярів менше, ніж у фойє}

^{У залі — ?, на 4 школярі менше, ніж у гардеробі}

^Схема

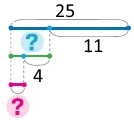
^{Вираз:   (25 – 11) – 4}

Короткий запис №1 У фойє — 25 школярів У гардеробі — ?, на 11 школярів менше

Короткий запис №2 У гардеробі — 14 школярів У залі — ?, на 4 школярі менше

^План

^{1) Скільки школярів зайшло до гардеробу?}

^{2) Скільки школярів зайшло до залу?}

Розв’язання     

1) 25 – 11 = 14 (шк.) – школярів зайшло до гардеробу.

2) 14 – 4 = 10 (шк.) – школярів зайшло до залу.

Відповідь: до залу зайшло 10 школярів.

 

Завдання 6

Числа на бейсболках	48	14	26	57	31
Імена дітей	Галя	Сашко	Андрій	Оля	Марко

^{Міркуємо так.}

^{1) Число Сашка має цифру 1 у розряді десятків, тому маємо число 14 = 1 дес. 4 од.}

^{2) Число Олі має число одиниць на 2 більше, ніж число десятків, тому маємо 57 = 5 дес. 7 од.}   

^{3) Число Марка є більшим, ніж число Андрія, але меншим, ніж число Галі. Оскільки число Марка є більшим, ніж число Андрія, тому маємо в порядку зростання число Андрія і Марка. Оскільки число Марка є меншим, ніж число Галі, тому маємо в порядку зростання числа Андрія, Марка, Галі. Числа, що залишились 48, 26, 31, упорядкуємо по зростанні, тоді 26, 31, 48, тому в Андрія – 26, у Марка – 31, в Галі – 48.}

 

Завдання 7

1) Із цифр 3, 6, 1, 8 додали найбільше і найменше можливі двоцифрові числа:

86 + 13 = 99

^{Міркуємо так. Із цифр 3, 6, 1, 8 найбільше двоцифрове число – 86 = 8 дес. 6 од., а найменше можливе  двоцифрове число – 13 = 1 дес. 3 од.}  

2) Відняли найбільше і найменше двоцифрові парні числа: 98 – 16 = 82

^{Міркуємо так. Із цифр 3, 6, 1, 8, 9 найбільше двоцифрове парне число – 98 = 9 дес. 8 од., а найменше двоцифрове парне число – 16 = 1 дес. 6 од.}

 

Урок 4 

Завдання 1 Рівняння

40 + 20 = 60 (бо 60 – 20 = 40) 90 – 50 = 40 (бо 90 – 40 = 50)	30 + 20 = 50 (бо 50 – 30 = 20) 60 – 10 = 50 (бо 50 + 10 = 60)	80 – 10 = 70 (бо 80 – 70 = 10) 90 – 20 = 70 (бо 70 + 20 = 90)
30 + 9 = 39 (бо 39 – 30 = 9) 8 + 70 = 78 (бо 78 – 8 = 70) 64 – 4 = 60 (бо 64 – 60 = 4)	60 + 4 = 64 (бо 64 – 4 = 60) 5 + 20 = 25 (бо 25 – 20 = 5) 45 – 5 = 40 (бо 40 + 5 = 45)	42 + 7 = 49 (бо 49 – 7 = 42) 4 + 23 = 27 (бо 27 – 4 = 23) 85 – 3 = 82 (бо 82 + 3 = 85)

Завдання 2  Додавання

1) 8 + 5 = 13 Додавання частинами: 8 + 5 = 8 + (2 + 3) = 8 + 2 + 3 = 10 + 3 = 13

2) 28 + 5 = 33 Додавання частинами: 28 + 5 = 28 + (2 + 3) = 28 + 2 + 3 = 30 + 3 = 33 Порозрядне додавання з переходом через десяток: 28 + 5 = (20 + 8) + 5 = 20 + (8 + 5) = 20 + 13 = 33

3)  28 + 15 = 43 Додавання частинами:   28 + 15 = 28 + (2 + 13) = 28 + 2 + 13 = 30 + 13 = 43,  28 + 15 = 28 + (10 + 5) = 28 + 10 + 5 = 38 + 5 = 43 Порозрядне додавання з переходом через десяток: 28 + 15 = (20 + 8) + (10 + 5) = (20 + 10) + (8 + 5) = 30 + 13 = 43

Завдання 3

9 + 6 = 9 + (1 + 5) = 9 + 1 + 5 = 10 + 5 = 15

12 + 8 = (10 + 2) + 8 = 10 + (2 + 8) = 10 + 10 = 20

31 + 9 = (30 + 1) + 9 = 30 + (1 + 9) = 30 + 10 = 40

53 + 8 = 53 + (7 + 1) = 53 + 7 + 1 = 60 + 1 = 61

14 + 16 = (10 + 10) + (4 + 6) = 20 + 10 = 30

47 + 26 = 47 + (3 + 20) = 47 + 3 + 23 = 50 + 23 = 73

 

Завдання 4   

^{Де більші доданки, там більша сума.}

1) 8 + 7 + 8 = 15 + 8 = 23        2) 34 + 16 + 22 = 50 + 22 = 72

 

Завдання 5 Віднімання

1) 13 – 7 = 6 Віднімання частинами: 13 – 7 = 13 – (3 + 7) = 13 – 3 – 4 = 10 – 4 = 6

2) 40 – 7 = 33 Порозрядне віднімання з переходом через десяток: 40 – 7 = (30 + 10) – 7 = 30 + (10 – 7) = 30 + 3 = 33

3) 43 – 7 = 36 Віднімання частинами: 43 – 7 = 43 – (3 + 4) = 43 – 3 = 4 = 40 – 4 = 36 Порозрядне віднімання з переходом через десяток: 43 – 7 = (30 + 13) – 7 = 30 + (13 – 7) = 30 + 6 = 36

4) 43 – 27 = 16 Віднімання частинами: 43 – 27 = 43 – (23 + 4) = 43 – 23 – 4 = 20 – 4 = 16                                   43 – 27 = 43 – (20 + 7) = 43 – 20 – 7 = 23 – 7 = 16

Завдання 6

12 – 5 = 12 – 2 – 3 = 7 15 – 7 = 15 – 5 – 2 = 8 40 – 8 = 30 + (10 – 8) = 32	80 – 6 = 70 + (10 – 6) = 74 60 – 36 = 20 + (40 – 36) = 24 30 – 12 = 18 + (12 – 12) = 18
40 – 36 = 4 92 – 9 = 92 – 2 – 7 = 83 55 – 8 = 55 – 5 – 3 = 47	42 – 16 = 42 – 12 – 4 = 26 64 – 47 = 64 – 44 – 3 = 17 36 – 28 = 36 – 20 – 8 = 8

Завдання 7

Числа	Рівність на віднімання	Рівність на додавання
4, 10, 15	15 – 10 = 5	4 + 15 = 19
16, 9, 8	16 – 8 = 16 – 6 – 2 = 8	16 + 9 = 25
9, 18, 35	35 – 9 = 35 – 5 – 4 = 26	35 + 18 = 35 + 15 + 3 = 53
12, 36, 60	60 – 12 = 60 – 10 – 2 = 48	36 + 12 = 48

Завдання 8  Проста задача на знаходження суми трьох доданків

У Києві побудовано три лінії метро. На лінії М1 працює 18 станцій, на лінії М2 – стільки ж, а на лінії М3 – 16 станцій. Скільки всього станцій метро працює у Києві?

^{Короткий запис}

^{Лінія М1 — 18 станцій}

^{Лінія М2 — 18 станцій (стільки ж, скільки на лінії М2)}

^{Лінія М3 — 16 станцій}

^{Всього — ?}

^Схема

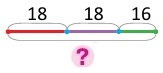
Розв’язання

18 + 18 + 16 = (18 + 2) + (18 + 2) + 12 = 20 + 20 + 12 = 52 (ст.) – всього станцій метро працює у Києві.

Відповідь: у Києві працює 52 станції метро.

 

Завдання 9 Складена задача на знаходження невідомого доданку (для більше двох доданків завжди має декілька способів розв'язування).

Ширина вулиці Хрещатик – 75 м. Проїжджа частина займає 24 м ширини всієї вулиці. Два тротуари мають ширину по 14 м кожний. Решту ширини вулиці займає алея з каштанами. Яка ширина алеї з каштанами?

Алея	Тротуар	Дорога	Тротуар	Всього
?	14 м	24 м	14 м	75 м

^{Короткий запис}

^{Алея — ?}

^{Тротуари — ?, 14 м і  14 м}

^{Дорога — 24 м}

^{Всього — 75 м}

^Схема

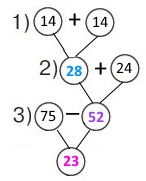
Вираз 75 – ((14 + 14) + 24)  

^План

^{1) Яка ширина двох тротуарів?}

^{2) Яка ширина тротуарів разом із проїжджою частиною?}

^{3) Яка ширина алеї з каштанами?}

Розв’язання  

1) 14 + 14 = 20 + 8 = 28 (м) – ширина двох тротуарів.

2) 24 + 28 = 24 + 6 + 22 = 52 (м) – ширина тротуарів разом із проїжджою частиною.

3) 75 – 52 = 23 (м) – ширина алеї з каштанами.

Відповідь: ширина алеї з каштанами 23 метри.

 

Завдання 10  

Правило: число останнього рядка – сума цифр початкового числа.

47	58	19	77	84	96	65	89	99
4 + 7	5 + 8	1 + 9	7 + 7	8 + 4	15 – 9	11 – 5	8 + 9	9 + 9
11	13	10	14	12	15	11	17	18

Урок 5

Завдання 1

^{Доданок + Доданок = Сума}

^{Щоб знайти невідомий доданок, треба від суми відняти відомий доданок.}

^{Зменшуване – Від’ємник = Різниця}

^{Щоб знайти зменшуване, треба до різниці додати від’ємник.}

^{Щоб знайти від’ємник, треба до різниці додати зменшуване.}

28 + 40 = 68 (бо 68 – 28 = 40) 20 + 32 = 52 (бо 52 – 32 = 20) 17 + 32 = 49 (бо 49 – 17 = 32) 54 + 34 = 88 (бо 88 – 34 = 54)

34 – 30 = 4 (бо 4 + 30 = 34) 79 – 53 = 26 (бо 26 + 53 = 79) 64 – 43 = 21 (бо 64 – 21 = 43) 87 – 74 = 13 (бо 87 – 13 = 74)

32 + 64 = 96 (2 од. + 4 од. = 6 од.,  9 дес. – 6 дес. = 3 дес.) 36 + 31 = 67 (7 од. – 1 од. = 6 од.,  6 дес. – 3 дес. = 3 дес.)  75 – 12 = 63 (5 од. – 3 од. = 2 од.,  7 дес. – 1 дес. = 6 дес.) 86 – 34 = 52 (6 од. – 2 од. = 4 од.,  5 дес. + 3 дес. = 8 дес.)

Завдання 2

Збільшити числа на 8 (додати число 8): 88 + 8 = 88 + 2 + 6 = 90 + 6 = 96 57 + 8 = 57 + 3 + 5 = 60 + 5 = 65 14 + 8 = 14 + 6 + 2 = 20 + 2 = 22 9 + 8 = 17

Зменшили числа на 23 (відняти число 23): 71 – 23 = 71 – 21 – 2 = 48 30 – 23 = 7 45 – 23 = 22 63 – 23 = 40

Завдання 3

^{Перший доданок на 2 більший, ніж другий (тобто другий доданок – на 2 менший, ніж перший)}

ІІ доданок	14 – 2 = 12	26 – 2 = 24	45 – 2 = 43	40 – 2 = 38
Сума	14 + 12 = 26	26 + 24 = 50	45 + 43 = 88	40 + 38 = 78
Рівності на віднімання	26 – 14 = 12 26 – 12 = 14	50 – 26 = 24 50 – 24 = 26	88 – 45 = 43 88 – 43 = 45	78 – 40 = 38 78 – 38 = 40

Завдання 4  Для різних доданків маємо «числові трійки»

7 + 5 = 12 5 + 7 = 12 12 – 5 = 7 12 – 7 = 5

11 + 9 = 20 9 + 11 = 20 20 – 11 = 9 20 – 9 = 11

43 + 8 = 51 8 + 43 = 51 51 – 43 = 8 51 – 8 = 43

6 + 94 = 100 94 + 6 = 100 100 – 6 = 94 100 – 94 = 6

Завдання 5  Для однакових доданків маємо «числові двійки»

23 + 23 = 46 46 – 23 = 23

35 + 35 = 70 70 – 35 = 35

25 + 25 = 50 50 – 25 = 25

47 + 47 = 94 94 – 47 = 47

Завдання 6

21 – 21 = 0  якщо зменшуване дорівнює від’ємнику, тоді різниця дорівнює нулю	52 – 30 = 20
12 – 11 = 1 різниця наступного і попереднього чисел дорівнює одиниці	59 – 45 = 14

Завдання 7 

Табір	«Сокіл»	«Едельвейс»	«Перлина»	«Лісовичок»	«Карпати»
Школярі	69	80	73	100	84

� Найбільше школярів (100 школярів) відпочивало в таборі «Лісовичок».

Найменше школярів (60 школярів) відпочивало в таборі «Сокіл».

� Серед школярів, що відпочивали в «Соколі», — 34 дів­чинки. Скільки хлопців відпочивало в «Соколі»?

69 – 34 = 35 (хл.) – хлопців відпочивало в «Соколі».

� 48 школярів приїхало в «Едельвейс» автобусом, а решта – поїздом. Скільки дітей приїхало в «Едельвейс» поїздом?

80 – 48 = 32 (д.) – дітей приїхало в «Едельвейс» поїздом.   

� Дев'ятьох дітей з «Перлини» батьки забрали трохи раніше. Скільки школярів відпочивало в «Перлині» до кінця зміни?

73 – 9 = 73 – 3 – 6 = 64 (шк.) –  школярів відпочивало в «Перлині» до кінця зміни.

� Скільки ще школярів мало би приїхати до табору «Карпати», щоб їхня кількість стала такою, як у таборі «Лісовичок»?

100 – 84 = 10 + (90 – 84) = 16 (шк.) – школярів мало би приїхати до табору «Карпати».

	З полуницею	З вишнею	З бананом
йогурт	46	34	20
морозиво	38	47	15

� 46 + 38 = 46 + 4 + 34 = 84 (шт.) – всього пачок йогуртів і порцій морозива з полуницею дали дітям на підвечірок.

� 34 + 47 = 34 + 6 + 41 = 81 (шт.) – всього пачок йогуртів і порцій морозива з вишнею дали дітям на підвечірок.

� 20 + 15 = 35 (шт.) – всього пачок йогуртів і порцій морозива з бананом дали дітям на підвечірок.

� 46 + 34 + 20 = 90 + 10 = 100 (п.) – всього пачок йогуртів дали дітям на підвечірок.

� 38 + 47 + 15 = 80 + 20 = 100 (п.) – всього порцій морозива дали дітям на під­вечірок.

 

Завдання 8

1) Число сьомого десятка, що має цифру 3 в розряді одиниць: 63

^{Міркуємо так. Числа сьомого десятка – 61, 62, 63, 64, 67, 68, 69, 70. Серед них число, що має цифру 3 в розряді одиниць  63 = 6 дес. 3 од.}

2) Число, у якого число десятків на 9 більше, ніж число одиниць: 90

^{Міркуємо так. 9 дес. 0 од. = 90}

Інші завдання дивись тут...