Відповіді 3 клас Заїка Математика Завдання 52 – 71 програма 2020 року Ответы ГДЗ до підручника Частина 2

Інші завдання дивись тут...

Серія "Вчимось разом" до підручника "Математика 3 клас Заїка А., Тарнавська С."

Завдання 52

380 – 200 = 180

420 – 100 = 320

520 – 100 = 420

620 – 100 = 520

530 – 300 = 230

250 – 70 = 250 – 50 – 20 = 180

350 – 70 = 350 – 50 – 20 = 280

450 – 70 = 450 – 50 – 20 = 380

250 – 90 = 250 – 50 – 40 = 160

360 – 80 = 360 – 60 – 20 = 280

460 – 80 = 460 – 60 – 20 = 380

560 – 80 = 560 – 60 – 20 = 480

Завдання 53 Проста задача на знаходження невідомого доданку

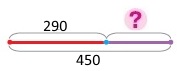
Автомобіліст протягом двох днів подолав 450 км. Першого дня він проїхав 290 км. Яку відстань подолав автомобіліст другого дня?

^{І день}	^{ІІ день}	^Всього
^{290 км}	^?	^{450 км}

^{Короткий запис}

^{І день — 290 км}

^{ІІ день — ?}

^{Всього — 450 км}

^Схема

Розв’язання

450 – 290 = 160 (км) – відстань подолав автомобіліст другого дня.

Відповідь: другого дня автомобіліст подолав 160 кілометрів.

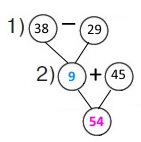
Завдання 54

Віднімання частинами:

450 – 290 = 450 – (200 + 90) = (450 – 200) – 90 = 250 – 90 = 160

Віднімання способом укрупнення розрядних одиниць:

450 – 290 = 45 дес. – 29 дес. = 16 дес. = 160

Віднімання способом округлення:

450 – 290 = 450 – (300 – 290) = 450 – 300 + 10 = 150 + 10 = 160

Завдання 55

640 – 380 = 640 – (340 + 40) = 640 – 340 – 40 = 300 – 40 = 260

640 – 70 = 64 дес. – 7 дес. = 64 дес. – 4 дес. – 3 дес. = 57 дес. = 570

340 + 90 = 340 + 60 + 30 = 400 + 30 = 430

180 + 180 = 180 + 20 + 160 = 200 + 160 = 360

Різниця між найбільшим і найменшим результатами: 590 – 260 = 330

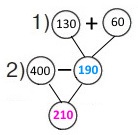
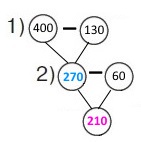
Завдання 56 Складена задача на віднімання суми від числа

У п'ятиповерховому паркінгу розміщено 400 автомобілів. До 9 год із паркінгу виїхало 130 автомобілів, з 9 до 12 год — ще 60. Скільки автомобілів залишилося опівдні в паркінгу?

1 спосіб

^{Короткий запис}

^{Було — 400 автомобілів}

^{Виїхало —}^?^{, 130 автомобілів і 60 автомобілів}

^{Залишилось —}^?

^{План розв’язування}

^{1) Скільки всього автомобілів виїхало?}

^{130 + 60 = 190 (ав.)}

^{2) Скільки автомобілів залишилося опівдні в паркінгу?}

^{400 – 190 = 210 (ав.)}

Розв'язання

400 – (130 + 60) = 210 (ав.)

2 спосіб

^{Оскільки спочатку виїхало декілька автомобілів, а потім ще декілька, тому}

^{Короткий запис}

^{Було — 400 автомобілів}

^{Виїхало спочатку — 130 автомобілів}

^{Залишились (Було) —}^?

^{Виїхало потім — 60 автомобілів}

^{Залишилось —}^?

^{План розв’язування}

^{1) Скільки автомобілів залишилося, коли виїхало 130?}

^{400 – 130 = 270 (ав.)}

^{2) Скільки автомобілів залишилося опівдні в паркінгу?}

^{270 – 60 = 210 (ав.)}

Розв’язання

(400 – 130) – 60 = 210 (ав.)

Відповідь: опівдні в паркінгу залишилося 210 автомобілів.

� Надлишкові дані: час до 9 год (спочатку, зранку), з 9 год до 12 год (потім, опівдні)

Завдання 57

а) Суму чисел 410 і 290 зменш на 40:

(410 + 290) – 40 = 700 – 40 = 660

б) Зменшуване 320, від'ємник — 90. Знайди різницю.

320 – 90 = 320 – 20 – 70 = 300 – 70 = 230

в) Від числа 370 відніми суму 110 і 180:

370 – (110 + 180) = 370 – 290 = 370 – 270 – 20 = 80

г) Різницю чисел 640 і 370 збільш на 300:

(640 – 370) + 300 = (640 – 340 – 30) + 300 = 270 + 300 = 570

Завдання 58 Прямокутник довжиною 6 см і шириною 4 см поділи на два рівні прямокутники.

^{Якщо поділимо по довжині 6 см, то будемо мати два прямокутники довжиною 4 см і шириною 3 см.}

^{Якщо поділимо по ширині 4 см, то матимемо два прямокутники довжиною 6 см і шириною 2 см.}

Обчислимо суму периметрів двох довших прямокутників.

1) Р = (6 + 2) • 2 = 16 (см) – периметр довшого прямокутника.

2) 16 + 16 = 32 (см) – сума периметрів двох довших прямокутників.

� Дослідили, чи буде сума периметрів менших прямокутників дорівнювати периметру великого прямокутника:

^{1) Р = (4 + 3) • 2 = 14 (см) – периметр меншого прямокутника.}

^{2) 14 + 14 = 28 (см) – сума периметрів двох менших прямокутників.}

^{3) Р = (6 + 4) • 2 = 20 (см) – периметр великого прямокутника.}

Ні, оскільки в сумі периметрів додатково двічі врахована сторона 4 см.

Завдання 59

12 – 5 = 12 – 2 – 3 = 7

120 – 50 = 12 дес. – 5 дес. = 7 дес. = 70

61 – 12 = 61 – 11 – 1 = 49

610 – 120 = 61 дес. – 12 дес. = 49 дес. = 490

63 – 15 = 63 – 13 – 2 = 48

630 – 150 = 480

54 – 38 = 54 – 34 – 4 = 16

540 – 380 = 160

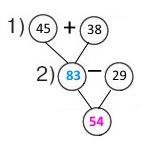
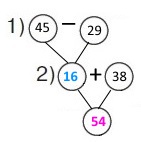
Завдання 60 Складена задача на додавання числа до суми

У першій коробці було 45 ялинкових іграшок, у другій — 38. На ялинку повісили 29 іграшок. Скільки іграшок залишилося у двох коробках?

1 спосіб

^{Короткий запис}

^{Було —}^?^{, 45 іграшок і 38 іграшок}

^{Повісили — 29 іграшок}

^{Стало —}^?

^{План розв’язування}

^{1) Скільки всього іграшок було в коробках?}

^{45 + 38 = 83 (іг.)}

^{2) Скільки іграшок залишилося у двох коробках?}

^{83 – 29 = 54 (іг.)}

Розв’язання

(45 + 38) – 29 = 54 (іг.)

2 спосіб

^{Нехай повісили іграшки з першої коробки, тоді}

^{Короткий запис}

^{Було в І коробці — 45 іграшок}

^{Повісили — 29 іграшок}

^{Залишилось (І коробка) —}^?

^{ІІ коробка — 38 іграшок}

^{Всього залишилось —}^?

^{План розв’язування}

^{1) Скільки іграшок залишилося у І коробці, коли взяли 29 іграшок?}

^{45 – 29 = 16 (іг.)}

^{2) Скільки іграшок залишилося у двох коробках?}

^{16 + 38 = 54 (іг.)}

Розв'язання

(45 – 29) + 38 = 54 (іг.)

^{3 спосіб}

^{Нехай повісили іграшки з другої коробки, тоді}

^{Короткий запис}

^{Було в ІІ коробці — 38 іграшок}

^{Повісили — 29 іграшок}

^{Залишилось (ІІ коробка) —}^?

^{І коробка — 45 іграшок}

^{Всього залишилось —}^?

^{План розв’язування}

^{1) Скільки іграшок залишилося у ІІ коробці, коли взяли 29 іграшок?}

^{38 – 29 = 9 (іг.)}

^{2) Скільки іграшок залишилося у двох коробках?}

^{9 + 45 = 54 (іг.)}

^{Розв'язання}

^{(38 – 29) + 45 = 54 (іг.)}

Відповідь: у двох коробках залишилось 54 іграшки.

Завдання 61 Яким математичним правилом можна пояснити дії продавчині, коли вона обчислює, яку решту дати з 400 грн після покупки на 290 грн?

^{Даю 10 грн здачі та ще 290 грн (за покупку) — це разом 300 грн. Щоб була загальна сума 400 грн, ще потрібно до 300 грн додати 100 грн, буде 400 грн. Отже, решта: 10 + 100 = 110 (грн).}

400 – 290 = 100 + (300 – 290) = 100 + 10 = 110 до числа додати різницю.

Завдання 62 «Родзинка» - додають і віднімають однакове число

^{Якщо деякого числа додати і відняти однакове число, то отримаємо початкове число.}

^{Якщо від деякого числа відняти і додати однакове число, то отримаємо початкове число.}

30 + 40 – 40 = 30 300 – 100 + 100 = 300

100 + 10 – 10 = 100 325 – 175 + 175 = 325

20 + 50 – 50 = 20 500 – 200 + 200 = 500

Завдання 63 Найближчі розрядні числа

70, 72, 80 300, 320, 400 400, 490, 500

Завдання 64 Зменшуване – Від’ємник = Різниця

^{Якщо зменшуване збільшити на декілька одиниць, тоді різниця також збільшиться на стільки ж одиниць:}

15 – 10 = 5

22 – 10 = (15 + 7) – 10 = (15 – 10) + 7 = 5 + 7 = 12

^{Якщо зменшуване зменшити на декілька одиниць, тоді різниця також зменшиться на стільки ж одиниць:}

120 – 30 = 90

100 – 30 = (120 – 20) – 30 = 120 – 20 – 30 = (120 – 30) – 20 = 90 – 20 = 70

380 – 180 = 200

320 – 180 = (380 – 60) – 180 = (380 – 180) – 60 = 200 – 60 = 140

Завдання64, 65 Порівняння чисел

100 – 30 < 110 – 30

^{де менше зменшуване, там менша різниця}

340 – 70 > 300 – 70

^{де більше зменшуване, там більша різниця}

76 – 15 < 80 – 15

^{де менше зменшуване, там менша різниця}

95 – 37 > 90 – 37

^{де більше зменшуване, там більша різниця}

Завдання 66

Додали і відняли однакове число:

450 – 370 = 450 + 20 – 370 – 20 = 470 – 370 – 20 = 100 – 20 = 80

Віднімання способом округлення:

450 – 370 = 450 – (400 – 30) = 450 – 400 + 30 = 50 + 30 = 80

530 – 180 = 530 – (200 – 20) = 530 – 200 + 20 = 330 + 20 = 350

Завдання 67 Складена задача на множення

Марійка й Дениско виготовляють браслети з бісеру. Марійка за 2 год зробила 6 браслетів, а Дениско — 4.

	^{Браслетів за 1 год} ^{(продуктивність праці)}		^Час	^{Загальна кількість браслетів}
^{Марійка}	^?		²	⁴
^{Дениско}	^?		²	⁶
^Разом		^?	²		^?

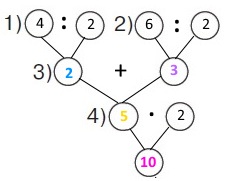
^{План розв’язування}

^{1) Скільки браслетів за 1 год виготовила Марійка?}

^{2) Скільки браслетів за 1 год виготовив Дениско?}

^{3) Скільки браслетів виготовили діти разом за 1 год?}

^{4) Скільки браслетів виготовили діти разом за 2 год?}

^{5) Хто працює спритніше?}

Розв’язання

6 : 2 = 3 (бр.) – браслетів за 1 год виготовила Марійка.

4 : 2 = 2 (бр.) – браслетів за 1 год виготовив Дениско.

3 + 2 = 5 (бр.) – браслетів виготовили діти разом за 1 год.

5 • 2 = 10 (бр.) – браслетів виготовили діти разом за 2 год.

3 > 2 Марійка працює спритніше

^{Спритніше працює той, хто виготовляє більше браслетів за одиницю часу (більша продуктивність праці)}

Чим захоплюєшся ти? Яке твоє хобі?...

Завдання 68

Обладнання для вимірювання на місцевості: землемірний циркуль (метр), сантиметрова стрічка, рулетка, далекомір.

а) Виміряй довжину й ширину шкільного подвір'я прямокутної форми

Довжина 300 м, ширина 100 м.

б) Обчислили довжину огорожі цього подвір'я (знайшли периметр прямокутника):

1 спосіб

Р = (300 + 100) • 2 = 400 • 2 = 800 (м)

^{2 спосіб}

^{Р = 300 • 2 + 100 • 2 = 600 + 200 = 800 (м)}

^{3 спосіб}

^{Р = 300 + 100 + 300 + 100 = 800 (м)}

Завдання 69 Порядок дій

^{2 • 8 + 10}^{= 16 + 10 =}²⁶

³²^:^{4 + 20}^{= 8 + 20 =}²⁸

^{470 – 100}^•³^{= 470 – 300 =}¹⁷⁰

^{240 – 5}^•⁸^{= 240 – 40 =}²⁰⁰

^{310 – 60}^{= 310 – 100 + 40 =}²⁵⁰

^{310 – 160}^{= 310 – 110 – 50 =}¹⁵⁰

Результати в порядку зростання (від меншого до більшого): 26, 28, 170, 150, 200, 250

Завдання 70 Задача на зведення до одиниці

У двох однакових пакетах 12 вафель. Скільки вафель у чотирьох таких пакетах? У трьох таких пакетах?

^{Вафель в 1 пакеті}	^{Кількість пакетів}	^{Загальна кількість вафель}
^?	²	¹²
^{однакова}	⁴	^?
^{однакова}	⁵	^?

Короткий запис

2 пакети — 12 вафель

^{1 пакет —}^?^вафель

4 пакети — ? вафель

5 пакетів — ? вафель

^{План розв’язування}

^{1) Скільки вафель у одному такому пакеті?}

^{2) Скільки вафель у чотирьох таких пакетах?}

^{3) Скільки вафель у трьох таких пакетах?}

Розв’язання

1 спосіб

1) 12 : 2 = 6 (в.) – вафель в одному пакеті.

2) 6 • 4 = 24 (в.) – вафель у чотирьох таких пакетах.

3) 6 • 3 = 18 (в.) – вафель у трьох таких пакетах.

^{2 спосіб}

^{1) 12 : 2 = 6 (в.) – вафель в одному пакеті.}

^{2) оскільки у 2 пакетах 12 вафель, а 4 пакети – це у 2 рази більше, ніж 2 пакети, то відповідно вафель у 2 рази більше тому}

^{12 • 2 = 24 (в.) – вафель у чотирьох таких пакетах.}

^{3) 6 • 3 = 18 (в.) – вафель у трьох таких пакетах.}

Завдання 71

Визнач, на якій відстані від школи проживає кожна дитина. Відомо, що Сергійко проживає на 200 м далі, ніж Галинка. Настуня проживає на 50 м ближче, ніж Петрик.

1 спосіб

Міркуємо так. Якщо Сергійко проживає на 200 м далі, ніж Галинка, тоді 950 – 750 = 200 (м.). Сергійко проживає на відстані 950 м, а Галинка – 750 м. Якщо Настуня проживає на 50 м ближче, ніж Петрик, тоді 960 – 910 = 50 (м). Настуня проживає на відстані 910 м, а Петрик – 960 м. Залишається Олег, котрий проживає на відстані 1000 м.

^{2 спосіб (табличний)}

^{750 м}	^{910 м}	^{950 м}	^{960 м}	^{1000 м}	^Умови
^{Галинка}		^{Сергійко}			^{Сергійко проживає на 200 м далі, ніж Галинка}
	^{Настуня}		^Петрик		^{Настуня проживає на 50 м ближче, ніж Петрик}
				^Олег