ГДЗ робочий зошит 4 клас Листопад математика сторінка 61

Інші завдання дивись тут...

Серія "Вчимось разом" до робочого зошита "Математика 4 клас Листопад Н."

Сторінка 61

Завдання 1 Ознайомлення з дробами

^{3/7 від 6 км 230 м = 6 км 230 м : 7 • 3 = 6230 м : 7 • 3 = 2670 м = 2 км 670 м}

^{3/7 від 8 т 771 кг = 8 т 771 кг : 7 • 3 = 8771 кг : 7 • 3 = 3759 кг = 3 т 759 кг}

^{3/7 від 1638 грн = 1638 грн : 7 • 3 = 1638 грн}

_6230 | 7

56 890

_63

_8771 | 7

7 1253

_17

_37

_21

_1638 | 7

14 234

_23

_28

х 890

2670 (м) = 2 км 670 м

х1253

3759 (кг) = 3 т 759 кг

х234

1638 грн

Завдання 2 Частки перевірили діленням

14 м 95 см : 65 см = 1495 см : 65 см = 23

20 ц 16 кг : 48 кг = 2016 кг : 48 кг = 42

_1495 | 65

130 23

_195

195

Перевірка:

_1495 | 23

138 65

_115

115

_2016 | 48

192 42

_96

Перевірка:

_2016 | 42

192 48

_96

Завдання 3 Знайди за планом площу кожної ділянки, якщо їхня загальна площа становить 3600, причому довжина першої ділянки 50 м, а другої – 40 м.

1) 50 + 40 = 90 (м) – довжина загальної ділянки.

2) 3600 : 90 = 360 : 9 = 40 (м) – ширина загальної ділянки.

3) 50 • 40 = 2000 (м²) – площа першої ділянки.

4) 40 • 40 = 1600 (м²) – площа другої ділянки.

^{2 спосіб}

^{1) 50 + 40 = 90 (м) – довжина загальної ділянки.}

^{2) 3600 : 90 = 360 : 9 = 40 (м) – ширина загальної ділянки.}

^{3) 50 • 40 = 2000 (м2) – площа першої ділянки.}

^{4) 3600 – 2000 = 1600 (м2) – площа другої ділянки.}

Відповідь: І ділянка – 2000 м², ІІ ділянка – 1600 м²

Сторінка 62-63

Завдання 1 Одиниці вимірювання

Червоний

12 ц : 300 = 1200 кг : 300 = 1200 кг : 100 : 3 = 12 кг : 3 = 4 кг

80 г + 3 кг = 3 кг 080 г

670 г • 5 = (600 г + 70 г) • 5 = 3000 г + 350 г = 3 кг 350 г

Блакитний

570 г • 5 = (500 г + 70 г) • 5 = 2500 г + 350 г = 2850 г = 2 кг 850 г

2 кг 10 г : 3 = 2010 г : 3 = (1800 г + 210 г) : 3 = 600 г + 70 г = 670 г

12 т : 500 = 12000 кг : 500 = 12000 кг : 100 : 5 = 120 кг : 5 = (100 кг + 20 кг) : 5 = 24 кг

Зелений

1 кг 200 г • 5 = (1 кг + 200 г) • 5 = 5 кг + 1000 г = 5 кг + 1 кг = 6 кг

2 кг 400 г : 60 = 2400 г : 60 = 2400 г : 10 : 6 = 240 г : 6 = 40 г

6 кг : 40 = 6000 г : 40 = 6000 г : 10 : 4 = 600 г : 4 = (400 г + 200 г) : 4 = 100 г + 50 г = 150 г

Коричневий

225 г • 4= (200 г + 20 г + 5 г) • 4 = 800 г + 80 г + 20 г = 900 г

7 кг 350 г : 3 = 7350 г : 3 = (6000 г + 1200 г + 150 г) : 3 = 2000 г + 400 г + 50 г = 2 кг 450 г

3 кг : 25 = 3000 г : 25 = 3000 г : 5 : 5 = 600 г : 5 = (500 г + 100 г) : 5 = 100 г + 20 г = 120 г

Сторінка 64

Завдання 1

_39215 | 341

341 115

_511

341

_1705

1705

_11067 | 217

1085 51

_217

217

Завдання 2 Складена задача на ділення

3 двох міст, відстань між якими становить 1155 км, назустріч одна одній виїхали легкові автомобілі. Швидкість одного автомобіля — 80 км/год, а іншого — на 5 км/год більша. Через скільки годин автомобілі зустрінуться?

^{Автомобілі}	^{Швидкість (км/год)}	^{Час (год)}	^{Відстань (км/год)}
^І	⁸⁰
^ІІ	^?^{, на 5 км/год більше}
^Всього	^?	^?	¹¹⁵⁵

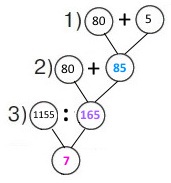
^{Вираз 1155 : (80 + (80 + 5))}

^{План розв’язування}

^{1) Яка швидкість другого автомобіля?}

^{2) Яка швидкість зближення?}

^{3) Через скільки годин автомобілі зустрінуться?}

Розв’язання

1) 80 + 5 = 85 (км/год) – швидкість другого автомобіля.

2) 80 + 85 = 80 + 20 + 65 = 165 (км/год) – швидкість зближення.

3) 1155 : 165 = 7 (год) – час зустрічі.

Відповідь: автомобілі зустрінуться через 7 год.

Завдання 3 Складена задача на ділення на вміщення

Майстер може зібрати 48 комплектів деталей за 4 год, а практикант — за 2 зміни по 6 год. За скільки годин виконають цю роботу майстер і практикант, якщо працюватимуть разом?

	^{Комплектів за 1 год} ^{(продуктивність праці)}	^{Кількість годин}	^{Загальна кількість комплектів}
^{Майстер}	^?	⁴	⁴⁸
^{Практикант}	^?	^?^{, 2 зміни по 6 год}	⁴⁸
^Всього	^?	^?	⁴⁸

^{Вираз 48 : (48 : 4 + 48 : (6 • 2))}

^{План розв’язування}

^{1) Скільки комплектів може зібрати майстер за 1 год? (Яка продуктивність праці майстра?)}

^{2) Скільки годин потрібно практикантові?}

^{3) Скільки комплектів може зібрати практикант за 1 год? (Яка продуктивність праці практиканта?)}

^{4) Скільки всього комплектів можуть зібрати майстер і практикант за 1 год разом?}

^{5) За скільки годин виконають цю роботу майстер і практикант, якщо працюватимуть разом?}

Розв’язання

1) 48 : 4 = (40 + 8) : 4 = 12 (к.) – комплектів може зібрати практикант за 1 год.

2) 6 • 2 = 12 (год) – годин потрібно практикантові.

3) 48 : 12 = 48 : 6 : 2 = 4 (к.) – комплектів може зібрати практикант за 1 год.

4) 12 + 4 = 16 (к.) – всього комплектів можуть зібрати майстер і практикант за 1 год разом.

5) 48 : 16 = 48 : 8 : 2 = 3 (год) – годин потрібно.

Відповідь: майстер і практикант разом виконають цю роботу за 3 години.

Сторінка 65

Завдання 1 Порядок дій

75 679 + (19 003 – 5773) : 315 = 75721

_19003

5773

13230

_13230 | 315

1260 42

_630

630

+75679

75721

Завдання 2 Рівняння

38092 : с + 747 = 836

38092 : с = 836 – 747

38092 : с = 89

с = 38092 : 89

с = 428

38092 : 428 + 747 = 89 + 747 = 836

836 = 836

Завдання 3 Складена задача на ділення на вміщення

Один насос наповнює басейн місткістю 1200 л за 20 хв, а інший — утричі повільніше (утричі більше хвилин). За скільки хвилин наповнять басейн ці два насоси, якщо працюватимуть разом?

^Насос	^{Літрів за 1 хв}	^{Час (хв)}	^{Загальна кількість літрів}
^І	^?	²⁰	¹²⁰⁰
^ІІ	^?	^?^{, 3 рази по 20}	¹²⁰⁰
^Разом	^?	^?	¹²⁰⁰

^{Вираз 1200 : (1200 : 20 + 1200 : (20 • 3))}

^{План розв’язування}

^{1) Скільки літрів води наповнює І насос за 1 хв?}

^{2) Скільки часу потрібно другому насосові?}

^{3) Скільки літрів води наповнює ІІ насос за 1 хв?}

^{4) Скільки літрів води наповнюють І і ІІ насос за 1 хв, якщо працюватимуть разом?}

^{5) За скільки хвилин наповнять басейн ці два насоси, якщо працюватимуть разом?}

Розв’язання

1) 1200 : 20 = 120 : 2 = 60 (л) – літрів води наповнює І насос за 1 хв.

2) 20 • 3 = 60 (хв) – часу потрібно другому насосові.

3) 1200 : 60 = 120 : 6 = 20 (л) – літрів води наповнює ІІ насос за 1 хв.

4) 60 + 20 = 80 (л) – літрів води наповнюють І і ІІ насос за 1 хв, якщо працюватимуть разом.

5) 1200 : 80 = 120 : 8 = (80 + 40) : 8 = 15 (хв) – хвилин потрібно для наповнення басейну.

Відповідь: наповнять басейн за 15 хвилин.

Сторінка 66

Завдання 1 Число є значенням частки чисел 5696 і 647: А 89

Завдання 2 Число є розв'язком рівняння b : 73 = 13462

Г 980 536

b : 73 = 13462

b = 13462 • 73

b = 980536

Завдання 3 За який час сухопутна черепаха подолає відстань 1 км 95м,якщо її швидкість становить 365 м/год?

Б 3 год

1 км 5 м = 1095 м, 1095 : 365 = 3 (год)

Завдання 4

4137 • 42 + 43 260 : 35 – 29 642 = 145348

х 4137

8274

16548

173754

_43260 | 35

35 1234

_82

_126

105

_210

210

+173754

1234

174990

_174990

29642

145348

Завдання 5 Складена задача на ділення на вміщення

У басейн місткістю 36 000 л занурено 2 насоси. Відомо, що перший насос може відкачати всю воду з басейна за 12 год, а другий — 6000 л за 1 год. За скільки годин відкачають усю воду два насоси, якщо працюватимуть разом?

^Насос	^{Літрів за 1 год}	^{Час (год)}	^{Загальна кількість літрів}
^І	^?	¹²	³⁶⁰⁰⁰
^ІІ	⁶⁰⁰⁰
^Разом	^?	^?	³⁶⁰⁰⁰

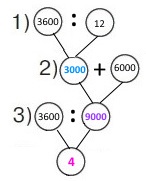
^{Вираз 36000 : (36000 : 12 + 6000)}

^{План розв’язування}

^{1) Скільки літрів води відкачує І насос за 1 год?}

^{2) Скільки всього літрів води відкачають І і ІІ насос за 1 год, якщо працюватимуть разом?}

^{3) За скільки годин відкачають усю воду два насоси, якщо працюватимуть разом?}

Розв’язання

1) 36000 : 12 = 3000 (л) – літрів води відкачує І насос за 1 год.

2) 3000 + 6000 = 9000 (л) – всього літрів води відкачають І і ІІ насос за 1 год, якщо працюватимуть разом.

3) 36000 : 9000 = 36 : 9 = 4 (год) – час для відкачки води.

Відповідь: насоси відкачають воду за 4 години.

Сторінка 67

Завдання 1 Натуральні числа в порядку збільшення:

531, 1235, 7867, 11528, 50001, 91200

Завдання 2 Установи закономірність і продовж кожний ряд

90 000, 80 000, 70 000, 60 000, 50 000, 40 000, 30 000

^{(наступне число на 10 000 менше, ніж попереднє).}

63 000, 62 000, 61 000, 60 000, 59 000, 58 000, 57 000

^{(наступне число на 10 000 менше, ніж попереднє).}

600 000, 60 000, 6 000, 600, 60, 6

^{(наступне число у 10 разів менше, ніж попереднє).}

Сторінка 68

Завдання 3

Вантажні машини	_{50 000}	^{150 000}	_{250 000}	^{350 000}	_{450 000}
Трактори	_{100 000}	^{200 000}	_{300 000}	^{400 000}	_{500 000}
Потяги	_{150 000}	^{250 000}	_{350 000}	^{450 000}	_{550 000}
Автомобілі	_{200 000}	^{300 000}	_{400 000}	^{500 000}	_{600 000}
Катери	_{250 000}	^{350 000}	_{450 000}	^{550 000}	_{650 000}

Сторінка 69

Завдання 5 Проста задача на знаходження невідомого доданку

Будівництво Дніпровської ГЕС у Запоріжжі розпочалось у 1927 році. Не повну потужність ГЕС запрацювала в 1939 році. Скільки років тривало будівництво станції?

^{Короткий запис}

^{Було — 1927 рік}

^{Тривало — ?}

^{Стало — 1939 рік}

Розв’язання

1939 – 1927 = 12 (років)

Відповідь: будівництво станції тривало 12 років.

Завдання 6

Ролики коштують 989 грн, а шолом – 379 грн. У кого з хлопчиків вистачить грошей на купівлю роликових ковзанів і захисного шолома?

+989

379

1368 (грн) – вартість цих двох товарів.

Денис має 1450 грн = 1000 грн + 200 грн • 2 + 50 грн

Павло має 1300 грн = 500 грн • 2 + 100 грн • 3

Селім має 1550 грн = 500 грн • 3 + 20 грн + 10 грн • 3

Обидва товари можуть купити Денис і Селім.

Сторінка 70

Завдання 7

З першої ділянки зібрали 25 мішків цибулі, а з другої — 33. Скільки кілограмів цибулі зібрали з кожної ділянки, якщо з першої зібрали на 200 кг менше, ніж із другої?

Ділянка	Маса 1 мішка (кг)	Кількість мішків	Загальна маса (кг)
І	?	25, на ? м. менше	?, на 200 кг менше
ІІ	однакова	33	?