© Барна Р., 2021
Серія "Вчимось разом" до підручника "Математика 4 клас Листопад Н. (частина 1)"
Завдання 174 Зменшили у 7 разів (поділили на число 7):
21 : 7 = 3 77 : 7 = 11 700 : 7 = 100 350 : 7 = 50 35 : 7 = 5 420 : 7 = 60
Завдання 175 Визначили, скільки в кожному числі всього сотень, усього десятків, усього одиниць:
|
Число |
125 |
804 |
328 |
390 |
777 |
522 |
|
Всього одиниць |
125 |
804 |
328 |
390 |
777 |
522 |
|
Всього десятків |
12 |
80 |
32 |
39 |
77 |
52 |
|
Всього сотень |
1 |
8 |
3 |
3 |
7 |
5 |
Завдання 176
266 : 7 = (210 + 56) : 7 = 210 : 7 + 56 : 7 = 30 + 8 = 38
Завдання 177 Визначили, у яких частках у результаті буде двоцифрове число.
288 : 6 перше неповне ділене 28 дасть 1 цифру і ще залишилась одна цифра, тому в частці 2 цифри.
783 : 9 перше неповне ділене 78 дасть 1 цифру і ще залишилась одна цифра, тому в частці 2 цифри.
505 : 5 перше неповне ділене 5 дасть 1 цифру і ще залишилось дві цифри, тому в частці 3 цифри.
376 : 4 перше неповне ділене 37 дасть 1 цифру і ще залишилась одна цифра, тому в частці 2 цифри.
856 : 8 перше неповне ділене 8 дасть 1 цифру і ще залишилось дві цифри, тому в частці 3 цифри.
Завдання 178 Ділення перевірили множенням
|
_696 | 8 64 87 _56 56 0 |
х 87 8 696 |
_261 | 3 24 87 _21 21 0 |
х 87 3 261 |
_462 | 7 42 66 _42 42 0 |
х 66 7 462 |
_198 | 2 18 99 _18 18 0 |
х 99 2 198 |
Завдання 179
|
315 : 5 + 135 = 63 + 135 = 198 336 + 336 : 7 = 336 + 48 = 384 (336 + 336) : 7 = 672 : 7 = 96 |
_315 | 5 30 63 _15 15 0 |
+135 63 198 |
_336 | 7 28 48 _56 56 0 |
+336 48 384 |
+336 336 672 |
_672 | 7 63 96 _42 42 0 |
Завдання 180
Дорогу завдовжки 72 км перша бригада може відремонтувати за 3 тижні, а друга — за 6 тижнів. За скільки тижнів відремонтують цю дорогу дві бригади, якщо працюватимуть разом?
|
Бригада |
Довжина за 1 тиждень (км) |
Кількість тижнів |
Загальна довжина (км) |
|
І |
? |
3 |
72 |
|
ІІ |
? |
6 |
однаково |
|
Разом |
? |
? |
72 |
Короткий запис
І бригада — 72 км за 3 тижні
ІІ бригада — 72 км за 6 тижнів
Разом — 72 км за ? тижнів
Схема
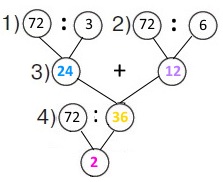
Вираз 72 : (72 : 3 + 72 : 6)
|
Короткий запис №1 І бригада — 72 км — це 3 тижні по ? км |
Короткий запис № 3 І бригада — 24 км ІІ бригада — 12 км Всього — ? |
|
Короткий запис №2 ІІ бригада — 72 км — це 6 тижнів по ? км |
Короткий запис №4 Разом — 72 км — це ? тижнів по 36 км |
План розв’язування
1) Скільки кілометрів дороги може відремонтувати за тиждень перша бригада?
2) Скільки кілометрів дороги може відремонтувати за тиждень друга бригада?
3) Скільки кілометрів дороги можуть відремонтувати за тиждень перша і друга бригади
разом?
4) За скільки тижнів відремонтують цю дорогу дві бригади, якщо працюватимуть разом?
Розв’язання
1) 72 : 3 = (60 + 12) : 3 = 24 (км) – І бригада за 1 тиждень;
2) 72 : 6 = (60 + 12) : 6 = 12 (км) – ІІ бригада за 1 тиждень;
3) 24 + 12 = 36 (км) – можуть відремонтувати дві бригади за 1 тиждень;
4) 72 : 36 = 2 (т.)
Відповідь: цю дорогу дві бригади відремонтують за 2 тижні.
Завдання 181
120 г сухого корму Рекс з’їдає за 3 дні, а Чапа — за 6 днів. На скільки днів їм обом вистачить цього корму?
|
Собаки |
Корму за 1 день (г) |
Кількість днів |
Загальна кількість корму (г) |
|
Рекс |
? |
3 |
120 |
|
Чапа |
? |
6 |
однаково |
|
Разом |
? |
? |
120 |
Короткий запис
Рекс — 120 г км за 3 дні
Чапа — 120 г за 6 днів
Разом — 120 г за ? днів
Схема
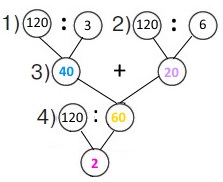
Вираз 120 : (120 : 3 + 120 : 6)
План розв’язування
1) Скільки корму з’їдає Рекс за день?
2) Скільки корму з’їдає Чапа за день?
3) Скільки корму з’їдають разом за день?
4) На скільки днів їм обом вистачить цього корму?
Розв’язання
1) 120 : 3 = 40 (г) – корму з'їдає за день Рекс;
2) 120 : 6 = 20 (г) – корму з'їдає за день Чапа;
3) 40 + 20 = 60 (г) – корму з'їдають за день разом;
4) 120 : 60 = 2 (дні)
Відповідь: корму вистачить на 2 дні.
Завдання 182
|
256 – 256 : 4 = 256 – 64 = 192 688 + 688 : 8 = 688 + 86 = 774 672 : 4 – 672 : 8 = 168 – 84 = 84 |
_256 | 4 24 64 _16 16 0 |
_256 64 192 |
_688 | 8 64 86 _48 48 0 |
+688 86 774 |
_672 | 4 4 168 _27 24 _32 32 0 |
_672 | 8 64 84 _32 32 0 |
_168 84 84 |
Завдання 183
Мама за 20 хв зліпила 40 вареників, а син за 10 хв — 10 вареників. Скільки вареників зліплять мама й син за 5 хв, якщо ліпитимуть їх разом?
|
|
Вареників за 1 хв |
Кількість хвилин |
Загальна кількість вареників |
|
Мама |
? |
20 |
40 |
|
Син |
? |
10 |
10 |
|
Разом |
? |
5 |
? |
Короткий запис
Мама — 40 вареників за 20 хв
Син — 10 вареників за 10 хв
Разом — ? вареників за 5 хв
Схема
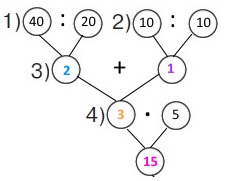
Вираз (40 : 20 + 10 : 10) • 5
|
Короткий запис №1 Мама 1 хв — ? вареників 20 хв — 40 вареників |
Короткий запис № 3 Мама — 2 вареники Син — 1 вареник Всього — ? |
|
Короткий запис №2 Син 1 хв — ? вареників 10 хв — 10 вареників |
Короткий запис №4 Разом 1 хв — 3 вареники 5 хв — ? вареників |
План розв'язування
1) Скільки вареників зліпила мама за 1 хвилину?
2) Скільки вареників зліпив син за 1 хвилину?
3) Скільки всього вареників зліпили мама і син разом за 1 хвилину?
4) Скільки вареників зліплять мама й син разом за 5 хвилин?
Розв’язання
1) 40 : 20 = 2 (в.) – зліпила мама за 1 хв;
2) 10 : 10 = 1 (в.) – зліпив син за 1 хв;
3) 2 + 1 = 3 (в.) – зліпили мама і син разом за 1 хв;
4) 3 • 5 = 15 (в.)
Відповідь: за п’ять хвилин мама і син разом зліплять 15 вареників.
Завдання 184
Зменшили утричі (поділили на число 3) парні числа:
108 : 3 = (90 + 18) : 3 = 36 366 : 3 = (300 + 60 + 6) : 3 = 122
714 : 3 = (600 + 90 + 24) : 3 = 238 60 : 3 = 20
Збільшили удвічі (помножили на число 2) непарні числа:
99 • 2 = 2 • 99 = 2 • 100 – 2 = 198 51 • 2 = (50 + 1) • 2 = 100 + 2 = 102 333 • 2 = (300 + 30 + 3) • 2 = 600 + 60 + 6 = 662
Завдання 185
721 : 7 = (700 + 21) : 7 = 700 : 7 + 21 : 7 = 100 + 3 = 103
Завдання 186
|
Перевірка письмовим множенням |
|||||||||
|
_812 | 4 8 203 _12 12 0 |
_918 | 3 9 306 _18 18 0 |
_612 | 2 6 306 _12 12 0 |
_612 | 3 6 204 _12 12 0 |
_612 | 6 6 102 _12 12 0 |
х203 4 812 |
х306 3 918 |
х306 2 612 |
х204 3 612 |
х102 6 612 |
Завдання 187
|
74 • 9 : 6 = 666 : 6 = 111 88 • 5 : 8 = 440 : 8 = 55 207 • 4 : 9 = 828 : 9 = 92 |
х74 9 666 |
_666 | 6 6 111 _6 6 _6 6 0 |
х88 5 440 |
_440 | 8 40 55 _40 40 0 |
х207 4 828
|
_828 | 9 81 92 _18 18 0 |
Завдання 188
|
(915 – 165) : 6 = 750 : 6 = 125 185 : 5 + 185 • 5 = 37 + 925 = 962 (269 + 147) : 4 = 416 : 4 = 104 3 • (1000 – 736) : 8 = 3 • 264 : 8 = 792 : 8 = 99 |
|||||||||
|
_750 | 6 6 125 _15 12 _30 30 5 |
_185 | 5 15 37 _35 35 0 |
х185 5 925 |
+925 37 962 |
+269 147 416 |
_416 | 4 4 104 _16 16 0 |
_1000 736 264 |
х264 3 792 |
_792 | 8 72 99 _72 72 0 |
|
Завдання 189 Рівняння
|
828 : х = 4 х = 828 : 4 х = 207 |
с • 7 = 714 с = 714 : 7 с = 102 |
6 • а = 372 а = 372 : 6 а = 62 |
_828 | 4 8 207 _28 28 0 |
_714 | 7 7 102 _14 14 0 |
_372 | 6 36 602 _12 12 0 |
Завдання 190
1) Перший насос може викачати 12 т води за 6 год, а другий — за 3 год. За скільки годин викачають цю воду два насоси, якщо працюватимуть разом?
Короткий запис
І насос — 12 т за 6 год
ІІ насос — 12 т за 3 год
Разом — 12 т за ? год
Схема
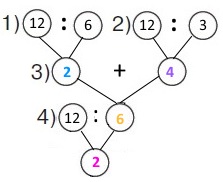
Вираз 12 : (12 : 6 + 12 : 3)
Розв’язання
1) 12 : 6 = 2 (т) – може викачати І насос за 1 год;
2) 12 : 3 = 4 (т) – може викачати ІІ насос за 1 год;
3) 2 + 4 = 6 (т) – можуть викачати разом за 1 год;
4) 12 : 6 = 2 (год)
Відповідь: два насоси викачають цю воду за 2 години.
2) Перший насос може викачати 12 т води за 6 год, а другий — за 3 год. За скільки годин ці насоси викачають 30 т води, якщо працюватимуть разом?
Короткий запис
І насос — 12 т за 6 год
ІІ насос — 12 т за 3 год
Разом — 30 т за ? год
Схема
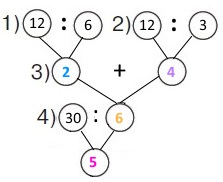
Вираз 30 : (12 : 6 + 12 : 3)
Розв’язання
1) 12 : 6 = 2 (т) – може викачати І насос за 1 год;
2) 12 : 3 = 4 (т) – може викачати ІІ насос за 1 год;
3) 2 + 4 = 6 (т) – можуть викачати разом за 1 год;
4) 30 : 6 = 5 (год)
Відповідь: два насоси викачають цю воду за 5 годин.
� Спільне: однаковий тип задачі, однакові дії.
Відмінне: перше ділене у четвертій дії.
Завдання 191 Побудуй прямокутник, довжина якого дорівнює 8 см, а ширина становить 1/2 довжини. Обчисли його периметр.
8 : 2 = 4 (см) – ширина прямокутника.
Треба побудувати прямокутник довжиною 8 см і шириною 4 см.
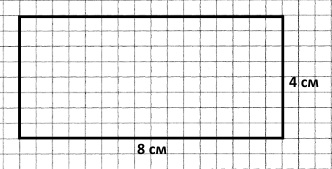
Р = 8 • 2 + 4 • 2 = 16 + 8 = 24 (см)
Відповідь: периметр прямокутника 24 сантиметри.
Завдання 192
За 2 год перший робітник обрізає 6 фруктових дерев, а другий — 4 дерева. За скільки годин ці робітники зможуть обрізати 15 дерев, якщо працюватимуть разом?
Короткий запис
І робітник — 6 дерев за 2 год
ІІ робітник — 4 дерева за 2 год
Разом — 15 дерев за ? год
Схема
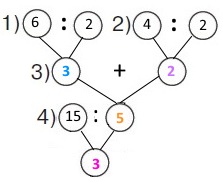
Вираз 15 : (6 : 2 + 4 : 2)
Розв’язання
1) 6 : 2 = 3 (д.) – І робітник за 1 год;
2) 4 : 2 = 2 (д.) – ІІ робітник за 1 год;
3) 3 + 2 = 5 (д.) – обрізають разом за 1 год;
4) 15 : 5 = 3 (год)
Відповідь: зможуть обрізати за 3 години.
Завдання 193 Ділення перевірили множенням
|
_627 | 3 6 209 _27 27 0 |
х 209 3 627 |
_972 | 9 9 108 _72 72 0 |
х 108 9 972 |
_872 | 4 8 218 _7 4 _32 32 0 |
х 218 4 872 |
_384 | 8 32 48 _64 64 0 |
х 48 8 384 |
Завдання 194 Зменшили у 10 разів (поділили на число 10):
200 : 10 = 20 20 : 10 = 2 220 : 10 = 22 1000 : 10 = 100 990 : 10 = 99 500 : 10 = 50 340 : 10 = 34
Завдання 195 Ділення з остачею
|
72 : 10 = 7 (ост. 2) |
255 : 10 = 25 (ост. 5) |
720 : 100 = 7 (ост. 20) |
355 : 100 = 3 (ост. 55) |
427 : 10 = 42 (ост. 7) |
Завдання 196
Якщо b = 108, c = 801, d = 9, тоді (с – b) : d = (801 – 108) : 9 = 693 : 9 = 77
Якщо b = 108, c = 801, d = 9, тоді b + (с : d) = 108 + (801 : 9) = 108 + 89 = 197
Якщо b = 108, c = 801, d = 9, тоді (b + с) : d = (108 + 801) : 9 = 909 : 9 = 101
Завдання 197 Порядок дій
|
272 – 40 + 96 : 8 = 272 – 40 + 12 = 232 + 12 = 244 |
(272 – 40 + 96) : 8 = (232 + 96) : 8 = 328 : 8 = 41 |
|
272 – (40 + 96) : 8 = 272 – 136 : 8 = 272 – 17 = 255 |
272 – (40 + 96 : 8) = 272 – (40 + 12) = 272 – 52 = 220 |
Завдання 198
1) Складена задача на знаходження суми числа і частки
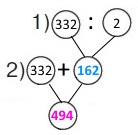
З поля в овочесховище привезли 332 ц цибулі, а капусти — удвічі менше. Скільки всього центнерів цибулі й капусти привезли в овочесховище?
Короткий запис
Цибуля — 332 кг
Капуста — ?, у 2 рази менше
Всього — ?
Схема
|
|
|
Вираз 332 + 332 : 2
|
Короткий запис №1 Цибуля — 332 кг Капуста — ?, у 2 рази менше |
Короткий запис Цибуля — 332 кг Капуста — 162 кг Всього — ?
|
План розв’язування
1) Скільки центнерів капусти привезли в овочесховище?
2) Скільки всього центнерів цибулі й капусти привезли в овочесховище?
Розв’язання
1) 332 : 2 = (200 + 120 + 12) : 2 = 162 (ц) – привезли капусти;
2) 332 + 162 = 494 (ц) – всього центнерів цибулі й капусти привезли.
Відповідь: в овочесховище привезли 494 центнери цибулі й капусти.
2) Складена задача на ділення на вміщення частки на число
З поля привезли 336 ц моркви, а буряків — у 4 рази менше. Усі буряки розфасували в контейнери, по 2 ц в кожний. Скільки контейнерів знадобилося?
Короткий запис
Моркви — 336 ц
Буряків — ?, у 4 рази менше — ? к. по 2 ц
Схема
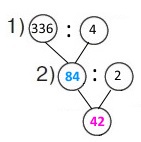
Вираз (332 : 4) : 2
|
Короткий запис №1 Морква — 336 ц Буряки — ?, у 4 рази менше |
Короткий запис №2 84 ц — це ? контейнерів по 2 ц Контейнери — ? к., 84 ц уміщає по 2 ц |
План розв’язування
1) Скільки привезли буряків?
2) Скільки контейнерів знадобилося?
Розв’язання
1) 336 : 4 = (320 + 16) : 4 = 80 + 4 = 84 (ц) – привезли буряків;
2) 84 : 2 = (80 + 4) : 2 = 42 (к.) – контейнерів знадобилося.
Відповідь: знадобилося 42 контейнери.
Завдання 199
1) Складена задача на знаходження суми числа і частки
На центральній площі міста висадили 186 кущів троянд, а в парку — утричі менше. Скільки всього кущів троянд висадили в парку й на площі?
Короткий запис
Площа — 186 кущів
Парк — ?, у 3 рази менше
Всього — ? кущів
Розв’язання
Вираз 186 + 186 : 3
1) 186 : 3 = (180 + 6) : 3 = 62 (к.) – кущів висадили в парку;
2) 186 + 62 = 186 + 14 + 48 = 248 (к.)
Відповідь: у парку й на площі висадили 248 кущів троянд.
Обернена задача на знаходження числа 3.
Висадили 248 кущів троянд, з них на центральній площі висадили 186 кущів троянд, а в парку решту. У скільки разів менше кущів висадили в парку, ніж на площі?
Короткий запис
Площа — ? кущів
Парк — 62 кущі, у ? разів менше
Всього — 248 кущів
Розв’язання
Вираз (248 – 62) : 62
1) 248 – 62 = 148 + (100 – 62) = 148 + 38 = 186 (к.) – кущів висадили на центральній площі;
2) 186 : 62 = 3 (рази)
Відповідь: у 3 рази більше висадили кущів на центральній площі, ніж у парку.
Завдання 200 Задача на зведення до одиниці
На пошиття шести костюмів на швейній фабриці витрачають 18 м тканини. Скільки таких костюмів можна пошити із 324 м тканини?
Короткий запис
6 костюмів — 18 м
? костюмів — 324 м
Схема
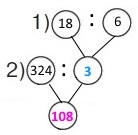
Вираз 324 : (18 : 6)
Розв’язання
1) 18 : 6 = 3 (м) – тканини витрачають на костюм;
2) 324 : 3 = (300 + 24) : 3 = 108 (к.) – костюмів можна пошити.
Відповідь: можна пошити 108 костюмів.
2) Змінили число в запитанні так, щоб у відповіді одержати число 150.
Скільки таких костюмів можна пошити із 450 м тканини?
Завдання 201 Поставте за даними діаграми ще кілька запитань.
1) Який динозавр мав найбільшу масу?
Брахіозавр (50 т)
2) Хто з динозаврів мав меншу масу, ніж апатозавр (25 т)?
Трицератопс (10 т), тиранозавр (15 т), спинозавр (5 т).
3) На скільки тонн трицератопс легший, ніж брахіозавр?
50 – 10 = 40 (т)
4) Які динозаври легші від тиранозавра (15 т)?
Трицератопс (10 т), спинозавр (5 т).
5) Яка загальна маса усіх динозаврів? На скільки тонн трицератопс легший, ніж тиранозавр?
Завдання 202
1) Складена задача на знаходження суми числа і частки
У супермаркет привезли 522 л мінеральної води, а солодкої — у 6 разів менше. Скільки всього літрів води привезли в супермаркет?
Короткий запис
Мінеральна — 522 л
Солодка — ?, у 6 разів менше
Всього — ? л
Розв’язання
Вираз 522 + 522 : 6
1) 522 : 6 = (480 + 42) : 6 = 87 (л) – літрів солодкої води привезли;
2) 522 + 87 = 520 + 80 + 9 = 609 (л) – всього літрів води привезли.
Відповідь: у супермаркет привезли 609 літрів води.
Обернена задача на знаходження числа 3.
У супермаркет привезли 522 л мінеральної води, а решту солодкої. У скільки разів менше привезли солодкої води, ніж мінеральної, якщо разом було 609 літрів?
Короткий запис
Мінеральна — ? л
Солодка — 87 л, у ? разів менше
Всього — 609 л
Розв’язання
Вираз (609 – 87) : 87
1) 609 – 87 = 609 – 100 + 13 = 509 + 13 = 522 (к.) – літрів мінеральної води привезли;
2) 522 : 87 = 6 (разів)
Відповідь: у 6 разів більше привезли мінеральної води, ніж солодкої.
Завдання 203
Суму чисел 145 і 78 збільшити втричі.
(145 + 78) • 3 = 223 • 3 = 669
Від числа 900 відняти частку чисел 972 і 9.
900 – (972 : 9) = 900 – 108 = 792
Добуток чисел 234 і 4 зменшити втричі.
234 • 4 : 3 = 936 : 3 = (300 + 30 + 6) : 3 = 312