|
а |
9 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
Дільники а |
1,3,9 |
1,2,3,4 6,12 |
1,13 |
1,2,7,14 |
1,3,5,15 |
1,2,4, 8,16 |
1,17 |
1,2,3,6,9,18 |
1,19 |
|
Просте |
– |
– |
+ |
– |
– |
– |
+ |
– |
+ |
|
Складене |
+ | + | – | + | + | + | – | + | – |
Вправа 3 Порядок дій
(68 • 12 – 45 • 13 + 42) : 21 = 13 — просте число
1) 68 • 12 = 816
2) 45 • 13 = 585
3) 816 – 585 = 231
4) 231 + 42 = 273
4) 273 : 21 = 13
Вправа 5 Ознаки подільності чисел
Числа, які діляться на 3 і менші за 20: 3, 6, 9, 12, 15, 18
Вправа 6
1) п'ять учнів мають вдома тварину кожного виду.
2) Кількість яких тварин ділиться на:
а) 2; 40, 10, 20
б) 3; 15, 45
в) 5; 5, 15, 45
г) 9; 45
ґ) 10? 10, 40, 20
3) Так, кількість власників кроликів є складеним числом.
4) Кількість власників собак і кішок разом: 40 + 45 + 20 = 105
Число 105 ділиться на: а) 2; Ні; б) 5; Так; в) 10? Ні.
5) Порівняй кількість власників хом’яків, рибок та кроликів разом із кількістю власників собак.
5 + 10 + 15 = 30, 45 + 20 = 65, 65 – 30 = 35
6) Опитали 15 + 40 + 45 + 10 + 5 + 20 + 20 = 155 дітей
7) Розклали на прості множники число власників:
а) кроликів; 15 = 3 • 5
б) котів; 40 = 2 • 2 • 2 • 5
в) собак. 65 = 5 • 13
Вправа 7
Остання цифра числа 234, що прикрита карткою:
|
а) 2, 4, 6, 8 |
б) 5, 0 |
в) 0 |
г) 3, 6, 9 |
ґ) 9 |
Вправа 8
а) парне чотирицифрове число: 3650
б) трицифрове число, що ділиться на 3: 603
в) трицифрове число, що ділиться на 10: 560
г) двоцифрове число, що ділиться на 9: 36
ґ) двоцифрове число, що ділиться на 5: 35
Вправа 9
Який номер шафи у спортклубі, якщо це найменше трицифрове число, яке ділиться на 9? 108
Вправа 10
Мені менше 15 років і мій вік ділиться на 12. Скільки мені років?
Вправа 11
|
а) 6 – 5х = 13 Помилкова умова |
б) 26 + (57 – 2х) = 59
83 – 2х = 59
2х = 83 – 59
2х = 24
х = 24 : 2
х = 12
Дільники числа 12: 1, 2, 3, 4, 6, 12
|
ГЕОМЕТРИЧНІ ФІГУРИ. ОБЧИСЛЕННЯ ПЛОЩ ТА ОБ’ЄМІВ ФІГУР
Вправа 2
|
Розгорнутий кут |
Прямий кут
|
Тупий кут
|
Вправа 4
|
∠А |
∠В |
∠С |
|
30° |
70° |
130° |
|
110° |
50° |
20° |
|
40° |
60° | 30° |
Вправа 5
Ширина екрана планшета дорівнює 22 см, що у 2 рази менше за довжину. Знайди площу екрана планшета та периметр рамки, що його обрамляє.
Розв'язання
1) 22 • 2 = 44 (см) – довжина екрана;
2) 22 • 44 = 968 (см²) – площа екрана;
3) (22 + 44) • 2 = 132 (см) – периметр рамки.
Відповідь: 968 см²; 132 см.
Вправа 6
Знайди площу і периметр кожного многокутника, якщо виміри подано в дециметрах.
Розв'язання
1) 3 • 3 = 9 (дм²) ‒ площа квадрата;
2) 3 • 4 = 12 (дм) ‒ периметр квадрата;
3) 3 • 4 : 2 = 6 (дм²) ‒ площа трикутника;
4) 3 + 4 + 5 = 12 (дм) - периметр трикутника;
5) 2 • 7 = 14 (дм²) ‒ площа прямокутника;
6) (2 + 7) • 2 = 18 (дм) ‒ периметр прямокутника.
Вправа 7
Знайди невідомі довжини сторін зображених многокутників, якщо периметр кожного дорівнює 24 см і виміри подано в сантиметрах.
Розв'язання
1) 24 - (6 + 5 + 2 + 8) = 3 (см)
2) 24 - (7 + 5 + 4) = 8 (см)
3) 24 - (1 + 7 + 2 + 3 + 6) = 5 (см)
Відповідь: 3 см; 8 см; 5 см.
Вправа 8
Виміри прямокутного паралелепіпеда 20 см, 15 см і 12 см. Знайди його об’єм, суму довжин усіх ребер та площу поверхні.
Розв'язання
1) 20 • 15 • 12 = 3600 (см3) ‒ об'єм паралелепіпеда;
2) 4 • (20 + 15 + 12) = 4 • 47 = 188 (см) ‒ сума довжин усіх ребер паралелепіпеда;
3) 2 • (20 • 15 + 20 • 12 + 15 • 12) = 2 • (300 + 240 + 180) = 2 • 720 = 1440 (дм²) ‒ площа поверхні паралелепіпеда.
Відповідь: 3600 см3; 188 см; 1440 см².
Вправа 9
Обчисли площу поверхні, суму довжин усіх ребер та об’єм куба, ребро якого дорівнює 2 м.
Розв'язання
1) 23 = 2 • 2 • 2 = 8 (м3) ‒ об'єм куба;
2) 12 • 2 = 24 (м) ‒ сума довжин усіх ребер куба;
3) 6 • 22 = 6 • 4 = 24 (м²) ‒ площа поверхні куба.
Відповідь: 8 м3; 24 м; 24 м².
Вправа 10
Задай значення для а, b і с так, щоб а було парним, b ділилось на 3, а c ділилось на 9. Знайди об’єм, площу поверхні та довжину всіх ребер прямокутного паралелепіпеда.
Дано: а = 4 см; b = 6 см; с = 9 см
Розв'язання
1) 4 • 6 • 9 = 216 (см3) ‒ об'єм паралелепіпеда;
2) 4 • (4 + 6 + 9) = 4 • 19 = 76 (см) ‒ сума довжин усіх ребер паралелепіпеда;
3) 2 • (4 • 6 + 4 • 9 + 6 • 9) = 2 • (24 + 36 + 54) = 2 • 114 = 228 (дм²) ‒ площа поверхні паралелепіпеда.
Відповідь: 216 см3; 76 см; 228 см².
Вправа 11
Об’єм ящика 18 дм3. Знайди висоту ящика, якщо його ширина 2,4 дм, а довжина на 6 см більша за ширину.
Розв'язання
1) 2,4 + 0,6 = 3 (дм) ‒ довжина ящика;
2) 2,4 • 3 = 7,2 (дм²) ‒ площа дна ящика;
3) 18 : 7,2 = 2,5 (дм) ‒ висота ящика.
Відповідь: 2,5 дм.
Вправа 12
Поверхня кожної піраміди має трикутників: 6; 3; 4; 5
В основі кожної піраміди многокутники: шестикутник, трикутник, чотирикутник, п'ятикутник.
Вправа 13
Об’ємні фігури: п'ятикутна призма; восьмикутна призма; шестикутна призма.
Відповідність між ними та їх розгортками: 1 — С; 2 — А, 3 — В
ПАРАЛЕЛЬНІ ТА ПЕРПЕНДИКУЛЯРНІ ПРЯМІ
Вправа 1
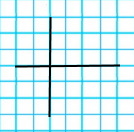
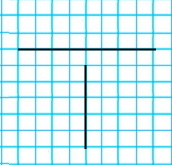
Паралельні прямі і перпендикулярні прямі.
Вправа 2
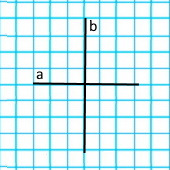
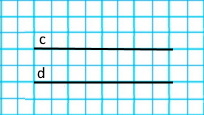
Дві чорні прямі є паралельними.
Вправа 3
 |
 |
 |
 |
Вправа 6
Паралельні відрізки: AB i CD i KL; RT i PS
Перпендикулярні відрізки: AB i RT; CD i RT, CD i PS
Вправа 7
|
|
 |
 |
Вправа 8
АВСDKPTM — прямокутний паралелепіпед.
|
а) КР і РВ — перпендикулярні
б) АК і РВ — паралельні
в) АВ і ВС — перпендикулярні
|
г) ВС і AD — паралельні
ґ) AB і CD — паралельні
д) AB і AD — перпендикулярні
|
Вправа 9
Пізанська вежа нахилена на 4⁰ від вертикального положення. Який кут нахилу вежі до землі?
Розв'язання
90⁰ – 4⁰ = 86⁰ – кут нахилу вежі до землі.
Відповідь: 86⁰.
Вправа 10
За таблицею побудуй лінійну діаграму кількості балів у щоденнику кожного з учнів. Проводимо два перпендикулярні промені зі спільним початком. Кількості 1 бал відповідає лінія, довжина якої дорівнює 1 клітинці зошита (5 мм), тому маємо на горизонтальному промені шкалу 0, 1, 2, ..., 12. Розмістимо на вертикальному промені через рівні відрізки шість точок і підписуємо під ними імена дітей. Довжина лінії Валентина становитиме 5 клітинок; Марини — 8, Поліни — 12, Дмитра — 3, Германа — 5, Орисі — 10. Самостійно зроби завдання.
ЗВИЧАЙНІ ДРОБИ. МІШАНІ ЧИСЛА. ПОРІВНЯННЯ. ДОДАВАННЯ І ВІДНІМАННЯ
Вправа 1 Ознайомлення з дробами
|
Площа початкового прямокутника |
18 од в. |
12 од. в. |
24 од. в. |
12 од.в. |
|
Площа зафарбованого прямокутника |
6 од. в. |
3 од. в. |
18 од. в. |
6 од в. |
|
Зафарбована частина |
1/3 |
1/4 |
3/4 |
1/2 |
Вправа 2 Одиниці вимірювання.
|
а) 30/100 м = 30 см
580/100 км = 500 м
540/1000 = 540 мм
|
2/10 дм = 2 см
34/100 м = 34 см
320/1000 кг = 320 г
|
165/1000 т = 165 кг
300/1000 кг = 300 г
430/1000 л = 430 мл
|
Вправа 3
Неправильні дроби: 1, 5/2, 9/5, 11/11, 24/5, 63/18
Мішані дроби: 5/2 = 2 1/2, 9/5 = 1 4/5, 24/5 = 4 4/5
Скоротні дроби: 63/18 = 7/9
Вправа 4
|
a) 2/6 < 4/6
|
б) 5/16 > 4/16
|
Вправа 5
|
3/5 < 4/5
3/4 > 2/4
|
5/8 < 7/8
10/10 > 9/10
|
2/3 < 1
6/6 = 1
|
5/6 < 1
7/7 = 1
|
Вправа 6
У порядку спадання: 6/7, 5/7, 2/7, 1/7
У порядку спадання: 13/13, 9/13, 6/13, 5/13
У порядку спадання: 1 5/19, 5/19, 1/19
Вправа 7
Морква — 1/2 кг, помідор — 5/4 кг, капуста — 3/4 кг, баклажан — 1/4 кг, картопля — 3/2 кг
У порядку зростання: 1/4, 3/4, 1/2, 5/4, 3/2
Вправа 8
4/10 + 6/10 = 10/10 — зафарбовано весь прямокутник
5/10 + 2/10 = 7/10 — зафарбовано 7 клітинок прямокутника.
Вправа 9
1/4 кг + 3/4 кг = 4/4 кг = 1 кг
8/1000 т + 1/1000 т = 9/1000 т = 9 кг
1 2/8 м + 6/8 м = 16/8 м = 2 м
3/10 л – 1/10 л = 2/10 л
2 1/4 ц + 2/4 ц = 11/4 ц = 2 3/4 ц
15/10 грн – 1/10 грн = 14/10 грн = 1 4/10 грн
Вправа 10
|
а) х – 3/12 = 11/12
х = 11/12 + 3/12
х = 14/12
х = 1 2/12
х = 1 1/6
|
б) 1 5/12 + х = 3 7/12
х = 3 7/12 – 1 5/12
х = 2 2/12
х = 2 1/6
|
в) 5 3/7 – х = 1 1/7
х = 5 3/7 – 1 1/7
х = 4 2/7
|
Вправа 11
Маса одного пакунка становить 2 2/5 кг, а другого — на 1 1/5 кг менше. Яка маса двох пакунків?
Розв'язання
1) 2 2/5 ‒ 1 1/5 = 1 1/5 (кг) ‒ маса другого пакунка;
2) 2 2/5 + 1 1/5 = 3 3/5 (кг) ‒ маса двох пакунків.
Відповідь: 3 3/5 кг.
Вправа 12
Сторони прямокутника дорівнюють 2 1/5 і 3 2/5 м. Знайди його периметр.
Розв'язання
(2 1/5 + 3 2/5) • 2 = 5 3/5 • 2 = 28/5 • 2 = 56/5 (м) = 11 1/5 м ‒ периметр прямокутника.
Відповідь: 11 1/5 м.
Вправа 13
До магазину завезли 5/23 т винограду, а персиків — на 2/23 т більше. До обіду продали 8/23 т завезених фруктів. Скільки фруктів ще залишилося у магазині?
Розв'язання
1) 5/23 + 2/23 = 7/23 (т) ‒ персиків завезли;
2) 7/23 + 2/23 = 12/23 (т) ‒ всього фруктів завезли;
3) 12/23 ‒ 8/23 = 4/23 (кг) ‒ фруктів залишилося.
Відповідь: 4/23 кг.
Вправа 14
За перший день туристи пройшли на байдарках 4/15 , а за другий день — 3/15 всього маршруту. Яку частину маршруту їм ще потрібно пройти?
Розв'язання
1) 4/15 + 3/15 = 7/15 (ч.) ‒ пройшли;
2) 1 ‒ 7/15 = 3/15 (ч.) = 1/5 (ч.) ‒ залишилося пройти.
Відповідь: 1/5 кг.