Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 7 Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої.
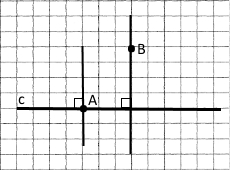
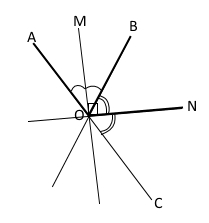
Завдання 138 На малюнках 7.7 – 7.10 зображено перпендикулярні прямі.
Перпендикулярні прямі перетинаються під прямим кутом.
7.7
7.10
Завдання 139 Накресліть пряму c та позначте точку A, що їй належить, і точку B, що їй не належить. Проведіть за допомогою косинця прямі через точки A і B так, щоб вони були перпендикулярними до прямої c.
Перпендикулярні прямі перетинаються під прямим кутом (90°).
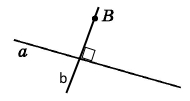
Завдання 140 Побудова перпендикулярних прямих
За допомогою косинця проведіть пряму b, що проходить через точку B перпендикулярно до прямої a.
Перпендикулярні прямі перетинаються під прямим кутом (90°).
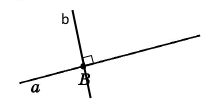
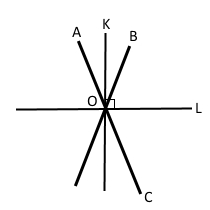
Завдання 141 На малюнку 7.13 прямі a і b перпендикулярні.
1) Відрізок АВ лежить на прямій а. Відрізок MN лежить на прямій b. Отже, відрізки AB і MN є перпендикулярними, бо лежать на перпендикулярних прямих а і b.
2) Промінь ЕА лежить на прямій а. Відрізок СМ лежить на прямій b. Отже, промінь EA і відрізок CM перпендикулярні, бо лежать на перпендикулярних прямих а і b.
3) Відрізки АВ і DE лежать на прямій а. Отже, відрізки AB і DE не є перпендикулярними, бо не лежать на перпендикулярних прямих.
4) Промінь CN лежить на прямій b. Відрізок СЕ лежить на прямій а. Отже промені CN і CE є перпендикулярними, бо лежать на перпендикулярних прямих а і b.
Завдання 142 На малюнку 7.13 прямі а і b перпендикулярні.
1) Відрізок DE лежить на прямій а. Відрізок CN лежить на прямій b. Отже, відрізки DE і CN є перпендикулярними, бо лежать на перпендикулярних прямих а і b.
2) Промінь CM лежить на прямій b. Промінь СА лежить на прямій а. Отже, промені СМ і СА перпендикулярні, бо лежать на перпендикулярних прямих а і b.
3) Промінь СЕ і відрізок СА лежать на прямій а. Отже, промінь СЕ і відрізок СА не є перпендикулярними, бо не лежать на перпендикулярних прямих.
4) Відрізок BD лежить на прямій a. Відрізок MN лежить на прямій b. Отже відрізки BD і MN є перпендикулярними, бо лежать на перпендикулярних прямих а і b.
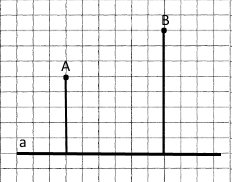
Завдання 143 Накресліть пряму а, позначте точку A, що розміщена на відстані 2,5 см від прямої а, та точку B, що розміщена на відстані 4 см від прямої а.
Відстань від точки до прямої – довжина відрізка, від точки А до точки перетину проведеного перпендикуляра з прямою.
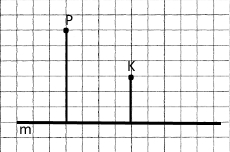
Завдання 144 Проведіть пряму m, позначте точку P, що розміщена на відстані 3 см від прямої m, та точку K, що розміщена на відстані 1,5 см від прямої m.
Відстань від точки до прямої – довжина відрізка, від точки А до точки перетину проведеного перпендикуляра з прямою.
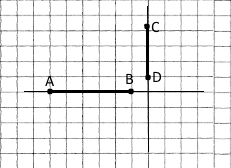
Завдання 145 Накресліть відрізки AB і CD так, щоб вони були перпендикулярними та не перетиналися.
Відрізки мають лежати на перпендикулярних прямих, але не перетинатися.
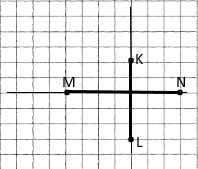
Завдання 146 Накресліть промені MN і KL так, щоб вони були перпендикулярними та перетиналися.
Відрізки мають лежати на перпендикулярних прямих і перетинатися.
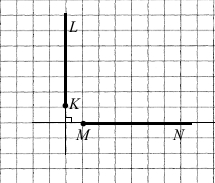
Завдання 147 (малюнок 7.14)
1) Прямі AB, KL і MN перетинаються в точці O. Чи є перпендикулярними прямі AB і MN, якщо ∠AOK = 25°, ∠KON = 66°?
Треба довести, що прямі АB і MN перетинаються під прямим кутом, тобто ∠AON = 90°.
Доведення.
Якщо промінь ОK проходить між сторонами кута AON, тоді справедлива основна властивість вимірювання кутів: ∠AON = ∠AOK + ∠KON.
∠AON = 25° + 66° = 91°. Отже, прямі АВ і MN не є перпендикулярними.
Відповідь: ні.
2) Прямі AB, KL і MN перетинаються в точці O. Чи є перпендикулярними прямі AB і MN, якщо ∠LON = 118, ∠LOB = 28°?
Треба довести, що прямі АB і MN перетинаються під прямим кутом, тобто ∠BON = 90°.
Доведення.
Якщо промінь ОB проходить між сторонами кута LON, тоді справедлива основна властивість вимірювання кутів: ∠LON = ∠LOB + ∠BON, тоді ∠BON = ∠LON – ∠LOB = 118° – 28° = 90°. Отже, прямі АВ і MN є перпендикулярними.
Відповідь: так.
Завдання 148 (малюнок 7.14)
1) Прямі AB, KL і MN перетинаються в точці O. Чи є перпендикулярними прямі AB і MN, якщо ∠MOK = 122°, ∠AOK = 31°?
Треба довести, що прямі АB і MN перетинаються під прямим кутом, тобто ∠МOА = 90°.
Дано прямі AB, KL, MN, які перетинаються в точці О.
Доведення.
Якщо промінь ОА проходить між сторонами кута МOК, тоді справедлива основна властивість вимірювання кутів: ∠МOК = ∠МOА + ∠АOК, тоді
∠МOА = ∠МOК – ∠АOК = 122° – 31° = 91°. Отже, прямі АВ і MN не є перпендикулярними.
Відповідь: ні.
2) Прямі AB, KL і MN перетинаються в точці O. Чи є перпендикулярними прямі AB і MN, якщо ∠MOL = 59°, ∠LOB = 31°?
Треба довести, що прямі АB і MN перетинаються під прямим кутом, тобто ∠AOВ = 90°.
Дано прямі AB, KL, MN, які перетинаються в точці О.
Доведення.
Якщо промінь ОL проходить між сторонами кута MOB, тоді справедлива основна властивість вимірювання кутів: ∠MOB = ∠MOL + ∠LOB.
∠MOB = 59° + 31° = 90°. Отже, прямі АВ і MN є перпендикулярними.
Відповідь: так.
Завдання 149 Чи є правильним означення: «Перпендикуляр до прямої – це будь-який відрізок, перпендикулярний до даної прямої»? Чому?
Неправильне означення, бо перпендикуляр до прямої – це відрізок, перпендикулярний до даної прямої, причому один з його кінців має належати цій прямій.
Завдання 150 (малюнок 7.15)
1) Прямі AB, CD і MN перетинаються в точці O, причому AB ⊥ CD. Знайдіть ∠MOD, якщо ∠NOB = 25°.
Якщо AB ⊥ CD, це означає, що прямі перетинаються під прямим кутом, тоді ∠AOD = 90°.
Якщо промінь ОМ проходить між сторонами кута AOD, тоді справедлива рівність
∠AOD = ∠AOM + ∠MOD.
Прямі АВ і MN, що перетинаються в точці О, утворюють пари вертикальних кутів. Вертикальні кути рівні: ∠AOM = ∠NOB.
∠MOD = ∠AOD – ∠AOM = ∠AOD – ∠NOB = 90° – 25° = 65°.
Відповідь: ∠MOD = 65°.
2) Прямі AB, CD і MN перетинаються в точці O, причому AB ⊥ CD. Знайдіть ∠CON, якщо ∠MOB = 150°.
Якщо AB + CD, це означає, що прямі перетинаються під прямим кутом, тоді ∠DOB = 90°.
Якщо промінь ОD проходить між сторонами кута MOB, тоді справедлива рівність
∠MOB = ∠MOD + ∠DOB, ∠MOD = ∠MOB – ∠DOB.
Прямі АВ і MN, що перетинаються в точці О, утворюють пари вертикальних кутів. Вертикальні кути рівні: ∠MOD = ∠CON.
∠MOD = ∠CON = ∠MOB – ∠DOB = 150° – 90° = 60°.
Відповідь: ∠CON = 60°.
Завдання 151 (малюнок 7.16)
1) Прямі KL, MN і PF перетинаються в точці O, причому KL ⊥ MN. Знайдіть ∠KOP, якщо ∠NOF = 140°.
Якщо KL ⊥ MN, це означає, що прямі перетинаються під прямим кутом, тоді ∠NOL = 90°.
Якщо промінь ОL проходить між сторонами кута NOF, тоді справедлива основна властивість вимірювання кутів ∠NOF = ∠NOL + ∠LOF, ∠LOF = ∠NOF – ∠LOF.
Прямі KL і MN, що перетинаються в точці О, утворюють пари вертикальних кутів. Вертикальні кути рівні: ∠KOP = ∠LOF.
∠LOF = ∠KOP = ∠NOF – ∠LOF = 140° – 90° = 50°.
Відповідь: ∠LOF = 50°.
2) Прямі KL, MN і PF перетинаються в точці O, причому KL ⊥ MN. Знайдіть ∠KOF, якщо ∠PON = 37°.
Якщо KL ⊥ MN, це означає, що прямі перетинаються під прямим кутом, тоді ∠KOM = 90°.
Якщо промінь ОM проходить між сторонами кута KOF, тоді справедлива основна властивість вимірювання кутів ∠KOF = ∠KOM + ∠MOF.
Прямі KL і MN, що перетинаються в точці О, утворюють пари вертикальних кутів. Вертикальні кути рівні: ∠PON = ∠MOF.
∠KOF = ∠KOM + ∠PON = 90° + 37° = 127°.
Відповідь: ∠KOF = 127°.
Завдання 152 Кути прямі ABC і CBM прямі. Доведіть, що точки A, B і M лежать на одній прямій.
Можна довести, що промені ВА і ВМ є доповняльними, тоді точки належать одній прямій.
Дано прямі кути АВС і СВМ.
Доведення.
Оскільки кути АВС і СВМ прямі, тоді ∠АВС = ∠СВМ = 90°. Точка С – є вершиною обох кутів, а точка В належить сторонам обох кутів. Оскільки градусні величини кутів однакові, а кути є різними, тоді вони лежать по різні сторони від променя ВС. Якщо промінь ВС проходить між сторонами ВА і ВМ, тоді за основною властивістю вимірювання кутів справедлива рівність ∠АВМ = ∠АВС + ∠СВМ = 90° + 90° = 180°. Кути АВС і СВМ – суміжні, вони утворюють розгорнутий кут, а їхні сторони є доповняльними променями, які доповнюють один одного до прямої.
Отже, АВ і ВМ є доповняльними променями, тому точки А, В, М лежать на одній прямій.
Завдання 153 Два суміжних кути, що утворилися в результаті перетину двох прямих, рівні між собою. Доведіть, що це перпендикулярні прямі.
Треба довести, що кут між цими прямими дорівнює 90°.
Дано два суміжні промені при перетині двох прямих.
Доведення.
Оскільки прямі, що перетинаються у спільній точці, ділять площину на дві пари вертикальних кутів. Вертикальні кути різних пар є суміжними, вони утворюють розгорнутий кут. Якщо кути рівні, тоді вони прямі, бо 180° : 2 = 90°. Оскільки кут не перевищує 90°, то він є шуканим кутом між прямими.
Отже, прямі перетинаються під прямим кутом, значить вони перпендикулярні.
Завдання 154 На малюнку 7.17 прямі AB ⊥ CD, ∠EON = 110°. Знайдіть ∠CON, якщо ∠AOE = 20°.
Якщо АВ ⊥ CD, це означає, що прямі перетинаються під прямим кутом, тоді ∠AOD = ∠DOB = ∠BOC = 90°, тоді ∠AOC = 90° • 3 = 270°.
Якщо промінь ОЕ і ON проходять таким чином між сторонами кута АOС, тоді за основною властивістю вимірювання кутів справедлива рівність ∠АОС = ∠AOE + ∠EON + ∠NOC, ∠AOC = ∠AOE + ∠EON + ∠CON.
Якщо рівні ліві частини рівності, тоді рівні її праві частини, маємо
∠AOE + ∠EON + ∠CON = 270°
∠CON = 270° – ∠AOE – ∠EON = 270° – 20° – 110° = 140°.
Відповідь: ∠CON = 140°.
Завдання 155 На малюнку 7.17 прямі AB ⊥ CD, ∠CON = 135°, ∠AOE = 25°. Знайдіть ∠EON.
Якщо АВ ⊥ CD, це означає, що прямі перетинаються під прямим кутом, тоді ∠AOD = ∠DOB = ∠BOC = 90°, тоді ∠AOC = 90° • 3 = 270°.
Якщо промінь ОЕ і ON проходять таким чином між сторонами кута АOС, тоді за основною властивістю вимірювання кутів справедлива рівність ∠АОС = ∠AOE + ∠EON + ∠NOC, ∠AOC = ∠AOE + ∠EON + ∠CON.
Якщо рівні ліві частини рівності, тоді рівні її праві частини, маємо
∠AOE + ∠EON + ∠CON = 270°
∠EON = 270° – ∠AOE – ∠CON = 270° – 25° – 135° = 110°.
Відповідь: ∠EON = 110°.
Завдання 156 На малюнку 7.18 ∠AOB = ∠COD, ∠BOC = ∠DOE. Доведіть, що OC ⊥ AE і BO ⊥ OD.
Щоб довести, що OC ⊥ AE, треба довести, що ∠АОС = 90°.
Доведення.
Промені ОА і ОЕ мають спільний початок і доповнюють пряму, тоді вони доповняльні і утворюють розгорнутий кут ∠АОЕ = 180°.
За основною властивістю вимірювання відрізків ∠АОЕ = ∠АОВ + ∠ВОС + ∠COD + ∠DOE.
Оскільки ∠AOB = ∠COD, ∠BOC = ∠DOE, тоді ∠АОЕ = ∠АОВ + ∠ВОС + ∠АОВ + ∠ВОС,
∠АОЕ = 2 (∠АОВ + ∠ВОС), ∠АОЕ = 2 ∠АОС, ∠АОС = ∠АОЕ : 2 = 180° : 2 = 90°.
Отже, OC ⊥ AE.
Щоб довести, що ВО ⊥ OD, треба довести, що ∠BOD = 90°.
Доведення.
Промені ОА і ОЕ мають спільний початок і доповнюють пряму, тоді вони доповняльні і утворюють розгорнутий кут ∠АОЕ = 180°.
За основною властивістю вимірювання відрізків ∠АОЕ = ∠АОВ + ∠ВОС + ∠COD + ∠DOE.
Оскільки ∠AOB = ∠COD, ∠BOC = ∠DOE, тоді ∠АОЕ = ∠COD + ∠ВОС + ∠COD + ∠ВОС,
∠АОЕ = 2 (∠BOC + ∠COD), ∠АОЕ = 2 ∠BOD, ∠BOD = ∠АОЕ : 2 = 180° : 2 = 90°.
Отже, BO ⊥ OD.
Завдання 157 Доведіть, що промінь, проведений через вершину кута перпендикулярно до його бісектриси, є бісектрисою кута, суміжного з даним.
Треба довести, що кути АОВ і ВОС є суміжними, тобто мають спільну сторону, а інші дві сторони є доповняльними променями – утворюють розгорнутий кут ∠AOC = 180°.
Дана бісектриса кута ОМ, перпендикулярний до неї промінь ОN.
Доведення.
Кути АОВ і ВОС мають спільну вершину О і сторону ОВ.
Якщо промінь ОМ є бісектрисою кута АОВ, він ділить його на два рівні кути ∠АОМ = ∠МОВ.
Якщо промінь ОN є бісектрисою кута BОC, він ділить його на два рівні кути ∠BОN = ∠NОC.
Якщо промінь ОВ проходить між сторонами кута MON, тоді за основною властивістю вимірювання кутів ∠MON = ∠MOB + ∠BON.
Якщо промінь ОN, проведений через вершину кути перпендикулярно до бісектриси ОМ, тоді ON ⊥ OM, вони утворюють прямий кут ∠MON = 90°.
Якщо промені ОК, ОM, ОB, ON проходять між сторонами кута АОС, тоді за основною властивістю вимірювання кутів ∠AOC = ∠AOM + ∠MOB + ∠BON + ∠NOC.
∠AOC = ∠MOB + ∠MOB + ∠BON + ∠BON
∠АОС = 2 (∠MOB + ∠BON)
∠АОС = 2 ∠MON = 2 • 90° = 180°.
Промені OА і ОС є доповняльними, тому АОВ і ВОС – суміжні.
Завдання 158 Промені OK і OL є бісектрисами кутів AOB і BOC відповідно, причому OK ⊥ OL. Доведіть, що кути AOB і BOC – суміжні.
Треба довести, що кути АОВ і ВОС мають спільну сторону, а інші дві сторони є доповняльними променями, тобто утворюють розгорнутий кут ∠AOC = 180°.
Дано бісектриси OK і OL відповідно кутів AOB і BOC, причому OK ⊥ OL.
Доведення.
Кути АОВ і ВОС мають спільну вершину О і сторону ОВ.
Якщо промінь ОВ проходить між сторонами кута KOL, тоді за основною властивістю вимірювання кутів ∠KOL = ∠KOB + ∠BOL.
Якщо промені OK ⊥ OL, тоді вони перетинаються в точці О та утворюють прямий кут ∠KOL = 90°.
Промінь ОК є бісектрисою кута АОВ, він ділить його на два рівні кути ∠АОК = ∠КОВ.
Промінь ОL є бісектрисою кута ВОС, він ділить його на два рівні кути ∠BOL = ∠LOC.
Якщо промені ОК, ОВ, ОL проходять між сторонами кута АОС, тоді за основною властивістю вимірювання кутів
∠AOC = ∠AOK + ∠KOB + ∠BOL + ∠LOC.
∠AOC = ∠KOB + ∠KOB + ∠BOL + ∠BOL
∠АОС = 2 (∠KOB + ∠BOL)
∠АОС = 2 ∠KOL = 2 • 90° = 180°.
Промені OА і ОС є доповняльними, тому АОВ і ВОС – суміжні.
Завдання 159
1) На прямій послідовно позначено точки M, N і K. Знайдіть MK, якщо MN = 3 см 2 мм, NK = 4,1 см = 4 см 1 мм.
Якщо на прямій послідовно позначено точки M, N і K, тоді за основною властивістю вимірювання відрізків MK = MN + NK = 3 см 2 мм + 4 см 1 мм = 7 см 3 мм
Відповідь: МК = 7 см 3 мм.
2) На прямій послідовно позначено точки M, N і K. Знайдіть MN, якщо MK = 7,8 см, NK = 2 см 5 мм = 2,5 см.
Якщо на прямій послідовно позначено точки M, N і K, тоді за основною властивістю вимірювання відрізків MK = MN + NK = 7,8 см + 2,5 см = 10,3 см
Відповідь: МК = 10,3 см.
Завдання 160 Знайдіть суміжні кути, різниця яких дорівнює 36°.
Суміжні кути утворюють розгорнутий кут, який дорівнює 180°.
Якщо різниця суміжних кутів дорівнює 36°, тоді знаємо, що один із них на стільки більший від іншого.
Нехай х (°) – менший кут, тоді х + 36 (°) – більший кут. Складемо рівняння.
х + х + 36 = 180
2х = 180 – 36
2х = 144
х = 144 : 2
х = 72 (°) – менший кут.
х + 36 = 72 + 36 = 108 (°) – більший кут.
Відповідь: суміжні кути 72° і 108°.
Життєва математика
Завдання 161 Рулон шпалер має 50 см завширшки і 10 м завдовжки. Потрібно обклеїти стіни в кімнаті, довжина якої 4,5 м, ширина – 3 м, а висота – 2,5 м. Загальна площа вікна і дверей становить 3,5 м2.
1) Скільки рулонів потрібно купити?
Розв’язання
50 см = (50 : 100) м = 0,05 м
1) 0,05 • 10 = 0,5 (м2) – площа шпалер у одному рулоні.
2) (4,5 • 2,5) • 2 + (3 • 2,5) • 2 = 22,5 + 15 = 37,5 (м2) – сума площ бокових граней.
3) 37,5 – 3,5 = 34 (м2) – площа стін для обклеювання.
Короткий запис
1 рулон — 0,5 м2
? рулонів — 34 м2
4) 34 : 0,5 = 68 (р.) – рулонів потрібно купити.
Відповідь: треба купити 68 рулонів шпалер.
2) Скільки коробок клею знадобиться, якщо для того, щоб поклеїти 4 рулони шпалер, витрачається одна коробка?
Короткий запис
1 коробка — 4 рулони
? коробок — 68 рулонів
Розв’язання
1) 68 : 4 = 17 (к.) – коробок клею знадобиться.
Відповідь: 17 коробок клею.
3) Скільки коштуватимуть матеріали, якщо рулон шпалер коштує 240 грн, а коробка клею – 85 грн?
Короткий запис
Шпалери — ? грн, 68 рулонів по 240 грн
Клей — ? грн, 17 коробок по 85 грн
Всього — ?
Розв’язання
1) 240 • 68 = 16320 (грн) – вартість шпалер.
2) 17 • 85 = 1445 (грн) – вартість клею.
3) 1620 + 1445 = 3065 (грн) – коштуватимуть матеріали.
Відповідь: матеріали коштуватимуть 3 065 гривень.
Підготуйтеся до вивчення нового матеріалу
Завдання 162
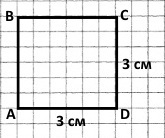
Дві пари паралельних прямих (не перетинаються): АВ і CD BC і AD.
Завдання 163 Периметр прямокутника дорівнює 32 см, а довжина кожної з його сторін є цілим числом сантиметрів.
32 : 2 = 16 (см) – півпериметр (сума довжини і ширини прямокутника).
Тоді сторони і площі можуть приймати наступні значення.
|
16 = 1 + 15 16 = 2 + 14 16 = 3 + 13 16 = 4 + 12 |
S = 1 • 15 = 15 (см2) S = 2 • 14 = 28 (см2) S = 3 • 13 = 39 (см2) S = 4 • 12 = 48 (см2) |
16 = 5 + 11 16 = 6 + 10 16 = 7 + 9 16 = 8 + 8 |
S = 5 • 11 = 55 (см2) S = 6 • 10 = 60 (см2) S = 7 • 9 = 56 (см2) S = 8 • 8 = 64 (см2) |
1) Чи може площа прямокутника дорівнювати 256 см2? Ні.
2) Чи може площа прямокутника дорівнювати 220 см2? Ні.
3) Чи може площа прямокутника дорівнювати 64 см2? Так.
4) Чи може площа прямокутника дорівнювати 60 см2? Так.
5) Чи може площа прямокутника дорівнювати 55 см2? Так.
6) Чи може площа прямокутника дорівнювати 54 см2? Ні.