Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 16 Третя ознака рівності трикутників
Завдання 399
На малюнку 16.5 трикутники є рівними між собою за третьою ознакою рівності трикутників (за рівністю відповідних сторін).
Завдання 400 Малюнок 16.6
Доведіть рівність трикутників ABC і CDA, AB = DC і BC = AD.
За умовою AB = DC і BC = AD, АС – спільна сторона трикутників ABC і CDA. Отже, за третьою ознакою рівності трикутників ∆ABC = ∆CDA.
Завдання 401 Малюнок 16.7
Доведіть, що ∆ACD = ∆ABD, якщо AC = AB і DC = DB.
За умовою сторони трикутників AC = AB і DC = DB, AD – спільна сторона трикутників ACD і ABD. Отже, за третьою ознакою рівності трикутників ∆ACD = ∆ABD.
Завдання 402 Малюнок 16.8
Сторони трикутників MK = ML, KN = NL. Доведіть, що ∠K = ∠L.
За умовою сторони трикутників MK = ML, KN = NL, MN – спільна сторона трикутників MKN і MLN. За третьою ознакою рівності трикутників ∆MKN = ∆MLN. Отже, відповідні кути ∠K = ∠L.
Завдання 403 Малюнок 16.9
Сторони трикутників PK = ML, PM = KL. Доведіть, що ∠PKM = ∠LMK.
За умовою сторони трикутників PK = ML, PM = KL, КM – спільна сторона трикутників KPM і MLK. За третьою ознакою рівності трикутників ∆KРМ = ∆MLК. Отже, відповідні кути ∠PKM = ∠LMK.
Завдання 404 Малюнок 16.10
Сторони трикутників AB = BC, AK = KC. Доведіть, що BK – бісектриса кута ABC.
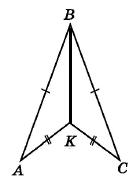
За умовою сторони трикутників AB = BC, AK = KC. Сполучимо відрізком точки В і К, отримаємо ВК – спільну сторону трикутників АВК і СВК. За третьою ознакою рівності трикутників ∆АВС = ∆СВК, тоді ∠АВК = ∠СВК, або ∠АВС = 2∠АВК. Отже, ВК – бісектриса кута АВС.
Завдання 405 Малюнок 16.11
Сторони трикутників MP = MK, PL = KL. Доведіть, що ML – бісектриса кута PMK.
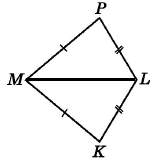
За умовою сторони трикутників MP = MK, PL = KL. Сполучимо відрізком точки M і L, отримаємо ML – спільну сторону трикутників MPL і MKL. За третьою ознакою рівності трикутників ∆MPL = ∆MKL, тоді ∠PML = ∠KML, або ∠PMK = 2∠PML. Отже, ML – бісектриса кута PMK.
Завдання 406 Малюнок 16.12
Дано: AB = CD, AC = BD. Довести: ∆AOD – рівнобедрений.
За умовою сторони трикутників AB = CD, AC = BD. Відрізок DA – спільна сторона трикутників ACD і DBA. За третьою ознакою рівності трикутників ∆ACD = ∆DBA, тому = ∠ADB = ∠DAO. За ознакою рівнобедреного трикутника (якщо два кути рівні, тоді трикутник рівнобедрений) ∆AOD – рівнобедрений.
Завдання 407 Малюнок 16.13
Дано: AO = OB, CO = OD. Довести: ∆ABC = ∆BAD.
За умовою сторони трикутників AO = OB, CO = OD. Вертикальні кути ∠DOB = ∠COA. За першою ознакою рівності трикутників (двома сторонами і кутом між ними) ∆DOB = ∆COA, тому CA = DВ. За основною властивістю вимірювання відрізків DA = AO + OD, CB = CO + OB = OB + CO = AO + OD, якщо рівні праві частини рівності, тоді рівні ліві частини, тому DA = CB. Сторона АВ – спільна для трикутників ABC і BAD. Отже, за третьою ознакою рівності трикутників ∆ABC = ∆BAD.
Завдання 408
Про трикутники ABC і MNP відомо, що AB ≠ MN, BC ≠ NP, AC ≠ MP. Чи можуть бути рівними такі трикутники.
Для рівних трикутників порядок запису вершин встановлюється рівністю відповідних кутів цих трикутників. Отримуємо відповідні сторони, які рівні. Тому для рівних трикутників АВС і MNP маємо мати відповідні сторони AB = MN, BC = NP, AC = MP, що суперечить умові. Отже, такі трикутники не можуть бути рівними.
Завдання 409
Трикутники ABC і MNP – рівнобедрені. Відомо, що AB = MN = 6 см, а BC = NP = 8 см. Чи можна стверджувати, що ці трикутники рівні?
Для рівних трикутників маємо мати відповідні сторони АВ = MN = 6 см, ВС = NP = 8 см, АС = МР. Наприклад, для рівнобедреного трикутника АВС, у якого АВ = 6 см, ВС = 8 см, АС – інша бічна сторона, нехай АС = 8 см. Для рівнобедреного трикутника MNP, у якого MN = 6 см, NP = 8 см, MP – інша бічна сторона, нехай МР = 6 см. Для таких трикутників не буде виконуватися третя ознака рівності трикутників, отже, не можна стверджувати, що трикутники рівні.
Завдання 410
Усередині рівнобедреного трикутника ABC (AB = AC) взято точку K так, що BK = KC. Доведіть, що пряма AK перпендикулярна до BC.
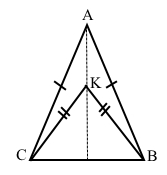
За умовою у рівнобедреному трикутнику АВС бічні сторони АВ = АС, тоді ВС – основа. Сполучимо точки А і К. За умовою ВК = КС, АВ = АС. Відрізок АК – спільна сторона трикутників ВАК і САК. За третьою ознакою рівності трикутників ∆ВАК = ∆САК, звідси ∠ВАК = ∠САК. Відрізок АК лежить на бісектрисі кута А до основи рівнобедреного трикутника АВС. Оскільки бісектриса рівнобедреного трикутника є висотою, то відрізок АК лежить на висоті, проведеній до основи ВС, такі відрізки перпендикулярні АК ﬩ ВС. За означенням перпендикулярні відрізки лежать на перпендикулярних прямих. Отже, пряма АК перпендикулярна до ВС.
Завдання 411
Усередині рівнобедреного трикутника DMN (DM = DN) взято точку P так, що MP = PN. Доведіть, що пряма DP ділить навпіл сторону MN.
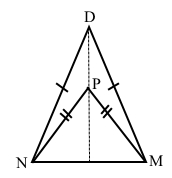
За умовою у рівнобедреному трикутнику DMN бічні сторони DM = DN, тоді MN – основа. Сполучимо точки D і P. За умовою MP = PN, DM = DN. Відрізок DP – спільна сторона трикутників MDP і NDP. За третьою ознакою рівності трикутників ∆MDP = ∆NDP, звідси ∠MDP = ∠NDP. Відрізок DP лежить на бісектрисі кута D до основи рівнобедреного трикутника DMN. Оскільки бісектриса рівнобедреного трикутника є медіаною, то відрізок DP лежить на медіані, проведеній до основи MN. Медіана в точці перетину ділить основу MN рівнобедреного трикутника навпіл. Отже, пряма DP, на якій лежить відрізок DP, ділить навпіл сторону MN.
Вправи для повторення
Завдання 412
Використовуючи шаблон кута, градусна міра якого 10°, побудувати перпендикулярні прямі.
10° • 9 = 90°
Наприклад, провести горизонтальну пряму. Послідовно відкласти 9 разів кути по 10°. Провести вертикальну пряму. Утворені прямі перпендикулярні, оскільки між прямими кут прямий.
Завдання 413
Промінь AK проходить між сторонами кута BAC, ∠BAC = 126°. Відомо, що 4∠BAK = 5∠KAC. Знайдіть градусні міри кутів BAK і KAC.
За основною властивістю вимірювання кутів ∠ВАС = ∠ВАК + ∠КАС. ∠ВАК : ∠КАС = 5 : 4.
Нехай х(°) – градусна міра частини, тоді 5х (°) – величина кута ВАК, 4х (°) – величина кута КАС. Складемо рівняння.
5х + 4х = 126
9х = 126
х = 126 : 9
х = (90 + 36) : 9
х = 14 (°) – 1 частина.
14 • 5 = 70 (°) – кут ВАК.
14 • 4 = 56 (°) – кут КАС.
Відповідь: ∠ВАК = 70°, ∠КАС = 56°.
Завдання 414
Інженери полюбляють трикутник за жорсткість форми: якщо сторони, що утворюють його, з'єднати у вершинах, то форму трикутника неможливо змінити, на відміну від інших геометричних фігур. Властивість жорсткості трикутника широко використовують на практиці. Так, Щоб закріпити стовп у вертикальному положенні, до нього ставлять підпорку.
Інші приклади використання цієї властивості: трикутники використовують у підйомних кранах, заводських конструкціях, різних архітектурних спорудах, ажурні металоконструкції основані на трикутниках, рівнобедрені трикутники слугують підтримкою для опор мостів, високовольтні опори мають у формі набір трикутників, урізана засувка замка, консервний ніж, домкрат.
Завдання 415
Накресліть трикутники ABC та KLM. Знайдіть суму кутів кожного трикутника.
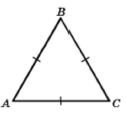
60° + 60° + 60° = 180°
Сума кутів трикутника дорівнює 180°.
Завдання 416
Накресліть прямокутник розміром 4 х 6 клітинок. Покажіть, як «замостити» (покрити без накладань і вільних клітинок) його куточками, кожний з яких складається з трьох клітинок, так, щоб жодні два з них не утворювали прямокутника.
