Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 18 Зовнішній кут трикутника та його властивості, співвідношення між сторонами і кутами трикутника
Завдання 463
Кут ∠1 є зовнішнім кутом трикутника ABC на малюнку 18.6.
Завдання 464
Накресліть ∆ABC та його зовнішній кут при вершині A.
Зовнішній кут при вершині А – це суміжний для кута А.
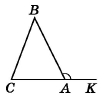
Завдання 465
Накресліть ∆DMN та його зовнішній кут при вершині D.
Зовнішній кут при вершині D – це суміжний для кута D.
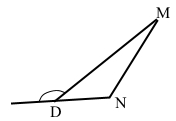
Завдання 466
Укажіть суму внутрішнього кута трикутника і його зовнішнього кута при тій самій вершині.
Внутрішній кут трикутника і його зовнішній кут при тій самій вершині є суміжними. За теоремою про суміжні кути їхня сума дорівнює 180°.
Відповідь: 180°.
Завдання 467 Малюнок 18.6
Зовнішній кут при вершині C трикутника ABC дорівнює 65° Знайдіть суму внутрішніх кутів A і B цього трикутника.
За властивістю зовнішнього кута трикутника ∠А + ∠В = 65°.
Відповідь: 65°.
Завдання 468 Малюнок 18.6
Сума внутрішніх кутів A і B трикутника ABC дорівнює 70°. Знайдіть зовнішній кут цього трикутника при вершині C.
За теоремою про властивість зовнішнього кута трикутника маємо градусну міру зовнішнього кута при вершині С, що дорівнює ∠А + ∠В = 70°.
Відповідь: 70°.
Завдання 469 Малюнок 18.7
У ∆PLK PL < LK. Порівняйте кути P і K цього трикутника.
Проти сторони PL лежить кут К, проти сторони LK – кут Р. За умовою LК > РL, тоді згідно теореми про співвідношення між сторонами і кутами трикутника (проти більшої сторони лежить більший кут) ∠Р > ∠К.
Відповідь: ∠Р > ∠К.
Завдання 470 Малюнок 18.7
У ∆PLK ∠L > ∠K. Порівняйте сторони PK і PL цього трикутника.
Проти кута L лежить сторона PK, проти кута К – сторона PL. За умовою ∠L > ∠K, тоді згідно теореми про співвідношення між сторонами і кутами трикутника (проти більшого кута лежить більша сторона) РК > РL.
Відповідь: РК > РL.
Завдання 471 Малюнок 18.7
Два кути трикутника дорівнюють 62° і 37°. Знайдіть градусну міру зовнішнього кута при третій вершині.
За теоремою про властивість зовнішнього кута трикутника маємо градусну міру зовнішнього кута при третій вершині, що дорівнює 62° + 37° = 99°.
Відповідь: 99°.
Завдання 472
У трикутнику ABC ∠A = 43°, ∠B = 102°. Знайдіть градусну міру зовнішнього кута при вершині С.
За теоремою про властивість зовнішнього кута трикутника маємо градусну міру зовнішнього кута при вершині С, що дорівнює ∠А + ∠В = 43° + 102° = 145°.
Відповідь: 145°.
Завдання 473
Скільки гострих кутів може бути серед зовнішніх кутів трикутника?
Зовнішній кут трикутника при вершині – це його суміжний кут.
За наслідком про суміжний кут – суміжним до гострого кута є тупий, і навпаки.
У тупокутного трикутника згідно наслідку теореми про суму кутів трикутника один кут тупий кут і два інші - гострі, тому такий трикутник має один гострий і два тупих зовнішніх кути.
У гострокутному трикутнику всі кути гострі, а суміжні до них кути – тупі, тому нема жодного гострого зовнішнього кута.
У прямокутному трикутнику один кут прямий, інші два гострі, такий трикутник має один прямий і два тупі зовнішні кути.
Відповідь: 1 гострий кут або жодного.
Завдання 474
Зовнішній кут при вершині рівнобедреного трикутника дорівнює 100°. Знайдіть кут при основі трикутника.
За властивістю зовнішнього кута трикутника маємо суму кутів при основі. За властивістю рівнобедреного трикутника кути при основі рівні, тому 100° : 2° = 50° – кут при основі трикутника.
Відповідь: 50°.
Завдання 475
Кут при основі рівнобедреного трикутника дорівнює 55°. Знайдіть зовнішній кут при вершині кута між бічними сторонами.
За властивістю рівнобедреного трикутника кути при основі рівні, тому знайдемо їхню суму 55° + 55° = 110°. Зовнішній кут при вершині дорівнює знайденій сумі (за властивістю зовнішнього кута трикутника).
Відповідь: 110°.
Завдання 476
Зовнішній кут при вершині A трикутника ABC дорівнює 105°. Знайдіть ∠B, якщо ∠C = 45°.
За властивістю зовнішнього кута при вершині А маємо рівність ∠В + ∠С = 105°, тоді ∠В = 105° – ∠С = 105° – 45° = 60°.
Відповідь: 60°.
Завдання 477
Один із зовнішніх кутів трикутника дорівнює 120°. Знайдіть внутрішній кут трикутника, не суміжний з ним, якщо другий внутрішній кут трикутника, не суміжний з ним, дорівнює 18°.
Зовнішній кут трикутника дорівнює сумі кутів трикутника не суміжних із ним.
Нехай х (°) – внутрішній не суміжний до зовнішнього, за властивістю зовнішнього кута складемо рівняння.
х + 18 = 120
х = 120 – 18
х = 102 (°) – градусна міра шуканого внутрішнього кута.
2 спосіб
За теоремою про суму суміжних кутів знайдемо суміжний з поданим внутрішній кут трикутника 180° – 120° = 60°. За теоремою про суму кутів трикутника 180° – (60° + 18°) = 102° – шуканий внутрішній кут трикутника.
Відповідь: 102°.
Завдання 478
Внутрішні кути трикутника дорівнюють 45° і 70°. Знайдіть градусну міру зовнішніх кутів трикутника, взятих по одному при кожній з його вершин.
За теоремою про суму кутів трикутника 180° – (45° + 70°) = 65° – третій внутрішній кут трикутника.
Згідно властивості зовнішнього кута знайдемо зовнішні кути при кожній вершині трикутника.
70° + 65° = 135° – градусна міра зовнішнього кута при вершині 45°.
45° + 65° = 110° – градусна міра зовнішнього кута при вершині 70°.
45° + 70° = 115° – градусна міра зовнішнього кута при вершині 65°.
2 спосіб
За теоремою про суму кутів трикутника 180° – (45° + 70°) = 65° – третій внутрішній кут трикутника.
За означенням зовнішній кут – це суміжний до внутрішнього кута, тому зовнішні кути трикутника при кожній вершині можна шукати за теоремою про суміжні кути.
180° – 45 ° = 135° – градусна міра зовнішнього кута при вершині 45°.
180° – 70° = 110° – градусна міра зовнішнього кута при вершині 70°.
180° – 65° = 115° – градусна міра зовнішнього кута при вершині 65°.
Відповідь: 135°, 110°, 115°.
Примітка для перевірки: оскільки трикутник мав три гострі внутрішні кути, тому отримали три тупі зовнішні кути.
Завдання 479
Зовнішні кути при двох вершинах трикутника відповідно дорівнюють 110° і 140°. Знайдіть градусну міру кожного з трьох внутрішніх його кутів.
За означенням зовнішній кут – це суміжний до внутрішнього кута, тому внутрішні кути трикутника при кожній вершині можна шукати за теоремою про суміжні кути.
180° – 110° = 70° – градусна міра внутрішнього кута при вершині 110°.
180° – 140° = 40° – градусна міра внутрішнього кута при вершині 140°.
За теоремою про суму кутів трикутника 180° – (70° + 40°) = 70° – третій внутрішній кут трикутника.
Відповідь: 70°, 40°, 70°.
Примітка: отримали рівнобедрений трикутник (за ознакою рівнобедреного трикутника – якщо два кути рівні, тоді трикутник рівнобедрений).
Завдання 480
1) У трикутнику ABC зовнішній кут при вершині C дорівнює 140°. Знайдіть внутрішні кути A і B цього трикутника, якщо кут B на 30° більший за кут A.
Застосуємо теорему про зовнішній кут трикутника.
Нехай х (°) – ∠А, тоді х + 30 (°) – ∠В. Складемо рівняння.
х + х + 30 = 140
2х + 30 = 140
2х = 140 – 30
2х = 110
х = 110 : 2 = (100 + 10) : 2 = 55 (°) – ∠А.
х + 30 = 55 + 30 = 85 (°) – ∠В.
2) У трикутнику ABC зовнішній кут при вершині C дорівнює 140°. Знайдіть внутрішні кути A і B цього трикутника, якщо кут A у 4 рази більший за кут B.
Застосуємо теорему про зовнішній кут трикутника.
Нехай х (°) – ∠В, тоді 4х (°) – ∠А. Складемо рівняння.
4х + х = 140
5х = 140
х = 140 : 5 = (100 + 40) : 5 = 28 (°) – ∠В.
4х = 28 • 4 = (20 + 8) • 4 = 112 (°) – ∠А.
Назва одного із символів нашої держави:
|
28° |
55° |
85° |
28° |
112° |
55° |
|
П |
Р |
А |
П |
О |
Р |
Завдання 481
1) Один із зовнішніх кутів трикутника дорівнює 120°. Знайдіть внутрішні кути, які не суміжні з ним, якщо один з них на 20° менший від другого.
За теоремою про зовнішній кут трикутника від дорівнює сумі двох інших несуміжних з ним внутрішніх кутів.
Нехай х (°) – менший внутрішній несуміжний із заданим зовнішнім, тоді х + 20 (°) – більший внутрішній несуміжний із заданим зовнішнім. Складемо рівняння.
х + (х + 20) = 120
2х + 20 = 120
2х = 120 – 20
2х = 100
х = 100 : 2
х = 50 (°) – менший кут.
х + 20 = 50 + 20 = 70 (°) – більший кут.
Відповідь: 50°, 70°.
2) Один із зовнішніх кутів трикутника дорівнює 120°. Знайдіть внутрішні кути, які не суміжні з ним, якщо один з них утричі менший від другого.
За теоремою про зовнішній кут трикутника від дорівнює сумі двох інших несуміжних з ним внутрішніх кутів.
Нехай х (°) – менший внутрішній несуміжний із заданим зовнішнім, тоді 3х (°) – більший внутрішній несуміжний із заданим зовнішнім. Складемо рівняння.
х + 3х = 120
4х = 120
х = 120 : 4
х = 30 (°) – менший кут.
3х = 30 • 3 = 90 (°) – більший кут.
Відповідь: 30°, 90°.
Завдання 482
Один із зовнішніх кутів рівнобедреного трикутника дорівнює 118°. Знайдіть градусні міри внутрішніх кутів трикутника.
І випадок.
Нехай зовнішній кут до кута при вершині рівнобедреного трикутника дорівнює 118°. За теоремою про суміжні кути 180° – 118° = 62° – внутрішній кут при вершині. За теоремою про зовнішній кут трикутника сума його внутрішніх кутів при основі дорівнює 118°. За властивістю рівнобедреного трикутника кути при основі рівні, тому 118° : 2 = 59° – внутрішній кут при основі трикутника.
Відповідь: 59°, 59°, 62°.
ІІ випадок.
Нехай зовнішній кут до кута при основі рівнобедреного трикутника дорівнює 118°. За теоремою про суміжні кути 180° – 118° = 62° – внутрішній кут при основі. За теоремою про зовнішній кут трикутника сума внутрішнього кута при основі та при вершині дорівнює 118°. За властивістю рівнобедреного трикутника його кути при основі рівні, тому 118° – 62 = 56° – внутрішній кут при вершині трикутника.
Відповідь: 62°, 62°, 56°.
Скільки розв'язків має задача?
Якщо дано зовнішній тупий кут, за наслідком з теореми про суму суміжних кутів внутрішній кут при цій вершині гострий. За наслідком з теореми про суму кутів трикутника щонайбільше може бути три гострі кути. За властивістю рівнобедреного трикутника кути при основі рівні, тому маємо 2 випадки, або 6 розв'язків.
Завдання 483
Один із зовнішніх кутів рівнобедреного трикутника дорівнює 42°. Знайдіть градусні міри внутрішніх кутів трикутника.
Нехай зовнішній кут до кута при вершині рівнобедреного трикутника дорівнює 42°. За теоремою про суміжні кути 180° – 42° = 138° – внутрішній кут при вершині. За теоремою про зовнішній кут трикутника сума його внутрішніх кутів при основі дорівнює 42°. За властивістю рівнобедреного трикутника кути при основі рівні, тому 42° : 2 = 21° – внутрішній кут при основі трикутника.
Відповідь: 21°, 21°, 138°.
Скільки розв'язків має задача?
Якщо дано зовнішній гострий кут, за наслідком з теореми про суму суміжних кутів внутрішній кут при цій вершині тупий. За наслідком з теореми про суму кутів трикутника може бути тільки один тупий кут. За властивістю рівнобедреного трикутника кути при основі рівні, тому маємо 1 випадок, або 3 розв'язки.
Завдання 484
Доведіть, що сума зовнішніх кутів будь-якого трикутника, взятих по одному при кожній вершині, дорівнює 360°.
Дано трикутник АВС. За теоремою про зовнішній кут трикутника можна записати ∠В + ∠С – суміжний кут для внутрішнього кута трикутника при вершині А, ∠А + ∠С – суміжний кут для внутрішнього кута трикутника при вершині В, ∠А + ∠В – суміжний кут для внутрішнього кута трикутника при вершині С.
Знайдемо їхню суму (∠В + ∠С) + (∠А + ∠С) + (∠А + ∠В) = 2 • (∠А + ∠В + ∠С). За теоремою про суму кутів трикутника ∠А + ∠В + ∠С = 180°. Отже, (∠В + ∠С) + (∠А + ∠С) + (∠А + ∠В) = 2 • 180° = 360°.
Завдання 485
Зовнішні кути трикутника відносяться як 3 : 5 : 4. Знайдіть відношення його внутрішніх кутів.
Сума зовнішніх кутів, взятих по одному при кожній вершині, дорівнює 360°.
1) 3 + 5 + 4 = 12 (ч.) – частин припадає на 360°.
2) 12 : 2 = 6 (ч.) – припадає на 180°.
Внутрішній кут при вершині є суміжним до зовнішнього кута.
6 – 3 = 3 (ч.) – внутрішній кут при вершині, де зовнішній становить 3 частини.
6 – 5 = 1 (ч.) – внутрішній кут при вершині, де зовнішній становить 5 частин.
6 – 4 = 2 (ч.) – внутрішній кут при вершині, де зовнішній становить 4 частини.
Складемо відношення 3 : 1 : 2.
2 спосіб
Нехай х (ч.) – внутрішній кут Х, у (ч.) – внутрішній кут У, z (ч.) – внутрішній кут Z. Згідно теореми про зовнішній кут трикутника складемо три рівняння (зовнішній кут трикутника дорівнює сумі внутрішніх кутів не суміжних із ним).
z + у = 3 (ч.) – частин припадає на зовнішній кут при вершині Х.
z + x = 5 (ч.) – частин припадає на зовнішній кут при вершині Y.
x + y = 4 (ч.) – частин припадає на зовнішній кут при вершині Z.
y = 3 – z
x = 5 – z
Підставимо у третє рівняння, отримаємо
(5 – z) + (3 – z) = 4
8 – 2z = 4
2z = 8 – 4
2z = 4
z = 4 : 2
z = 2
х = 5 – z = 5 – 2 = 3
y = 3 – 2 = 1
Складемо відношення z : х : у = 3 : 1 : 2.
Відповідь: 3 : 1 : 2.
Завдання 486
Внутрішні кути трикутника відносяться як 7 : 8 : 9. Знайдіть відношення зовнішніх кутів трикутника, не знаходячи їхніх градусних мір.
Сума кутів трикутника дорівнює 180°, також сума суміжних кутів дорівнює 180°.
7 + 8 + 9 = 24 (ч.) – припадає на суму кутів трикутника, або суму внутрішнього кута і суміжного до нього зовнішнього кута.
24 – 7 = 17 (ч.) – частин припадає на зовнішній кут до внутрішнього, який має 7 частин.
24 – 8 = 16 (ч.) – частин припадає на зовнішній кут до внутрішнього, який має 8 частин.
24 – 9 = 15 (ч.) – частин припадає на зовнішній кут до внутрішнього, який має 9 частин.
Складемо відношення відповідних зовнішніх кутів.
Відповідь: 17 : 16 : 15.
Завдання 487
Доведіть, що бісектриси зовнішнього і внутрішнього кутів трикутника при одній вершині перпендикулярні між собою.
Дано у трикутнику АВС промінь AD – бісектриса кута А, AF – бісектриса зовнішнього кута ВАК. Треба довести, що ∠DAЕ = 90°.
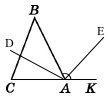
За умовою AD – бісектриса кута А, тому ∠САВ = 2∠DAB. За умовою AF – бісектриса кута ВАК, тому ∠ВАК = 2∠ВАЕ. За умовою кут ВАК – зовнішній для кута А (за означенням кут суміжний), тому ∠САК = ∠САВ + ∠ВАК = 180° (за теоремою про суміжні кути).
∠САК = 2∠DAB + 2∠BAE = 2 (∠DAB + ∠BAE) = 2∠DAE = 180°. Між бісектрисами AD і AE кут прямий: ∠DAE = 180° : 2 = 90°. Отже, бісектриси перпендикулярні.
Завдання 488
Промінь, що проходить між сторонами прямого кута, ділить його на два кути, різниця яких складає 1/3 від їх суми. Знайдіть градусні міри цих кутів.
За властивістю вимірювання кутів сума утворених кутів дорівнює даному прямому куту.
Величина різниці кутів показує на скільки один кут більший від другого.
Нехай х (°) – більший кут, тоді 90 – х (°) – менший кут. Складемо рівняння.
х – (90 – х) = 1/3 • 90
х – 90 + х = 30
2х = 30 + 90
2х = 120
х = 120 : 2
х = 60 (°) – більший кут.
90 – х = 90 – 60 = 30 (°) – менший кут.
2 спосіб
Нехай х (°) – менший кут, тоді 90 – х (°) – більший кут. Складемо рівняння.
90 – х – х = 1/3 • 90
90 – 2х = 30
2х = 90 – 30
2х = 60
х = 60 : 2
х = 30 (°) – менший кут.
90 – х = 90 – 30 = 60 (°) – більший кут.
3 спосіб
Нехай х (°) – менший кут. Складемо рівняння.
х + (х + 1/3 • 90) = 90
х + х + 30 = 90
2х + 30 = 90
2х = 90 – 30
2х = 60
х = 60 : 2
х = 30 (°) – менший кут.
х + 1/3 • 90 = 30 + 30 = 60 (°) – більший кут.
Відповідь: 30°, 60°.
Завдання 489
Відрізок AB, довжина якого 22,8 см, поділено на три частини. Відношення двох з них дорівнює 1 : 2, а третя – на 1,8 см довша за більшу з двох перших частин. Знайдіть довжини кожної з трьох частин відрізка.
Нехай х (см) – перша довжина (одна частина), тоді 2х (см) – друга довжина, 2х + 1,8 (см) – третя довжина. За властивістю вимірювання відрізків складемо рівняння.
х + 2х + 2х + 1,8 = 22,8
5х = 22,8 – 1,8
5х = 21
х = 21 : 5
х = 4,2 (см) – перша довжина.
2х = 4,2 • 2 = 8,4 (см) – друга довжина.
2х + 1,8 = 8,4 + 1,8 = 10,2 (см) – третя довжина.
Відповідь: 4,2 см, 8,4 см, 10,2 см.
Життєва математика
Завдання 490
У розпорядженні дитячого садочка є дві ділянки. Одна з них має форму прямокутника, 32 м завдовжки і 18 м завширшки. Друга ділянка є квадратною, такої самої площі, що й перша. У садівника є 97 м паркану.
1) Яку з ділянок садівник зможе обгородити парканом?
1) Р = (32 + 18) • 2 = 100 (м) – периметр прямокутної ділянки.
2) 97 < 100 Прямокутну ділянку не зможе обгородити.
3) S = 32 • 18 = 576 (м2) – площа квадратної ділянки (площа прямокутної ділянки).
4) 576 = 242, тому 24 м – сторона квадратної ділянки.
5) Р = 24 • 4 = (20 + 4) • 4 = 96 (м) – периметр квадратної ділянки.
Відповідь: зможе обгородити квадратну ділянку.
2) Скільки метрів паркану ще потрібно докупити, щоб можна було обгородити парканом обидві ділянки?
1) 100 + 96 = 196 (м) – сума всіх довжин для обгородження (сума периметрів).
2) 196 – 97 = 99 (м) – метрів паркану потрібно докупити.
Відповідь: потрібно докупити 99 метрів паркану.
Підготуйтеся до вивчення нового матеріалу
Завдання 491
Накресліть трикутник ABC, у якого ∠C = 90°, ∠A = 30°. У скільки разів сторона ВС цього трикутника менша від сторони АВ.
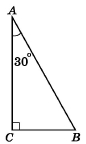
АВ = 2СВ
Відповідь: у 2 рази менша.
Завдання 492
Накресліть трикутник ABC, у якого ∠C = 90°, та проведіть медіану CM цього трикутника. У скільки разів медіана CM менша від сторони AB?
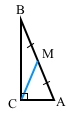
АВ = 2СМ
Відповідь: у 2 рази менша.
Завдання 493
Розріжте деякий квадрат на два рівних між собою п'ятикутники.