ГДЗ геометрія 7 клас домашня самостійна робота № 4 Істер

Інші завдання дивись тут...

Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."

(умови завдань з підручника подані чорним кольором)

Домашня самостійна робота № 4 (§§ 17-20)

Завдання 1 Три кути трикутника можуть дорівнювати...

Сума кутів трикутника дорівнює 180°, тому маємо трикутник з кутами 50° + 60° + 70° = 180°.

A 20°, 20° і 150° Б 30°, 100° і 40°

B 50°, 60° і 70° Г 60°, 60° і 61°

Завдання 2 У ∆ABC AB > AC. Порівняйте ∠B і ∠C цього трикутника.

Проти сторони АВ знаходиться ∠С, проти сторони АС знаходиться ∠В.

Проти більшої сторони лежить більший кут, тому ∠С > ∠В (тобто ∠В < ∠С)

A ∠B < ∠C Б ∠В = ∠C

B ∠В > ∠C Г порівняти неможливо

Завдання 3 Знайдіть другий гострий кут прямокутного трикутника, якщо перший дорівнює 40°.

Сума гострих кутів прямокутника дорівнює 90°, тому 90° – 40° = 50°.

А 30° Б 40° В 50° Г 60°

Завдання 4 Один з кутів трикутника дорівнює 72°. Знайдіть суму двох інших кутів трикутника.

Сума кутів трикутника дорівнює 180°, тому 180° – 72° = 108° – сума двох інших кутів.

А 98° Б 108° В 118° Г знайти неможливо

Завдання 5 Зовнішній кут при вершині рівнобедреного трикутника дорівнює 140°. Знайдіть кут при основі цього трикутника.

Зовнішній кут при вершині дорівнює сумі двох інших внутрішніх кутів не суміжних з ним (у нашому випадку сумі кутів при основі).

У рівнобедреному трикутнику кути при основі рівні, тому

140° : 2 = 70°

А 40° Б 50° В 60° Г 70°

Завдання 6 Дві сторони трикутника дорівнюють 2,7 см і 4,2 см. Якому цілому числу сантиметрів НЕ може дорівнювати третя сторона трикутника?

Нехай а – третя сторона трикутника.

Складемо нерівність трикутника.

4,2 – 2,7 < а < 4,2 + 2,7

1,5 < а < 6,9

Третя сторона може дорівнювати цілому числу 2, 3, 4, 5, 6.

Третя сторона НЕ може дорівнювати числу 8.

А 2 см Б 4 см В 6 см Г 8 см

Завдання 7 Один з гострих кутів прямокутного трикутника на 30° менший від другого, а гіпотенуза трикутника дорівнює 8 см. Знайдіть менший з його катетів.

^{Короткий запис}

^{І кут — ?}

^{ІІ кут — на 30° більше}

^{Всього — 90°}

Сума гострих кутів прямокутного трикутника дорівнює 90°

Нехай х (°) – один гострий кут, тоді х + 30 (°) – другий гострий кут. Складемо рівняння.

х + х + 30 = 90

2х + 30 = 90

2х = 90 – 30

2х = 60

х = 60 : 2

х = 30 (°) – один кут.

х + 30 = 30 + 30 = 60 (°) – другий кут.

Менший катет лежить проти меншого кута 30°. За властивістю катета проти кута 30° (дорівнює половині гіпотенузи) отримали менший із катетів 8 см : 2 = 4 см.

А 2 см Б 4 см В 5 см Г 6 см

Завдання 8 У трикутнику два кути дорівнюють 60° і 50°. Знайдіть кут між прямими, що містять бісектриси цих кутів.

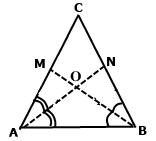
Нехай ∠A = 60°, AN – його бісектриса, тоді ∠NAB = 60° : 2 = 30°. За умовою ∠В = 50°, ВМ – його бісектриса, тоді ∠МВА = 50° : 2 = 25°. Оскільки О – точка перетину бісектрис, тоді справедлива рівність ∠NAB = ∠OAB = 30°, ∠MBA = ∠OBA = 25°.

У ∆АОВ два кути гострі, тоді третій тупий. Бісектриси AN і BM, що перетинаються в точці О, утворюють дві пари суміжних кутів, тому ∠NOВ – зовнішній кут до тупого кута, він буде гострим. За теоремою про зовнішній кут ∠NOВ = ∠OAB + ∠OBA = 30° + 25° = 55° – гострий кут між бісектрисами, він буде кутом між прямими, що містять бісектриси кутів.

2 спосіб

За теоремою про суму кутів ∆АОВ отримаємо ∠АОВ = 180° – ∠ОАВ – ∠ОВА = 180° – 25° – 30° = 125°.

Бісектриси AN і BM утворюють дві пари суміжних кутів при одній прямій, тому ∠NOВ = 180° – ∠АОВ = 180° – 125° = 55° – гострий кут між бісектрисами, він буде кутом між прямими, що містять бісектриси кутів.

А 125° Б 115° В 65° Г 55°

Завдання 9 Периметр трикутника дорівнює 16 см. Якою НЕ може бути довжина однієї з його сторін?

16 – 8 = 8 (см) – сума двох інших сторін. Сторона 8 см дорівнює сумі інших двох сторін, оскільки не виконується нерівність трикутника, вона не може бути стороною такого трикутника.

А 8 см Б 7,5 см В 7 см Г 2 см

Завдання 10 Бісектриса кута при основі рівнобедреного трикутника дорівнює основі цього трикутника. Знайдіть кут при основі цього трикутника.

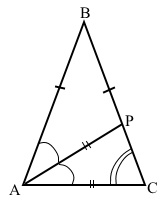
У рівнобедреного трикутника кути при основі рівні.

Нехай 2х (°) – ∠С при основі трикутника АВС, тоді х (°) – кут між бісектрисою і основою цього трикутника. За умовою бісектриса і основа рівні, маємо рівнобедрений ∆АРС, у якого ∠АРС = ∠С = 2х. Складемо рівняння за теоремою про суму кутів трикутника.

2х + х + 2х = 180

5х = 180

х = 180 : 5

х = (150 + 30) : 5

х = 36 (°) – кут між бісектрисою та основою.

2х = 36 • 2 = 72 (°) – ∠С при основі рівнобедреного трикутника.

А 60° Б 72° В 84° Г 96°

Завдання 11 Зовнішні кути трикутника відносяться як 3 : 5 : 7. Знайдіть менший з внутрішніх кутів трикутника.

Зовнішній кут трикутника суміжний до внутрішнього кута при одній вершині. Сума кутів трикутника дорівнює 180°.

Нехай х (°) – градусна міра частини зовнішнього кута, звідси 3х (°) – перший зовнішній кут, 5х (°) – другий зовнішній кут, 7х (°) – третій зовнішній кут, тоді 180 – 3х (°) – перший внутрішній кут, 180 – 5х (°) – другий внутрішній кут, 180 – 7х (°) – третій внутрішній кут. Складемо рівняння.

(180 – 3х) + (180 – 5х) + (180 – 7х) = 180

180 – 3х + 180 – 5х + 180 – 7х = 180

180 + 180 + 180 – 180 = 3х + 5х + 7х

360 = 15х

х = 360 : 15

х = 360 : 3 : 5

х = 24 (°) – одна частина.

Менший внутрішній кут буде суміжним до більшого зовнішнього кута.

180 – 7х = 180 – 7 • 24 = 12 (°) – менший внутрішній кут.

А 12° Б 24° В 60° Г інша відповідь

Завдання 12 У прямокутному трикутнику один з кутів дорівнює 60°, а сума меншого катета і медіани, проведеної до гіпотенузи, дорівнює 10 см. Знайдіть гіпотенузу трикутника.

За властивістю про гострі кути прямокутного трикутника 90° – 60° = 30° – інший гострий кут. Менша сторона лежить проти меншого кута.

Нехай х (см) – гіпотенуза, тоді х/2 (см) – менший катет (катет проти кута 30° дорівнює половині гіпотенузи), х/2 (см) – медіана (медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи). Складемо рівняння.

х/2 + х/2 = 10

2х/2 = 10

х = 10 (см) – гіпотенуза.

А 6 см Б 8 см В 10 см Г 15 см

Завдання 13 Установіть відповідність між кутами та їхніми градусними мірами.

У прямокутному трикутнику один з гострих кутів дорівнює 40°.

Нехай ∠С = 90°, ∠В = 40°.

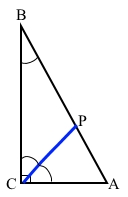
1) Кут, що утворює висота трикутника, проведена до гіпотенузи, із більшим катетом.

За властивістю гострих кутів прямокутного трикутника ∠А = 90° – ∠В = 90° – 40° = 50 (°) – інший гострий кут. Більший катет СВ лежить проти більшого гострого кута ∠А. Проведемо висоту СР до гіпотенузи, СР ﬩ АВ, ∠СРВ = 90°. Розглянемо ∆СРВ – прямокутний, ∠ВСР = 90° – ∠В = 90° – 40° = 50°.

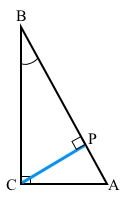
2) Менший з кутів, що утворює бісектриса прямого кута з гіпотенузою.

За властивістю гострих кутів прямокутного трикутника ∠А = 90° – ∠В = 90° – 40° = 50 (°) – інший гострий кут. Проведемо бісектрису СР до гіпотенузи АВ, ∠АСР = 1/2 ∠С = 90° : 2 = 45°. Розглянемо ∆АСР, за теоремою про суму кутів трикутника ∠АРС = 180° – ∠А – ∠АСР = 180° – 50° – 45° = 85° – шуканий менший з кутів.

3) Кут між прямими, що містять бісектриси прямого і меншого гострого кута трикутника.

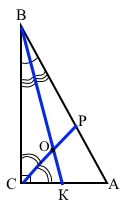
За властивістю гострих кутів прямокутного трикутника ∠А = 90° – ∠В = 90° – 40° = 50 (°) – більший гострий кут. Проведемо бісектрису СР до гіпотенузи АВ, ∠РСВ = 1/2 ∠С = 90° : 2 = 45°. Проведемо бісектрису кута ВK, ∠CВK = 1/2 ∠B = 40° : 2 = 20°. Для точки О, що є точкою перетину бісектрис справедливо ∠РСВ = ∠ОСВ = 45°, ∠NBC = ∠ОВС = 20°. Бісектриси ВК і СР лежать на прямих, які перетинаються, тому вони утворюють дві пари суміжних кутів. Кут між шуканими прямими – це зовнішній кут для внутрішнього кута ∠СОВ у ∆СОВ, за теоремою про зовнішній кут ∠РОВ = ∠ОСВ + ∠ОВС = 45° + 20° = 65°.

1. —> Б 50°

2. —> Г 85°

3. —> В 65°

Завдання для перевірки знань до §§ 17-20

Завдання 1 Знайдіть третій кут трикутника, якщо два з його кутів дорівнюють 30° і 80°.

За теоремою про суму кутів трикутника 180° – (80° + 30°) = 70° – третій кут трикутника.

Відповідь: 70°.

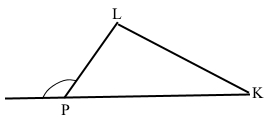
Завдання 2 Накресліть ∆PLK та його зовнішній кут при вершині P.

Завдання 3 За якими елементами рівні між собою прямокутні трикутники, зображені на малюнку? Запишіть відповідні рівності.

За умовою трикутники АВС і EDF – прямокутні, ∠А = ∠D = 90°, катети АС = DF = 3 см, прилеглі гострі кути до катетів ∠С = ∠F = 50°. Отже, ∆АВС = ∆DEF за катетом і прилеглим гострим кутом.

Завдання 4 Кут при основі рівнобедреного трикутника дорівнює 71°. Знайдіть кут при вершині цього трикутника.

У рівнобедреного трикутника кути при основі рівні. За теоремою про суму кутів трикутника 180° – (71° + 71°) = 38° – кут при вершині.

Відповідь: 38°.

Завдання 5 На малюнку BP – висота трикутника ABC до сторони АС, ∠ABP = 32°, ∠PBC = 67°. Знайдіть кути трикутника ABC.

За умовою ВР – висота трикутника АВС, РВ ﬩ АС, ∠АРВ = ∠СРВ = 90°.

Розглянемо ∆АВР – прямокутний. За властивістю гострих кутів прямокутного трикутника ∠А = 90° – ∠АВР = 90° – 32° = 58°.

Розглянемо ∆СВР – прямокутний. За властивістю гострих кутів прямокутного трикутника ∠С = 90° – ∠РВС = 90° – 67° = 23°.

Висота ВР проходить між сторонами кута В, тому за властивістю вимірювання кутів ∠В = ∠АВР + ∠РВС = 32° + 67° = 99°.

Відповідь: 23°, 58°, 99°.

Завдання 6 Дві сторони трикутника дорівнюють 5,2 см і 6,3 см. Якому найбільшому цілому числу сантиметрів може дорівнювати третя сторона?

Нехай а (см) – невідома третя сторона. Складемо нерівність трикутника.

6,3 – 5,2 < а < 6,3 + 5,2

1,1 < а < 11,5

Найбільше ціле число, що задовольняє нерівність – 11. Отже, третя сторона може дорівнювати 11 см.

Відповідь: 11 см.

Завдання 7 Один з кутів трикутника вдвічі менший від другого і на 16 ° більший за третій. Знайдіть кути трикутника.

^{Короткий запис}

^{І кут — ?}

^{ІІ кут — у 2 рази більший, ніж І}

^{ІІІ кут — на 16° менша, ніж І}

^{Всього — 180°}

Сума кутів трикутника дорівнює 180°.

Нехай х (°) – перший кут, тоді 2х (°) – другий кут, а х – 16 (°) – третій кут. Складемо рівняння.

х + 2х + (х – 16) = 180

х + 2х + х – 16 = 180

4х – 16 = 180

4х = 180 + 16

4х = 196

х = 196 : 4

х = (160 + 36) : 4

х = 49 (°) – перший кут.

2х = 49 • 2 = (40 + 9) • 2 = 98 (°) – другий кут.

х – 16 = 49 – 16 = 33 (°) – третій кут.

Відповідь: 49°, 98°, 33°.

Завдання 8 Один із зовнішніх кутів трикутника дорівнює 112°. Знайдіть внутрішні кути, не суміжні з ним, якщо вони відносяться як 3 : 5.

Зовнішній кут трикутника дорівнює сумі внутрішніх кутів, не суміжних із ним.

Нехай х (°) – градусна міра частини внутрішніх несуміжних кутів, тоді 3х (°) – один внутрішній несуміжний кут, 5х (°) – другий внутрішній несуміжний кут. Складемо рівняння за теоремою про зовнішній кут.

3х + 5х = 112

8х = 112

х = 112 : 8

х = (80 + 32) : 8

х = 14 (°) – одна частина.

3х = 14 • 3 = (10 + 4) • 3 = 42 (°) – один внутрішній несуміжний кут.

5х = 14 • 5 = (10 + 4) • 5 = 70 (°) – другий внутрішній несуміжний кут.

Відповідь: 42°, 70°.

Завдання 9 У прямокутному трикутнику BCD ∠C = 90°, BM – бісектриса трикутника, ∠CBD = 60°. Знайдіть довжину катета CD, якщо CM = 8 см.

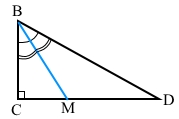
За умовою ∆ВСD – прямокутний, ∠C = 90°. За властивістю гострих кутів прямокутного трикутника ∠D = 90° – ∠CBD = 90° – 60° = 30°.

ВМ – бісектриса ∠CBD, тоді ∠СВМ = ∠МВD = ∠CBD : 2 = 60° : 2 = 30°.

У прямокутному ∆ВСМ гіпотенуза ВМ = 2СМ = 2 • 8 см = 16 см (катет СМ проти кута 30° дорівнює половині гіпотенузи ВМ).

∆BMD – рівнобедрений, оскільки ∠МВD = ∠D = 30° (ознака рівнобедреного трикутника за двома рівними кутами), тому за означенням такого трикутника ВМ = МD = 16 см.

Точка М належить катету CD, тому за властивістю вимірювання відрізків CD = CM + MD = 8 см + 16 см = 24 см.

Відповідь: 24 см.

Додаткові вправи

Завдання 10 Зовнішні кути трикутника відносяться як 4 : 5 : 6. Знайдіть відношення внутрішніх кутів трикутника.

Сума зовнішніх кутів, взятих по одному при кожній вершині, дорівнює 360°.

1) 4 + 5 + 6 = 15 (ч.) – частин припадає на 360°.

2) 15 : 2 = 15/2 (ч.) – припадає на 180°.

Внутрішній кут при вершині є суміжним до зовнішнього кута.

15/2 – 4 = 15/2 – 8/2 = 7/2 (ч.) – внутрішній кут при вершині, де зовнішній становить 4 частини.

15/2 – 5 = 15/2 – 10/2 = 5/2 (ч.) – внутрішній кут при вершині, де зовнішній становить 5 частин.

15/2 – 6 = 15/2 – 12/2 = 3/2 (ч.) – внутрішній кут при вершині, де зовнішній становить 6 частини.

Складемо відношення 7/2 : 5/2 : 3/2 .

2 спосіб

Нехай х (ч.) – внутрішній кут Х, у (ч.) – внутрішній кут У, z (ч.) – внутрішній кут Z. Згідно теореми про зовнішній кут трикутника складемо три рівняння (зовнішній кут при вершині трикутника дорівнює сумі внутрішніх несуміжних кутів).

z + у = 4 (ч.) – частин припадає на зовнішній кут при вершині Х.

z + x = 5 (ч.) – частин припадає на зовнішній кут при вершині У.

x + y = 6 (ч.) – частин припадає на зовнішній кут при вершині Z.

y = 4 – z

x = 5 – z

Підставимо у третє рівняння, отримаємо

(4 – z) + (5 – z) = 6

4 – z + 5 – z = 6

9 – 2z = 6

2z = 9 – 6

2z = 3

z = 3 : 2