ГДЗ геометрія 7 клас Істер дотична до кола, взаємне розміщення прямої і кола

Інші завдання дивись тут...

Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."

(умови завдань з підручника подані чорним кольором)

§ 22 Дотична до кола, її властивості, взаємне розміщення прямої і кола

Завдання 639

На малюнку 22.4 пряма m є дотичною.

На малюнку 22.4 пряма m є січною.

Завдання 640

1) Тільки одну дотичну можна провести до кола через точку, що лежить на колі.

^{Через дотичну і центр кола можна провести тільки одну пряму (радіус), дотична перпендикулярна до радіуса (якщо прямі перетинаються під прямим кутом, тоді всі інші кути перетину прямих також прямі), тому маємо тільки одну дотичну.}

2) Дві різних дотичних можна провести до кола через точку, що лежить поза колом.

^{Будемо мати дві дотичні і відповідно дві точки дотику.}

3) Жодної дотичної не можна провести до кола через точку, що лежить усередині кола.

^{Тоді пряма перетинатиме коло у двох точках, що суперечить визначенню дотичної.}

Завдання 641

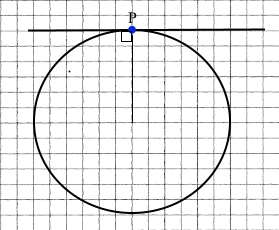
Накресліть коло, радіус якого дорівнює 3 см, позначте на ньому точку P. За допомогою косинця проведіть через точку P дотичну до цього кола.

Завдання 642

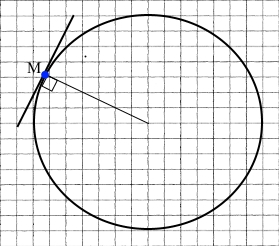
Накресліть коло, радіус якого дорівнює 3,5 см, позначте на ньому точку M. За допомогою косинця або транспортира проведіть дотичну через точку M до цього кола.

Завдання 643

Радіус кола дорівнює 6 см.

1) Якщо відстань від центра кола до прямої дорівнює 4 см, то пряма а і коло мають дві спільні точки (січна до кола).

2) Якщо відстань від центра кола до прямої дорівнює 6 см, то пряма а і коло мають одну спільну точку (дотична до кола).

3) Якщо відстань від центра кола до прямої дорівнює 8 см, то пряма а і коло не мають жодної спільної точки (не перетинаються).

Завдання 644

Радіус кола дорівнює 3 дм.

1) Якщо відстань від центра кола до прямої дорівнює 3,7 дм, то пряма b і коло не мають жодної спільної точки (не перетинаються).

2) Якщо відстань від центра кола до прямої дорівнює 3 дм, то пряма b і коло мають одну спільну точку (дотична до кола).

3) Якщо відстань від центра кола до прямої дорівнює 2,7 дм, то пряма b і коло мають дві спільні точки (січна до кола).

Завдання 645 Малюнок 22.7

1) KP – дотична до кола, точка O – центр кола. Знайдіть ∠OMN, якщо ∠NMP = 40°.

За умовою КР – дотична, ∠ОМР = 90°, тому ∠OMN = ∠OMP – ∠NMP = 90° – 40° = 50°.

Відповідь: 50°.

2) KP – дотична до кола, точка O – центр кола. Знайдіть ∠KMN, якщо ∠OMN = 48°.

За умовою КР – дотична, ∠KМO = 90°, тому ∠KMN = ∠KMO + ∠OMN = 90° + 48° = 138°.

Відповідь: 138°.

Завдання 646 Малюнок 22.7

1) KP – дотична до кола, точка O – центр кола. Знайдіть ∠NMP, якщо ∠OMN = 53°.

За умовою КР – дотична, ∠ОМР = 90°, тому ∠NMP = ∠OMP – ∠OMN = 90° – 53° = 37°.

Відповідь: 37°.

1) KP – дотична до кола, точка O – центр кола. Знайдіть ∠OMN, якщо ∠KMN = 130°.

За умовою КР – дотична, ∠ОМР = 90°, тому ∠OMN = ∠KMN – ∠OMP = 130° – 90° = 40°.

Відповідь: 40°.

Завдання 647

З точки A до кола із центром у точці O проведено дві дотичні AB і AC (B і C – точки дотику). Доведіть, що промінь OA – бісектриса кута BOC.

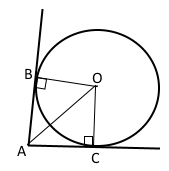
За умовою АВ і АС – дотичні, то ∠А = ∠B = 90°, ОВ = ОС – радіуси кола. Проведемо промінь АО. Трикутники АВО і АСО – прямокутні, де АО – спільні гіпотенузи. За катетом і гіпотенузою ∆АВО = ∆АСО, тому відповідні кути рівні ∠ВАО = ∠САО, промінь АО проходить між сторонами кута ВАС, причому ∠ВАС = 2∠ВАО або ∠ВАС = 2∠ВАО. Отже, промінь OA – бісектриса кута BOC.

Завдання 648

З точки P до кола із центром у точці Q проведено дотичні PM і PN. Доведіть, що промінь PQ – бісектриса кута MPN.

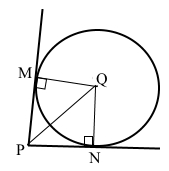
За умовою PM і PN – дотичні, то ∠M = 90° і ∠N = 90°, QM = QN – радіуси кола. Проведемо промінь PQ. Трикутники MPQ і NPQ – прямокутні, де PQ – спільні гіпотенузи. За катетом і гіпотенузою ∆PMQ = ∆PNQ, тому відповідні кути рівні ∠MPQ = ∠NPQ, промінь PQ проходить між сторонами кута MPN, причому ∠MPN = 2∠MPQ або ∠MPN = 2∠NPQ. Отже, промінь PQ – бісектриса кута BOC.

Завдання 649 Малюнок 22.8

Пряма MK – дотична до кола , точка O – центр кола. Знайдіть ∠NMK, якщо ∠MON = 82°.

О – центр кола, MN – хорда, а ОМ = ON – радіуси. Трикутник MON – рівнобедрений з основою MN, тому ∠OMN = ∠ONM, згідно теореми про суму кутів трикутника ∠OMN = (180° – ∠MON) : 2 = (180° – 82°) : 2 = 49°.

За умовою МК – дотична до кола в точці М, то ∠ОМК = 90°, згідно властивості вимірювання кутів ∠NMK = ∠OMK – ∠OMN = 90° – 49° = 41°.

Відповідь: 41°.

Завдання 650 Малюнок 22.8

Пряма MK – дотична до кола, точка O – центр кола. Знайдіть ∠NOM, якщо ∠KMN = 53°.

За умовою МК – дотична до кола в точці М, то ∠ОМК = 90°, згідно властивості вимірювання кутів ∠OMN = ∠OMK – ∠KMN = 90° – 53° = 37°.

О – центр кола, MN – хорда, а ОМ = ON – радіуси. Трикутник MON – рівнобедрений з основою MN, тому ∠OMN = ∠ONM, згідно теореми про суму кутів трикутника ∠NOM = (180° – 2∠OMN) = (180° – 37° • 2) : 2 = 106°.

Відповідь: 106°.

Завдання 651

З точки M, що лежить поза колом, проведено дві дотичні. Відстань від точки M до центра кола вдвічі більша за радіус кола. Знайдіть кут між дотичними.

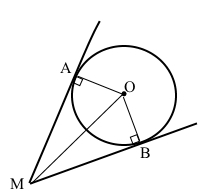
За умовою МА і МВ – дотичні, тому ОА = ОВ – радіуси і ∠А = ∠В = 90°. Трикутники МАО і МВО – прямокутні, МО – їхня гіпотенуза, АО і ОВ – катети, які дорівнюють половині гіпотенузи, тому проти цих катетів лежать кути ∠АМО = ∠ВМО = 30°. За властивістю вимірювання кутів ∠АМВ = ∠АМО + ∠ВМО = 30° + 30° = 60°.

Відповідь: 60°.

Завдання 652

Прямі MN і MK дотикаються до кола із центром O в точках N і K. Знайдіть NK, якщо ∠OMN = 30°, MN = 7 см.

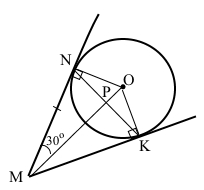
За умовою МN і МK – дотичні, які проведені з одної точки М , тому відрізки дотичних MN = МК = 7 см, також ОN = ОK – радіуси і ∠N = ∠K = 90°. Трикутники OMN і OMK – прямокутні, МО – спільна гіпотенуза, катети ON = OK, тому ∆OMN = ∆OMK (за катетом і гіпотенузою). Звідси відповідні кути ∠OMN = ∠OMK = 30°. Трикутник NMK – рівнобедрений, МО – бісектриса є висотою (∆PMN – прямокутний) і медіаною (РN = PK). Катет PN = MN/2 (катет проти кута 30°), також основа РК = 2PN = 2 (MN/2) = MN = 7 см.

Відповідь: 7 см.

Вправа для повторення

Завдання 653

Один з кутів трикутника дорівнює половині зовнішнього кута, не суміжного з ним. Доведіть, що трикутник рівнобедрений.

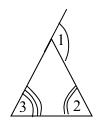
За умовою ∠1 – зовнішній кут, ∠2 = ½∠1, тоді ∠1 = 2∠2 = ∠2 + ∠2. За властивістю зовнішнього кута ∠1 = ∠2 + ∠3, звідси ∠2 = ∠3, отже, трикутник рівнобедрений (за ознакою рівних кутів).

Завдання 654 Малюнок 22.9

∠C = 90°, ∠ABC = 30°, ∠ADB = 15°, AC = 6 см. Знайдіть BD.

За умовою ∠C = 90°, трикутник АВС – прямокутний. Оскільки катет АС = 6 см = АВ/2 (катет проти кута 30°), АВ = 2 АС = 2 • 6 см = 12 см.

Кут СВА – зовнішній для кута ∠ABD трикутника ABD, звідси ∠DAB = ∠ABC – ∠ADB = 30° – 15° = 15°, ∠DAB = ∠ADB = 15°, трикутник ABD – рівнобедрений (ознака за двома рівними кутами), отже BD = BA = 12 см.

Відповідь: 12 см.

Життєва математика

Завдання 655

Для того щоб визначити відстань від спостерігача B до недоступного дерева A, що росте на другому березі, було виконано побудови. Як тепер можна знайти відстань BA?

За умовою ∠C = ∠C₁ = 90°, трикутники АВС і А₁BC₁ – прямокутні, АС = А₁С, вертикальні кути ∠ABC = ∠A₁BC₁, трикутники ∆АВС = ∆А₁BC₁ (за катетом і прилеглим кутом), отже BA = B₁A. При такій побудові відстань через озеро можна виміряти на березі.

Завдання 656

Поставте п'ять шашок на шахову дошку (розмір якої 8 х 8) так, щоб будь-який квадрат, що складається з дев'яти клітинок, містив тільки одну шашку.