ГДЗ геометрія 7 клас Істер взаємне розміщення двох кіл

Інші завдання дивись тут...

Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."

(умови завдань з підручника подані чорним кольором)

§26 Взаємне розміщення двох кіл

Завдання 719

На малюнку 26.5 два кола перетинаються.

На малюнку 26.6 два кола дотикаються (зовнішній дотик).

На малюнку 26.7 два кола не перетинаються.

Завдання 720

1) Накресліть два кола, радіуси яких дорівнюють 3 см і 2 см, так, щоб вони мали внутрішній дотик.

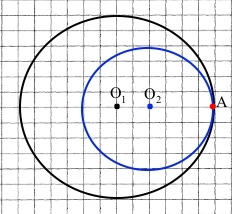
Точка А – точка дотику.

Нехай О₁О₂ – відстань між центрами кіл.

Щоб дотик був внутрішнім, кола повинні знаходитися по одну сторону дотичної прямої кіл, а відстань О₁О₂ = 3 см – 2 см.

2) Накресліть два кола, радіуси яких дорівнюють 3 см і 2 см, так, щоб вони перетиналися.

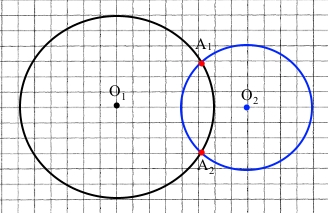
Точки А₁ і А₂ – точки дотику.

Нехай О₁О₂ – відстань між центрами кіл.

Щоб кола перетиналися, повинна виконуватися нерівність трикутника для відстані між центрами кіл.

3 см – 2 см < О₁О₂ < 3 см + 2 см

1 см < О₁О₂< 5 см

Нехай відстань О₁О₂дорівнює 4 см.

3) Накресліть два кола, радіуси яких дорівнюють 3 см і 2 см, так, щоб вони були концентричними.

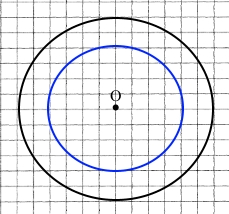
Щоб кола були концентричними, вони повинні мати спільний центр.

О = О₁ = О₂

Концентричні кола не перетинаються.

Завдання 721

1) Накресліть два кола, радіуси яких дорівнюють 2 см і 1,5 см, так, щоб вони мали зовнішній дотик.

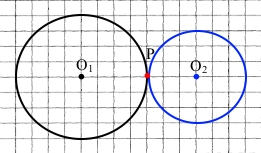
Точка Р – точка дотику.

Нехай О₁О₂ – відстань між центрами кіл.

Щоб дотик був зовнішнім, кола повинні знаходитися по різні сторони від дотичної прямої кіл, а О₁О₂ = 2 см + 1,5 см = 3,5 см.

2) Накресліть два кола, радіуси яких дорівнюють 2 см і 1,5 см, так, щоб вони не перетиналися.

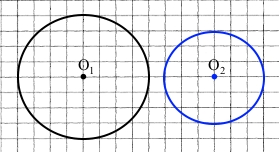
Нехай О₁О₂ – відстань між центрами кіл.

Щоб кола не перетиналися, О₁О₂ > 2 см + 1,5 см

Наприклад, О₁О₂ = 4 см.

Завдання 722

Накресліть відрізок 4 см завдовжки. Побудуйте два кола, що мають зовнішній дотик, центрами яких є кінці цього відрізка.

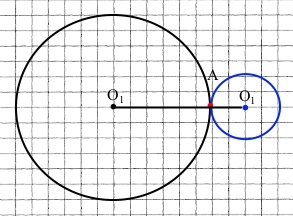
Нехай О₁О₂ = 4 см – відстань між центрами кіл.

Щоб дотик був зовнішнім, кола повинні знаходитися по різні сторони від дотичної прямої кіл, а О₁О₂ = 4 см = 3 см + 1 см, де r₁ = 3 см, r₂ = 1 см.

Точка А – точка дотику.

Завдання 723

Накресліть відрізок 2 см завдовжки. Побудуйте два кола, що мають внутрішній дотик, центрами яких є кінці цього відрізка.

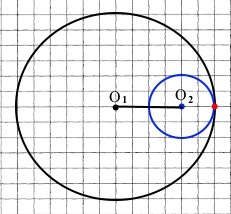
Нехай О₁О₂ = 2 см – відстань між центрами кіл.

Щоб дотик був внутрішнім, кола повинні знаходитися по одну сторону дотичної прямої кіл, а відстань О₁О₂ = 2 см = 3 см – 1 см.

Точка А – точка дотику.

Завдання 724

1) Радіуси двох кіл дорівнюють 7 см і 5 см. Знайдіть відстань між їхніми центрами, якщо кола мають внутрішній дотик.

За умовою r₁ = 7 см, r₂ = 5 см, О₁О₂ – відстань між центрами кіл.

Якщо кола мають внутрішній дотик, тоді справджується рівність:

О₁О₂ = r₁ – r₂ = 7 см – 5 см = 2 см

Відповідь: 2 см.

2) Радіуси двох кіл дорівнюють 7 см і 5 см. Знайдіть відстань між їхніми центрами, якщо кола мають зовнішній дотик.

За умовою r₁ = 7 см, r₂ = 5 см, О₁О₂ – відстань між центрами кіл.

Якщо кола мають зовнішній дотик, тоді справджується рівність:

О₁О₂ = r₁ + r₂ = 7 см + 5 см = 12 см

Відповідь: 12 см.

Завдання 725

1) Радіуси двох кіл дорівнюють 3 см і 8 см. Знайдіть відстань між їхніми центрами, якщо кола мають зовнішній дотик.

За умовою r₁ = 3 см, r₂ = 8 см, О₁О₂ – відстань між центрами кіл.

Якщо кола мають зовнішній дотик, тоді справджується рівність:

О₁О₂ = r₁ + r₂ = 3 см + 8 см = 11 см

Відповідь: 11 см.

2) Радіуси двох кіл дорівнюють 3 см і 8 см. Знайдіть відстань між їхніми центрами, якщо кола мають внутрішній дотик.

За умовою r₁ = 3 см, r₂ = 8 см, О₁О₂ – відстань між центрами кіл.

Якщо кола мають внутрішній дотик, тоді справджується рівність:

О₁О₂ = r₁ – r₂ = 8 см – 3 см = 5 см

Відповідь: 5 см.

Завдання 726

Два кола мають внутрішній дотик. Відстань між їхніми центрами дорівнює 12 дм. Знайдіть радіуси кіл, якщо вони відносяться як 2 : 5.

Якщо кола мають внутрішній дотик, тоді справджується рівність О₁О₂ = r₁ – r₂.

Нехай 2х (дм) – радіус меншого кола, 5х (дм) – радіус більшого кола.

Складемо рівняння.

5х – 2х = 12

3х = 12

х = 12 : 3

х = 4 (дм) – 1 частина.

2х = 4 • 2 = 8 (дм) – радіус меншого кола.

5х = 4 • 5 = 20 (дм) – радіус більшого кола.

Відповідь: 8 дм, 20 дм.

Завдання 727

Два кола мають зовнішній дотик. Відстань між їхніми центрами дорівнює 15 см. Знайдіть радіуси кіл, якщо вони відносяться як 2 : 3.

Якщо кола мають внутрішній дотик, тоді справджується рівність О₁О₂ = r₁ + r₂.

Нехай 2х (см) – радіус меншого кола, 3х (см) – радіус більшого кола.

Складемо рівняння.

2х + 3х = 15

5х = 15

х = 15 : 5

х = 3 (см) – 1 частина.

2х = 3 • 2 = 6 (см) – радіус меншого кола.

3х = 3 • 3 = 9 (см) – радіус більшого кола.

Відповідь: 6 см, 9 см.

Завдання 728

1) Відстань між центрами двох кіл дорівнює 12 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють 9 см і 3 см.

За умовою r₁ = 9 см, r₂ = 3 см, О₁О₂ = 12 см – відстань між центрами кіл.

12 см = 9 см + 3 см

О₁О₂ = r₁ + r₂

Кола мають зовнішній дотик.

2) Відстань між центрами двох кіл дорівнює 12 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють 5 см і 2 см.

За умовою r₁ = 5 см, r₂ = 2 см, О₁О₂ = 12 см – відстань між центрами кіл.

12 см > 5 см + 2 см

О₁О₂ > r₁ + r₂

Кола не перетинаються.

3) Відстань між центрами двох кіл дорівнює 12 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють 13 см і 1 см.

За умовою r₁ = 13 см, r₂ = 1 см, О₁О₂ = 12 см – відстань між центрами кіл.

12 см = 13 см – 1 см

О₁О₂ = r₁ – r₂

Кола мають внутрішній дотик.

4) Відстань між центрами двох кіл дорівнює 12 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють 9 см і 7 см.

За умовою r₁ = 9 см, r₂ = 7 см, О₁О₂ = 12 см – відстань між центрами кіл.

9 см – 7 см < 12 см < 9 см + 7 см

r₁ + r₂ < О₁О₂< r₁ – r₂

Кола перетинаються (мають дві спільні точки).

Завдання 729

1) Відстань між центрами двох кіл дорівнює 14 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють 7 см і 5 см.

За умовою r₁ = 7 см, r₂ = 5 см, О₁О₂ = 14 см – відстань між центрами кіл.

14 см > 7 см + 5 см

О₁О₂ > r₁ + r₂

Кола не перетинаються.

2) Відстань між центрами двох кіл дорівнює 14 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють 16 см і 2 см.

За умовою r₁ = 16 см, r₂ = 2 см, О₁О₂ = 14 см – відстань між центрами кіл.

14 см = 16 см – 2 см

О₁О₂ = r₁ – r₂

Кола мають внутрішній дотик.

3) Відстань між центрами двох кіл дорівнює 14 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють 10 см і 5 см.

За умовою r₁ = 10 см, r₂ = 5 см, О₁О₂ = 14 см – відстань між центрами кіл.

10 см – 5 см < 14 см < 10 см + 5 см

r₁ + r₂ < О₁О₂< r₁ – r₂

Кола перетинаються (мають дві спільні точки).

4) Відстань між центрами двох кіл дорівнює 14 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють 7 см і 7 см.

За умовою r₁ = 7 см, r₂ = 7 см, О₁О₂ = 14 см – відстань між центрами кіл.

14 см = 7 см + 7 см

О₁О₂ = r₁ + r₂

Кола мають зовнішній дотик.

Завдання 730

Два кола перетинаються в точках A і B. Точки О₁ і О₂ – центри цих кіл. Доведіть, що О₁О₂ ﬩ AB.

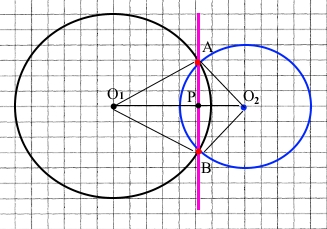
За умовою О₁А = О₁B – радіуси кола з центром у точці О₁, О₂А = О₂В – радіуси кола з центром у точці О₂. О₁О₂ – спільна сторона трикутників О₁АО₂ і О₁ВО₂, тому ∆О₁АО₂ = ∆О₁ВО₂ (за третьою ознакою рівності трикутників), відповідні кути АО₁О₂ = ВО₁О₂, АО₂О₁ = ВО₂О₁, тому О₁О₂ – бісектриса кута АО₁В і кута АО₂В.

Проведемо відрізок АВ, позначимо точку Р перетину АВ і О₁О₂.

Трикутники АО₁В і АО₂В – рівнобедрені зі сторонами, які дорівнюють відповідним радіусам (за означенням), бісектриса є висотою О₁Р ﬩ АВ, О₂Р ﬩ АВ, оскільки через точку площини проходить тільки одна пряма, перпендикулярна до даної, отже О₁О₂ ﬩ АВ, що треба було довести.

Завдання 731

Два кола перетинаються в точках C і D. Точки О₁ і О₂ – центри кіл. Доведіть, що промінь О₁О₂ – бісектриса кута CО₁D.

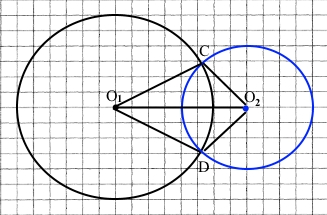
За умовою О₁C = О₁D – радіуси кола з центром у точці О₁, О₂C = О₂D – радіуси кола з центром у точці О₂. О₁О₂ – спільна сторона трикутників О₁CО₂ і О₁DО₂, тому ∆О₁CО₂ = ∆О₁DО₂ (за третьою ознакою рівності трикутників), відповідні кути CО₁О₂ = DО₁О₂, або CО₁D = 2СО₁О₂, тому О₁О₂ – бісектриса кута СО₁D, що треба було довести.

Завдання 732

Три кола попарно мають зовнішній дотик. Відрізки, що сполучають їхні центри, утворюють трикутник зі сторонами 5 см, 7 см і 8 см. Знайдіть радіуси цих кіл.

Нехай r₁, r₂, r₃ – радіуси кіл з відповідними центрами О₁, О₂, О₃.

За умовою три кола мають попарно зовнішній дотик, тоді справедливі рівності:

О₁О₂ = r₁ + r₂ = 5 см О₂О₃ = r₂ + r₃ = 7 см О₃О₁ = r₃ + r₁ = 8 см

{r₁ + r₂ = 5

r₂ + r₃ = 7

r₃ + r₁ = 8

{r₁ = 5 – r₂

r₃ = 7 – r₂

(7 – r₂) + (5 – r₂) = 8

Розв'язуємо рівняння:

(7 – r₂) + (5 – r₂) = 8

7 – r₂ + 5 – r₂ = 8

7 + 5 – 8 = 2r₂

2r₂ = 4

r₂ = 4 : 2

r₂ = 2

Знайдене значення змінної r2 підставляємо в рівняння r₁ = 5 – r₂:

r₁ = 5 – 2

r₁ = 3

Знайдене значення змінної r2 підставляємо в рівняння r₃ = 7 – r₂:

r₃ = 7 – 2

r₃ = 5

Відповідь: 3 см, 2 см, 5 см.

Завдання 733

Три кола попарно дотикаються зовні. Радіус одного з кіл дорівнює 6 см, а відрізок, що сполучає центри двох інших кіл, дорівнює 14 см. Знайдіть периметр трикутника, вершинами якого є центри цих кіл.

Нехай r₁ = 6 см, r₂, r₃ – радіуси кіл з відповідними центрами О₁, О₂, О₃.

О₁О₂ = r₁ + r₂

О₂О₃ = r₂ + r₃ = 14 см

О₃О₁ = r₃ + r₁

За умовою три кола мають попарно зовнішній дотик, тоді справедливі рівності.

Р = О₁О₂+ О₂О₃+ О₃О₁= r₁ + r₂+ r₂ + r₃ + r₃ + r₁ = 2r₁ + 2r₂+ 2r₃ = 2(r₁ + r₂ + r₃) = 2 • (6 + 14) = 40 (см).

Відповідь: Р = 40 см.

Вправи для повторення

Завдання 734

У прямокутному трикутнику ABC гіпотенуза AB дорівнює 20 см, ∠B = 60°. Довжину якого з катетів можна знайти? Знайдіть її.

Можна знайти довжину катета, який знаходиться проти кута 30°.

Проти гіпотенузи АВ знаходиться прямий кут ∠С = 90°, тоді ∠А = 30°. Проти кута А знаходиться катет ВС = ½ АВ = 20 см : 2 = 10 см.

Завдання 735

Коло вписано в чотирикутник ABCD (дотикається до всіх його сторін). Доведіть, що AB + CD = AD + BC.

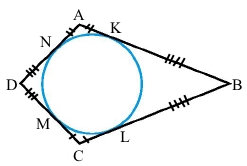
Точки K, L, M, N – точки дотику, які належать відповідній стороні.

За властивістю вимірювання відрізків AB = KA + KB, CD = MC + MD, AD = NA + ND, BC = LB + LC.

За властивістю дотичних до кола проведених з одної точки маємо рівні пари відрізків: KB = LB, KA = NA, ND = MD, MC = LC.

Перевіримо рівність AB + CD = KA + KB + MC + MD = NA + LB + LC + ND = (NA + ND) + (LB + LC) = AD + BC. Отже, AB + CD = AD + BC, що треба було довести.

Життєва математика

Завдання 736

Приватна підприємиця має три магазини, розміщені в точках A, B і C, які не лежать на одній прямій. Вона хоче побудувати склад так, щоб відстань від нього до всіх магазинів була однаковою. Де має бути розміщений цей склад?

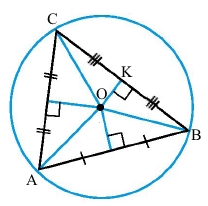
1) На плані відрізками сполучаємо знаки магазинів так, щоб вони були вершинами трикутника.

2) Проводимо серединні перпендикуляри до сторін трикутника (достатньо до двох).

3) Точка перетину серединних перпендикулярів – центр кола, описаного навколо трикутника. Там треба розмістити склад, щоб він був рівновіддаленим від вершин трикутника (магазинів).

Цікаві задачі

Завдання 737

Прямокутник поділено на дев'ять прямокутників. Периметри трьох з них відомі, і їх вказано на малюнку. Знайдіть периметр зафарбованого прямокутника.