© Барна Р., 2020
Серія "Вчимось разом" до підручника "Математика 3 клас Заїка А., Тарнавська С."
Завдання 1 Всього десятків у числах
У числі 350 всього 35 десятків, у числі 470 всього 47 десятків, у числі 520 всього 52 десятки, у числі 280 всього 28 десятків, у числі 660 всього 66 десятків, у числі 710 всього 71 десяток, у числі 890 всього 89 десятків.
Завдання 2 Порозрядне додавання з переходом через десяток
|
24 + 6 = 20 + 10 = 30 240 + 60 = 200 + 100 = 300 37 + 3 = 30 + 10 = 40 370 + 30 = 300 + 100 = 400 |
31 + 9 = 30 + 10 = 40 310 + 90 = 300 + 100 = 400 55 + 5 = 50 + 10 = 60 550 + 50 = 500 + 100 = 600 |
46 + 15 = 61 460 + 150 = 610 48 + 24 = 72 480 + 240 = 720 |
Завдання 3 Проста задача на додавання
На заправці у першій бензоколонці 580 л бензину, а в другій – 240 л. Скільки всього літрів бензину?
|
І бензоколонка |
ІІ бензоколонка |
Всього |
|
580 л |
240 л |
? |
Короткий запис
І бензоколонка — 580 л
ІІ бензоколонка — 240 л
Всього — ?
Схема
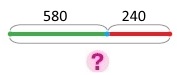
Розв’язання
580 + 240 = 700 + 120 = 820 (л) – всього літрів бензину.
Відповідь: всього 820 літрів бензину.
Завдання 4
Порозрядне додавання з переходом через десяток:
580 + 240 = (500 + 80) + (200 + 40) = (500 + 200) + (80 + 40) = 700 + 120 = 820
Додавання частинами:
580 + 240 = 580 + (200 + 40) = (580 + 200) + 40 = 780 + 40 = 820
Укрупнення розрядних доданків:
580 + 240 = 58 дес. + 24 дес. = 82 дес. = 820
Завдання 5
|
630 + 90 = 720 90 + 630 = 720 |
770 + 70 = 840 70 + 770 = 840 |
870 + 40 = 910 40 + 870 = 910 |
Завдання 6
Порозрядне додавання з переходом через десяток:
270 + 140 = (200 + 100) + (70 + 40) = 300 + 110 = 410
380 + 360 = (300 + 300) + (80 + 60) = 600 + 140 = 740
Порозрядне віднімання: 270 – 140 = 130 380 – 360 = 20
458 – 58 = 400 458 – 408 = 50 840 – 600 = 240
Порозрядне додавання: 140 + 300 = 440
Рівність порівняння першого і останнього виразів:
270 + 140 < 140 + 300 (сума чисел 270 і 140 менша, ніж сума чисел 140 і 300)
Завдання 7
а) В одному селі проживає а людей, а в сусідньому — b людей. Скільки людей проживає в обох селах?
а + b (л.)
Якщо а = 520, b = 390, тоді а + b = 520 + 390 = 520 + 80 + 310 = 910 (л.)
б) На першій вулиці села а будинків, на другій — на 20 будинків менше. Скільки будинків на другій вулиці? Скільки будинків на двох вулицях?
а – 20 (б.) – будинків на другій вулиці.
а + (а – 20) (б.) – будинків на двох вулицях.
Якщо а = 80, тоді а – 20 = 80 – 20 = 60 (б.)
Якщо а = 80, тоді а + (а – 20) = 80 + (80 – 20) = 80 + 60 = 140 (б.)
Завдання 8, 9 Округлення чисел до найближчої сотні
180 ≈ 200 325 ≈ 300 570 ≈ 600 640 ≈ 600
290 ≈ 300 310 ≈ 300 580 ≈ 600
Завдання 10 Додавання способом округлення
580 + 240 = (600 – 20) + 240 = 600 + 240 – 20 = 840 – 20 = 820
620 + 190 = (620 + (200 – 190) = 620 + 200 – 10 = 820 – 10 = 810
340 + 290 = 340 + (300 – 10) = 340 + 300 – 10 = 640 – 10 = 630
490 + 360 = (500 – 10) + 360 = 500 + 360 – 10 = 860 – 10 = 850
Завдання 11 У прямокутнику АВСВ сторона ВС = 8 см, а периметр Р = 20 см. Обчисли довжину сторони АВ.
Розв’язання
Вираз (20 : 2) – 8
1) 20 : 2 = 10 (см) – півпериметр (сума довжини і ширини).
2) 10 – 8 = 2 (см) – довжина сторони АВ.
Відповідь: довжина сторони АВ дорівнює 2 см.
Завдання 12 Периметр прямокутника 18 см, а його ширина 4 см. Яка довжина прямокутника?
Розв’язання
Вираз (18 : 2) – 4
1) 18 : 2 = 9 (см) – півпериметр (сума довжини і ширини).
2) 9 – 4 = 5 (см) – довжина прямокутника.
Відповідь: довжина прямокутника 5 сантиметрів.
Поділили прямокутник довжиною 5 см і шириною 4 см на 20 рівних частин
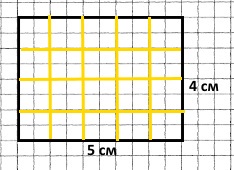
Завдання 13 Порядок дій
380 + 350 = (400 – 20) + 350 = 400 + 350 – 20 = 750 – 20 = 730
290 + 240 = (300 – 10) + 240 = 300 + 240 – 10 = 540 – 10 = 530
470 + 190 = 470 + (200 – 100) = 470 + 200 – 10 = 670 – 10 = 660
900 – 490 = 900 – 400 – 90 = 500 – 90 = 410
800 – 360 = 800 – 300 – 60 = 500 – 60 = 440
700 – 140 = 700 – 100 – 40 = 600 – 40 = 560
2 • 9 + 3 • 8 = 18 + 24 = 30 + 12 = 42
4 • 5 + 5 • 7 = 20 + 35 = 55
6 • 7 – 3 • 4 = 42 – 12 = 30
Завдання 14 У будівлі школи 210 вікон, а дверей — на b менше. Запиши виразом, скільки дверей у будівлі. 210 – b
210 – b (в.) – дверей у будівлі.
Якщо b = 140, тоді 210 – b = 210 – 140 = 210 – 110 – 30 = 70 (в.)
� Скільки вікон і дверей у будівлі школи?
210 + (210 – b) (шт.) – всього вікон і дверей у будівлі школи.
Завдання 15
a + b = b + a (переставний закон додавання)
a • b = b • a (переставний закон множення)
Завдання 16
Рівності, у яких від'ємник містить чотири сотні
Зменшуване – Від'ємник = Різниця, 429 = 4 сот. 2 дес. 9 од., 480 = 4 сот. 8 дес.
734 – 429 = 305 460 – 380 = 80 480 – 480 = 0
Завдання 17
Якщо від’ємник збільшити на кілька одиниць, то різниця зменшиться на стільки само одиниць:
38 – 15 = 23
38 – 20 = 38 – (15 + 5) = (38 – 15) – 5 = 23 – 5 = 18
Якщо від’ємник зменшити на кілька одиниць, то різниця збільшиться на стільки само одиниць:
230 – 150 = 80
230 – 100 = 230 – (150 – 50) = (230 – 150) + 50 = 80 + 50 = 130
400 – 210 = 190
400 – 200 = 400 – (210 – 10) = (400 – 210) + 10 = 190 + 10 = 200
Завдання 18
Що дорожча покупка, то менша буде решта, якщо однакова кількість.
|
Було — 50 грн Витратили на сік — 10 грн Залишилось (решта) — 40 грн |
Було — 50 грн Витратили на сік — 40 грн Залишилось (решта) — 10 грн |
Завдання 19 У тебе 20 грн. У шкільній їдальні є пакетики соку по 5 грн і 7 грн. Який пакетик ти купиш, щоб решта була більшою?
пакетик по 5 грн
20 – 7 = 13 20 – 5 = 15 15 > 13
Завдання 20 Віднімання способом округлення
70 – 30 = 40
70 – 28 = 70 – (30 – 2) = 70 – 30 + 2 = 40 + 2 = 42
Завдання 21 Віднімання способом округлення
480 – 300 = 180
480 – 290 = 480 – (300 – 10) = 480 – 300 + 10 = 180 + 10 = 190
160 – 100 = 60
160 – 90 = 160 – (100 – 10) = 160 – 100 + 10 = 60 + 10 = 70
400 – 240 = 160
400 – 270 = 400 – (240 + 30) = 400 – 240 – 30 = 160 – 30 = 130
Завдання 22 Рівняння
|
х • 9 = 63 х = 63 : 9 х = 7 7 • 9 = 63 63 = 63 |
7 • х = 35 х = 35 : 7 х = 5 7 • 5 = 35 35 = 35 |
х – 360 = 420 х = 420 + 360 х = 780 780 – 360 = 420 420 = 420 |
730 – х = 550 х = 730 – 550 х = 180 730 – 180 = 550 550 = 550 |
Завдання 23 Лепбук «Наш клас» має форму прямокутника, довжина якого 1 м (10 дм), а ширина — у 2 рази менша. Якої довжини має бути кольорова смужка, щоб окантувати цей лепбук?
|
1 спосіб 10 : 2 = 5 (дм) – ширина лепбука Р = 10 • 2 + 5 • 2 = 20 + 10 = 30 (дм) |
2 спосіб 10 : 2 = 5 (дм) – ширина лепбука Р = (10 + 5) • 2 = 15 + 15 = 30 (дм) |
3 спосіб 10 : 2 = 5 (дм) – ширина лепбука Р = 10 + 5 + 10 + 5 = 30 (дм) |
Відповідь: довжина кольорової смужки 30 дм.
� Плакат «Таблиця множення» має форму прямокутника, довжина якого 80 см, а ширина — у 2 рази менша. Якої довжини має бути кольорова смужка, щоб окантувати цей плакат?
|
1 спосіб 80 : 2 = 40 (см) – ширина плаката Р = 80 • 2 + 40 • 2 = 160 + 80 = 240 (см) |
2 спосіб 80 : 2 = 40 (см) – ширина плаката Р = (80 + 40) • 2 = 120 + 120 = 240 (см) |
3 спосіб 80 : 2 = 40 (см) – ширина плаката Р = 80 + 40 + 80 + 40 = 240 (см) |
Завдання 24
Вираз з двома змінними а + b – 4
Числовий вираз 10 + 8 – 4 Читаємо числовий вираз: від суми чисел 10 і 8 відняти число 4.
10 + 8 – 4 = 18 – 4 = 14
Завдання 25 Натуральні числа
Круглі десятки: 120, 380, 30, 170, 560, 770
Круглі сотні: 100, 400, 200, 600, 500, 800
Завдання 26 Непряма складена задача
Василькові 9 років, він старший (більше років) за сестру на 2 роки, а мама старша за доньку на 23 роки. Скільки років мамі?
Короткий запис
Василько — 9 років, це на 2 роки більше, ніж сестра
Сестра — ?
Мама — ?, на 23 роки більше, ніж сестрі
План розв’язування
1) Скільки років сестрі?
2) Скільки років мамі?
Схема
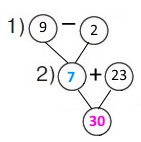
Вираз (9 – 2) + 23
Розв’язання
1) Якщо Василько на 2 роки старший від сестри, тоді сестра на 2 роки молодша, тому
9 – 2 = 7 (р.) – років сестрі.
2) 7 + 23 = 30 (р.) – років мамі.
Відповідь: мамі 30 років.
Завдання 27 Віднімання способом округлення
420 – 70 = 420 – (100 – 30) = 420 – 100 + 30 = 320 + 30 = 350
530 – 80 = 530 – (100 – 20) = 530 – 100 + 20 = 430 + 20 = 450
340 – 90 = 340 – (100 – 10) = 340 – 100 + 10 = 240 + 10 = 250
710 – 90 = 710 – (100 – 10) = 710 – 100 + 10 = 610 + 10 = 620
860 – 80 = 860 – (100 – 20) = 860 – 100 + 20 = 760 + 20 = 780