ГДЗ 4 клас робочий зошит Лишенко сторінка 79 – 86 нова програма

Інші завдання дивись тут...

Серія "Вчимось разом" до робочого зошита "Математика 4 клас Лишенко Г."

Сторінка 79

Завдання 2 Задача на зведення до одиниці

Із 200 кг картоплі виходить 40 кг крохмалю. Скільки кілограмів крохмалю вийде із 4 т (4000 кг) картоплі?

^{Короткий запис}

^{40 кг — 200}^кг

^{? кг —}^{4000 кг}

^{План розв'язування}

^{1) Скільки кілограмів крохмалю виходить з}^{20 кг картоплі? 200 : 40 = 5 (кг)}

^{2) Скільки кілограмів крохмалю вийде з 4 т? 4000 : 5 = 800 (кг)}

Розв’язання

4 т = 1 т • 4 = 1000 кг • 4 = 4000 кг

4000 : (200 : 40) = 4000 : 5 = 800 (кг)

^{2 спосіб}

^{У скільки разів більше картоплі, у стільки разів більше крохмалю.}

^{План розв’язування}

^{1) У скільки разів більше картоплі? 4000 : 200 = 40 : 2 = 20 (р.)}

^{2) Скільки кілограмів крохмалю вийде? 40 • 20 = 800 (кг)}

^{Розв’язання}

^{40 • (4000 : 200) = 40 • 20 = 800 (кг)}

Завдання 3 Рівняння

х • 400 = 72 000

^{х = 72 000 : 400}

^{х = (40 000 + 32 000) : 400}

х = 180

270 000 : х = 900

^{х = 270 000 : 900}

^{х = 2700 : 9}

х = 300

Завдання 4 Письмове множення

х 236

1888

1180

13688

х 309

1854

2472

26574

х2075

16600

4150

58100

Завдання 5

Від однієї пристані одночасно в протилежних напрямках рушили два катери. Швидкість першого катера за течією річки 32 км/год, а другого проти течії — становить 7/8 швидкості першого. Яка відстань буде між ними через 3 год?

Розв'язання

^{1 спосіб}

1) 32 : 8 • 7 = 28 (км/год) – швидкість другого катера.

2) 28 + 32 = 60 (км/год) – швидкість віддалення катерів.

3) 60 • 3 = 180 (км)

^{2 спосіб}

1) 32 : 8 • 7 = 28 (км/год) – швидкість другого катера.

2) 32 • 3 = 96 (км) – кілометрів пропливе перший катер.

3) 28 • 3 = 84 (км) – кілометрів пропливе другий катер.

4) 96 + 84 = 180 (км)

Відповідь: між катерами буде відстань 180 кілометрів.

Завдання 6

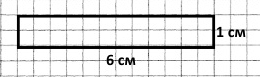
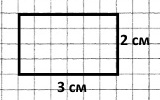
Накресли 2 різних прямокутники з площею 6 см². Обчисли та порівняй їх периметри.

6 см² = 6 см • 1 см	6 см² = 3 см • 2 см

Р = (6 + 1) • 2 = 14 (см) – периметр прямокутника довжиною 6 см і шириною 1 см.

Р = (3 + 2) • 2 = 8 (см) – периметр прямокутника довжиною 3 см і шириною 2 см.

14 см > 8 см

Сторінка 80 До № 544 – 565

Завдання 1

Володимир Великий князював у 980—1015 роках. Скільки років Володимир Великий був князем Київської Русі?

Розв'язання

1015 – 980 + 1 = 1016 – 1000 + 20 = 36 (р.) – років князював Володимир Великий.

Відповідь: був князем 36 років.

Завдання 2 Задача на зведення до одиниці

Із а т соняшнику виходить 2700 кг олії. Скільки кілограмів олії вийде з 30 т (3000 кг) соняшнику?

^{Короткий запис}

^{2700 кг — а • 1000 кг}

^{? кг — 30000 кг}

^{План розв’язування}

^{1) Скільки кілограмів олії вийде з тонни соняшнику? 1000 •}^{а : 2700 (кг)}

^{2) Скільки кілограмів олії вийде з трьох тонн соняшнику? 3000 : (1000 • а : 2700) кг}

30000 : (1000 • а : 2700)

Завдання 3 Складена задача на збільшення у декілька разів

Для облаштування парку привезли 600 саджанців лип і 400 саджанців дубів. Їх розсадили в ряди порівну. Лип посадили на 5 рядів більше. Скільки посадили рядів лип і рядів дубів?

^{Саджанці}	^{Саджанців у 1 ряді}	^{Кількість рядів}	^{Загальна кількість саджанців}
^Липи	^?	^?^{, на 5 рядів більше}	^{600, на}^?^{саджанців більше}
^Дуби	^{однаково}	^?	⁴⁰⁰

Розв'язання

1) 600 – 400 = 200 (с.) – на стільки більше привезли саджанців лип, ніж дубів.

2) 200 : 5 = 40 (с.) – саджанців посадили в одному ряді.

3) 400 : 40 = 10 (р.) – рядів саджанців дуба.

4) 10 + 5 = 15 (р.) – рядів саджанців лип.

^{2 спосіб}

^{1) 600 – 400 = 200 (с.) – на стільки більше привезли саджанців лип, ніж дубів.}

^{2) 200 : 5 = 40 (с.) – саджанців посадили в одному ряді.}

^{3) 400 : 40 = 10 (р.) – рядів саджанців дуба.}

^{4) 600 : 40 = (400 + 200) : 40 = 15 (р.) – рядів саджанців лип.}

Відповідь: 15 рядів саджанців липи, 10 рядів саджанців дуба.

Завдання 4 Порядок дій

(83 607 – 3 085 • 23) • 768 = 9 716 736

х3085

9255

6170

70955

_83607

70955

12652

х 12652

768

101216

75912

88564

9716736

Завдання 5 Постав знаки арифметичних дій.

4000 : 80 • 6 = 400 : 8 • 6 = 50 • 6 = 300 (620 – 400) • 2 = 220 • 2 = 440

Сторінка 81 До № 566 – 577

Завдання 1

х 2635

326

15810

5270

7905

859010

х 5307

408

42456

21228

2165256

х 12065

509

108585

60325

6141085

Завдання 2 Складена задача на збільшення у декілька разів

З першого поля зібрали 90 ц гречки, а з другого, площа якого на 4 га більша, — 150 ц. Знайди площі полів, якщо врожайність на обох полях однакова.

^Поле	^{Маса з 1 га (ц)}	^{Кількість га}	^{Загальна маса (ц)}
^І	^{однаково}	^?	⁹⁰
^ІІ	^?	^?^{, на 4 га більше}	^{150, на}^?^{ц більше}

Розв'язання

1) 150 – 90 = 60 (ц) – на стільки більше центнерів зібрали з другого поля.

2) 60 : 4 = 15 (ц) – центнерів зібрали з 1 гектару.

3) 90 : 15 = 90 : 3 : 5 = 6 (га) – площа першого поля.

4) 6 + 4 = 10 (га) – площа другого поля.

^{2 спосіб}

^{1) 150 – 90 = 60 (ц) – на стільки більше центнерів зібрали з другого поля.}

^{2) 60 : 4 = 15 (ц) – центнерів зібрали з 1 гектару.}

^{3) 90 : 15 = 90 : 3 : 5 = 6 (га) – площа першого поля.}

^{4) 150 : 15 = 10 (га) – площа другого поля.}

Відповідь: площа першого поля 6 гектарів, другого – 10 гектарів.

Завдання 3 Множення

7 • 3 = 21 С	6 • 2 = 12 І	7 • 5 = 35 М
6 • 3 = 18 Р	8 • 2 = 16 А	8 • 4 = 32 З	6 • 2 = 12 І	7 • 2 = 14 В
6 • 4 = 24 В	6 • 2 = 12 І	6 • 5 = 30 Д	7 • 5 = 35 М	6 • 2 = 14 І	6 • 3 = 18 Р
9 • 3 = 27 О	6 • 5 = 30 Д	7 • 4 = 28 И	8 • 5 = 40 Н
6 • 3 = 18 Р	8 • 2 = 16 А	8 • 4 = 32 З
7 • 2 = 14 В	6 • 2 = 12 І	6 • 5 = 30 Д	6 • 3 = 18 Р	6 • 2 = 12 І	9 • 5 = 45 Ж

Сторінка 82 До 578 – 597

Завдання 1 Ділення

180 : (3 • 5) = 180 : 3 : 5 = 60 : 5 = (50 + 10) : 5 = 10 + 2 = 12

540 : (5 • 6) = 540 : 6 : 5 = 90 : 5 = (50 + 40) : 5 = 10 + 8 = 18

3900 : (5 • 13 • 30) = 3900 : 30 : 13 : 5 = 130 : 13 : 5 = 10 : 5 = 2

Завдання 2 Складена задача на збільшення у декілька разів

На пошиття синіх костюмів витратили 972 м тканини, а на коричневі, яких пошили на 9 костюмів більше, витратили 999 м тканини. Скільки пошили костюмів, якщо витрати тканини на один костюм однакові?

^{Костюми}	^{Довжина тканини на 1 костюм (м)}	^{Кількість костюмів}	^{Загальна довжина тканини (м)}
^Сині	^{однаково}	^?	⁹⁷²
^{Коричневі}	^?	^?^{, на 9 костюмів більше}	^{999, на}^?^{м більше}

Розв'язання

1) 999 – 972 = 27 (м) – на стільки більше метрів тканини витратили на коричневі костюми.

2) 27 : 9 = 3 (м) – метрів тканини витрачають на один костюм.

3) 972 : 3 = (900 + 60 + 12) : 3 = 324 (к.) – синіх костюмів пошили.

4) 324 + 9 = 324 + 6 + 3 = 333 (к.) – коричневих костюмів пошили.

^{2 спосіб}

^{1) 999 – 972 = 27 (м) – на стільки більше метрів тканини витратили на коричневі костюми.}

^{2) 27 : 9 = 3 (м) – метрів тканини витрачають на один костюм.}

^{3) 972 : 3 = (900 + 60 + 12) : 3 = 324 (к.) – синіх костюмів пошили.}

^{4) 999 : 3 = (900 + 90 + 9) : 3 = 333 (к.) – коричневих костюмів пошили.}

Відповідь: пошили 324 синіх і 333 коричневих костюмів.

Завдання 3 Ділення з остачею

Заповни пропуски, якщо відомо, що остача — найбільша з можливих.

63 : 8 = 7 (ост. 7)

^{7 < 8, 7 • 8 + 7 = 56 + 7 = 56 + 4 + 3 = 63}

89 : 9 = 9 (ост. 8)

^{8 < 9, 9 • 9 + 8 = 81 + 8 = 89}

Завдання 4

Суму невідомого числа й числа 3600 зменшили у 20 разів і одержали 840. Знайди невідоме число.

(х + 3600) : 20 = 840

х + 3600 = 840 • 20

х + 3600 = 16800

х = 16800 – 3600

х = 13200

х840

16800

_16800

3600

13200

Сторінка 83

Завдання 5

Периметр рівнобедреного трикутника, у якого дві сторони рівні, 20 см, а третя сторона на 2 см більша за кожну з двох інших. Знайди довжини сторін трикутника.

Розв’язання

1) 20 – 2 = 18 (см) – порівну тричі.

2) 18 : 3 = 6 (см) – довжина кожної бічна сторони (1 частина)

3) 6 + 2 = 8 (см) – довжина основи.

^{2 спосіб}

^{Нехай х (см) – бічна сторона, х + 2 (см) – третя основа. Складемо рівняння}

^{х + х + х + 2 = 20}

^{х + х + х = 20 – 2}

^{х • (1 + 1 + 1) = 18}

^х^{• 3 = 18}

^{х = 18 : 3 = 6 (см) – кожна бічна сторона.}

^{х + 2 = 6 + 2 = 8 (см) – довжина основи.}

Відповідь: І сторона – 6 см, ІІ сторона – 6 см, ІІІ сторона – 8 см.

До № 598 – 618

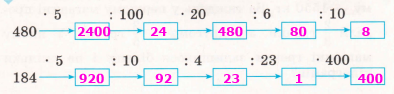
Завдання 1

⁴⁸⁰^•^{5 = (400 + 80) • 5 = 400 • 5 + 80 • 5 = 2000 + 400 = 2400 2400 : 100 = 24}

^{24 • 20 = (20 + 4) • 20 = 20 • 20 + 4 • 20 = 400 + 80 = 480 480 : 6 = 80 80 : 10 = 8}

¹⁸⁴^•^{5 = (100 + 80 + 4) • 5 = 100 • 5 + 80 • 5 + 4 • 5 = 500 + 400 + 20 = 920 920 : 10 = 92}

^{92 : 4 = (80 + 12) : 4 = 80 : 4 + 12 : 4 = 20 + 3 = 23 23 : 23 = 1 1 • 400 = 400}

Завдання 2

4236 : 80 = 52 (ост. 76)

928 : 26 = 35 (ост. 18)

_4236| 80

400 52

_236

160

_928| 26

78 35

_148

130

Завдання 3 Складена задача послідовне ділення і множення

Дві тістомішальні машини однакової потужності за З год виготовили 1608 кг тіста. Скільки кілограмів тіста виготовить одна така машина за 7 год роботи?

^{Маса за 1 год 1 машина (кг)}	^{Кількість год}	^{Кількість машин}	^{Загальна маса (кг)}
^?	³	²	¹⁶⁰⁸
^{однакова}	⁷		^?

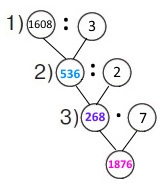
^{Вираз 1608 : 3 : 2 • 7}

Розв’язання

1) 1608 : 3 = (1500 + 90 + 18) : 3 = 536 (кг) – тіста виготовлять 2 машини 1 год.

2) 536 : 2 = (400 + 120 + 16) : 2 = 268 (кг) – тіста виготовить 1 машина за 1 год.

3) 268 • 7 = (200 + 60 + 8) • 7 = 1876 (кг) – тіста виготовить 1 машина за 7 год.

Відповідь: машина виготовить 1876 кг тіста.

Сторінка 84

Завдання 4

Довжина прямокутного спортивного майданчика 24 м, що у 2 рази більше, ніж його ширина. Знайди периметр і площу майданчика.

Розв'язання

^{Якщо довжина у 2 рази більша за ширину, тоді ширина – у 2 рази менша від довжини, тому}

1) 24 : 2 = 12 (м) – ширина прямокутного майданчика.

2) Р = (24 + 12) • 2 = 36 • 2 = 36 + 36 = 72 (м) – периметр прямокутного майданчика.

3) S = 24 • 12 = 288 (м²) – площа прямокутного майданчика.

Відповідь: Р = 72 м, S = 288 м².

Завдання 5

Хлопчика запитали, скільки йому років. Він відповів, що йому разом з братом 19 років, а 5 років тому він був у 2 рази старший за брата. Скільки років хлопчику зараз?

^{Міркуємо так.}

^{1) 19 – 10 = 9 (р.) – років хлопчикам разом 5 років тому.}

^{2) 9 : 3 = 3 (р.) – років братові 5 років тому (1 частина).}

^{3) 3 • 2 = 6 (р.) – років хлопчикові 5 років тому (2 частини).}

^{4) 6 + 5 = 11 (р.) – років хлопчикові зараз.}

Відповідь: зараз хлопчикові 11 років.

До № 619 – 639

Завдання 1

Підібрали значення букв, при яких рівності істинні.

146 • а = а

а = 0

80 • b = 80

b = 1

c • c = c

c = 0, 1

d + d = d

d = 0

2 • a = a + 6

a = 6

12 • d = d • 12

d = 0, 1, 2,…

Завдання 2 Письмове ділення

_235872 | 52

208 4536

_278

260

_187

156

_312

312

_55722 | 37

37 1506

_187

185

_222

222

Сторінка 85

Завдання 3 Складена задача на різницеве порівняння

У першому магазині було 960 кг гречки, а в другому — 1550 кг. За тиждень у першому магазині продали 2/3 гречки, а в другому — 2/5 гречки. У якому магазині гречки залишилося більше і на скільки кілограмів?

Розв'язання

^{Якщо в першому магазині продали 2/3 гречки, тоді залишилося 1/3, тому}

1) 960 : 3 • 1 = 320 (кг) – кілограмів гречки залишилось у І магазині.

^{Якщо в другому магазині продали 2/5 гречки, тоді залишилося 3/5, тому}

2) 1550 : 5 • 3 = 310 • 3 = 930 (кг) – кілограмів гречки залишилось у ІІ магазині.

3) 930 > 640 у другому магазині залишилося більше

930 – 320 = 610 (кг) – на стільки більше кілограмів гречки залишилось у І магазині, ніж у ІІ магазині.

^{2 спосіб}

^{1) 960 : 3 • 2 = 320 • 2 = 640 (кг) – кілограмів гречки продали у І магазині.}

^{2) 960 – 640 = 320 (кг) – кілограмів гречки залишилось у І магазині.}

^{3) 1550 : 5 • 2 = 310 • 2 = 620 (кг) – кілограмів гречки продали у ІІ магазині.}

^{4) 1550 – 620 = 930 (кг) – кілограмів гречки залишилось у ІІ магазині.}

^{5) 930 > 640 у другому магазині залишилося більше}

^{930 – 320 = 610 (кг) – на стільки більше кілограмів гречки залишилось у І магазині, ніж у ІІ магазині.}

Відповідь: на 610 кілограмів гречки більше залишилось у ІІ магазині.

Завдання 5

3найди закономірність і запиши пропущене число.

_431

134

297

_958

859

_424 | 53

424 8

_243 | 27

243 9

_761

745

_913

893

До № 640 – 661

Завдання 3 Ознайомлення з дробами

3/5 км = 600 м

^{3/5 км = 1 км : 5 • 3 = 1000 м : 5 • 3 = 600 м}

2/5 хв < 25 с

^{2/5 хв = 1 хв : 5 • 2 = 60 с : 5 • 2 = 24 с}

2/3 доби > 15 год

^{2/3 доби = 1 доба : 3 • 2 = 24 год : 3 • 2 = 16 год}

3/3 год > 30 хв

^{3/3 год = 1 год = 60 хв}

3/4 год < 50 хв

^{3/4 год = 1 год : 4 • 3 = 60 хв : 4 • 3 = 45 хв}

3/4 т = 750 кг

^{3/4 т = 1 т : 4 • 3 = 1000 : кг 4 • 3 = 750 кг}

Сторінка 86

Завдання 2

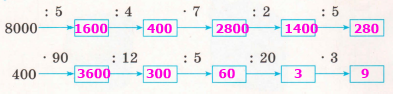
^{8000 : 5 = (5000 + 3000) : 5 = 1000 + 600 = 1600 1600 : 4 = 16 сот. : 4 = 4 сот. = 400}

^{400 • 7 = 4 сот. • 7 = 28 сот. = 2800 2800 : 2 = 28 сот. : 2 = 14 сот. = 1400 1400 : 5 = (1000 + 400) : 5 = 200 + 80 = 280}

^{400 • 90 = 3600 3600 : 12 = 3600 : (6 • 2) = 3600 : 6 : 2 = 600 : 2 = 300}

^{300 : 5 = 30 дес. : 5 = 6 дес. = 60 60 : 20 = 6 : 2 = 3 3 • З = 9}

Завдання 3

77 880 : 55 = 1416

29 736 : 56 = 531

_77880| 55

55 1416

_228

220

_88

_330

330

х 1416

+ 7080

7080

77880

_29736| 56

280 531

_173

168

_56

х 531

+3186

2655

29736

Завдання 4

На двох ділянках, площею 6 га і 10 га, посіяли 1920 кг насіння льону. Скільки кілограмів насіння льону було посіяно на кожній ділянці, якщо норми висіву однакові?

^{Ділянка}	^{Маса на 1 га (норма висіву)}	^{Кількість гектарів}	^{Загальна маса насіння}
^І	^{однаково}	⁶	^?	^{1920 кг}
^ІІ	^{однаково}	¹⁰	^?	^{1920 кг}
^Разом	^?	^?		^{1920 кг}