© Барна Р., 2021
Серія "Вчимось разом" до підручника
"Математика 4 клас Скворцова С., Онопрієнко О."
Сторінка 47
Завдання 1 Ділення з остачею
Групи часток: частка дорівнює 0, частка не дорівнює нулю.
43 : 8 = 5 (ост. 3) перевірка 5 • 8 + 3 = 40 + 3 = 43
7 : 9 = 0 (ост. 7) перевірка 0 • 9 + 7 = 0 + 7 = 7
65 : 10 = 6 (ост. 5) перевірка 6 • 10 + 5 = 60 + 5 = 65
32 : 45 = 0 (ост. 32) перевірка 0 • 45 + 32 = 0 + 32 = 32
Завдання 2
|
_732 | 3 6 244 _13 12 _12 12 0 |
_132 | 3 12 44 _12 12 0 |
Завдання 3 Ділення перевіряємо множенням
|
_868 | 7 7 124 _16 14 _28 28 0 |
х124 7 868 |
_315 | 9 27 35 _45 45 0 |
х35 9 315 |
_522 | 6 48 87 _42 42 0 |
х87 6 522 |
_992 | 4 8 248 _19 16 _32 32 0 |
х248 4 992 |
Сторінка 48
Завдання 4 Письмове множення
|
Письмове множення |
х198 5 990 |
х96 7 672 |
х332 3 996 |
х87 6 522 |
х476 2 952 |
|
Перевірка письмовим діленням |
_990 | 5 5 198 _49 45 _40 40 0 |
_672 | 7 63 96 _42 42 0
|
_996 | 3 9 332 _9 9 _6 6 0 |
_522 | 6 48 87 _42 42 0 |
_952 | 2 8 476 _15 14 _12 12 0 |
Завдання 5 Порівняння чисел
|
561 – (651 : 3 + 195) > 144 : 3 • 7 – 248 |
|
|
561 – (651 : 3 + 195) = 149 1) 651 : 3 = (600 + 30 + 21) : 3 = 200 + 10 + 7 = 217 2) 217 + 195 = 217 + 200 – 5 = 417 – 5 = 412 3) 561 – 412 = 141 + (420 – 412) = 141 + 8 = 149 |
144 : 3 • 7 – 248 = 88 1) 144 : 3 = (120 + 24) : 3 = 120 : 3 + 24 : 3 = 40 + 8 = 48 2) 48 • 7 = (40 + 8) • 7 = 280 + 56 = 336 3) 336 – 248 = 336 – 300 + 52 = 36 + 52 = 88 |
|
(603 – 918 : 6) : 5 = 427 – (248 : 4 + 275) |
|
|
(603 – 918 : 6) : 5 = 90 1) 918 : 6 = (600 + 300 + 18) : 6 = 100 + 50 + 3 = 153 2) 603 – 153 = 603 – 200 + 47 = 403 + 47 = 450 3) 450 : 5 = 90 |
427 – (248 : 4 + 275) = 90 1) 248 : 4 = (240 + 8) : 4 = 60 + 2 = 62 2) 62 + 275 = 200 + 130 + 7 = 337 3) 427 – 337 = 427 – 327 – 10 = 100 – 10 = 90 |
Завдання 6 Вирази
Якщо k = 3, тоді (459 : k + 35 • k) : 2 = (459 : 3 + 35 • 3) : 2 = (153 + 105) : 2 = 258 : 2 = (200 + 40 + 18) : 2 = 100 + 20 + 9 = 129
Якщо k = 9, тоді (459 : k + 35 • k) : 2 = (459 : 9 + 35 • 9) : 2 = (51 + 315) : 2 = 366 : 2 = (200 + 160 + 6) : 2 = 100 + 80 + 3 = 183
Якщо k = 3, тоді (375 + 624) : k + 68 • k = 999 : k + 68 • k = 999 : 3 + 68 • 3 = 333 + 204 = 537
Якщо k = 9, тоді (375 + 624) : k + 68 • k = 999 : k + 68 • k = 999 : 9 + 68 • 9 = 111 + 612 = 723
Завдання 7 Складена задача на знаходження частини числа
У бочці назбиралося 150 л дощової води, а потім у бочку долили третину від кількості води, що в ній була. На полив витратили половину всієї води. Скільки літрів води залишилось?
Короткий запис
Було — 150 л
Долили — ?, 1/3 від 150 л
Стало (Було) — ?
Витратили — ?, 1/2 від було
Залишилось — стільки ж
Схема
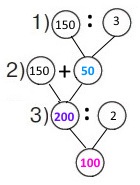
Вираз (150 + 150 : 3) : 2
Розв’язання
1) 150 : 3 = 50 (л) – літрів води долили.
2) 150 + 50 = 200 (л) – літрів води стало в бочці.
Якщо витратили половину, тоді залишилася інша половина, тому
3) 200 : 2 = 100 (л) – літрів води залишилося.
Відповідь: залишилося 100 літрів води.
Завдання 8 Задача на знаходження цілого за його частиною
На береговому схилі Чорного моря квітникарі висаджували тюльпани. Половину всіх цибулин посадили на клумбі, після чого залишилося 48 цибулин. Скільки цибулин було у квітникарів?
Короткий запис
1 — ? цибулин
1/2 — 48 цибулин
Розв’язання
Якщо половину всіх висадили, тоді залишилася інша половина, тобто 48 цибулин — це 1/2 від було, тому
48 • 2 = 48 + 48 = 96 (ц.) – цибулин тюльпанів висадили на клумбі.
Відповідь: на клумбі висадили 96 цибулин тюльпанів.
Завдання 9 Обчисли периметр прямокутника зі сторонами 3 см і 2 см.
Розв’язання
Р = (3 + 2) • 2 = 5 • 2 = 10 (см) – периметр прямокутника зі сторонами 3 см і 2 см.
2 спосіб
Р = 3 • 2 + 2 • 2 = 6 + 4 = 10 (см) – периметр прямокутника зі сторонами 3 см і 2 см.
3 спосіб
Р = 3 + 2 + 3 + 2 = 10 (см) – периметр прямокутника зі сторонами 3 см і 2 см.
Відповідь: периметр прямокутника 10 см.
Сторінка 49
Завдання 1 Множення і ділення на розрядну одиницю
60 : 10 = 6 27 • 10 = 270 710 : 10 = 71 8 • 100 = 800 400 : 100 = 4
Завдання 2 Взаємозв'язок дій множення і ділення
Спосіб послідовного ділення: 560 : 70 = 560 : (10 • 7) = 560 : 10 : 7 = 56 : 7 = 8
Спосіб послідовного множення: 6 • 140 = 6 • (14 • 10) = (6 • 14) • 10 = 84 • 10 = 840
Спосіб укрупнення розрядних одиниць:
560 : 70 = 56 дес. : 7 дес. = 8
6 • 140 = 6 • 14 дес. = 84 дес. = 840
Завдання 3
|
Вираз |
856 : 8 |
216 : 3 |
168 : 8 |
|
Перше неповне ділене |
8 |
21 |
16 |
|
3 |
2 |
2 |
|
|
Рівність хибна, бо не сходиться кількість у частці |
856 : 8 ≠ 17 |
216 : 3 ≠ 102 |
168 : 8 ≠ 122 |
Завдання 4
|
_234 | 3 21 78 _24 24 0 |
_736 | 8 72 92 _16 16 0 |
_828 | 4 8 207 _28 28 0 |
_981 | 3 9 327 _8 6 _21 21 0 |
_342 | 9 27 38 _72 72 0 |
|
|
Перевірка множенням |
х78 3 234 |
х92 8 736 |
х207 4 828 |
х327 3 981 |
х38 9 342 |
Сторінка 50
Завдання 5
|
Ділення |
х84 7 588 |
х186 4 744 |
х247 4 988 |
х73 9 657 |
х321 3 963 |
|
Перевірка письмовим діленням |
_588 | 7 56 84 _28 28 0 |
_744 | 4 4 186 _34 32 _24 24 0 |
_988 | 4 8 247 _18 16 _28 28 0 |
_657 | 9 63 73 _27 27 0 |
_963 | 3 9 321 _6 6 _3 3 0 |
Завдання 6 Задачу на зведення до одиниці можна розв’язати тільки способом відношень
Юрко пофарбував 12 рамок для картин, фарбуючи щогодини 5 рамок. Скільки рамок має фарбувати Юрко щогодини, щоб за той самий час пофарбувати 24 рамки?
|
1 спосіб (відношень) Короткий запис 5 рамок — 12 рамок ? рамок — 24 рамки Вираз 5 • (24 : 12) План розв’язування 1) У скільки разів більша загальна кількість рамок? 2) Скільки рамок має фарбувати щогодини? Розв’язання 1) 24 : 12 = 24 : 6 : 2 = 2 (рази) – у стільки разів більша загальна кількість рамок. 2) 5 • 2 = 10 (р.) – рамок має фарбувати щогодини. |
2 спосіб (рівняння для відношень) Короткий запис 5 рамок — 12 рамок х рамок — 24 рамки Нехай х (р.) – рамок має фарбувати щогодини, тоді 24 : 12 (разів) – у стільки разів більша загальна кількість рамок, а також 5 : х (разів) – у стільки разів більше має пофарбувати рамок, тому складемо рівняння х : 5 = 24 : 12 х : 5 = 2 х = 2 • 5 = 10 (р.) – рамок має фарбувати щогодини. |
Відповідь: щогодини має фарбувати 10 рамок.
Завдання 7 Порядок дій
|
(458 : 2 + 804 : 3) • 2 – 658 = 336 |
(816 : 8 – 369 : 9 + 401) : 3 = 154 |
||||||||
|
_458 | 2 4 229 _5 4 _18 18 0 |
_804 | 3 6 268 _20 18 _24 24 0 |
+229 268 497 |
х497 2 994 |
_994 658 336 |
_816 | 8 8 102 _16 16 0 |
_369 | 9 36 41 _9 9 0 |
_102 41 61 |
+401 61 462 |
_462 | 3 3 154 _16 15 _12 12 0 |
Завдання 8 Рівняння
|
8 • с = 356 – 284 8 • с = 72 с = 72 : 8 с = 9 8 • 9 = 72 356 – 284 = 72 72 = 72 |
915 : 3 + b = 835 305 + b = 835 b = 835 – 305 b = 530 915 : 3 + 530 = 835 835 = 835 |
k : 3 – 179 = 203 : 7 k : 3 – 179 = 29 k : 3 = 29 + 179 k : 3 = 208 k = 208 • 3 k = 624 624 : 3 – 179 = 29 203 : 7 = 29 29 = 29 |
Завдання 9 Складена задача на збільшення на частину числа
Довжина відрізка АВ — 64 мм. Накресли відрізок СК, довжина якого більша за довжину відрізка АВ на чверть.
Короткий запис
АВ — 64 мм
СК — ?, на ? (1/4 від АВ) більше
1) 64 : 4 = (40 + 24) : 4 = 16 (мм) – чверть відрізка АВ.
2) 64 + 16 = 80 (мм) = 8 (см) – довжина відрізка СК.
Завдання 10 Сім'я придбала туристичну путівку на 9 днів. Перший день відпочинку припадає на 29 жовтня. На який день тижня припадає останній день відпочинку?
Міркуємо так. Якщо 29 жовтня 2022 року випадає субота, оскільки у тижні 7 днів, тому субота припаде на 8 день путівки, а останнім днем відпочинку буде неділя.
Відповідь: неділя.
Завдання 11 Художниці Юлія й Оксана та художник Володимир оформили 9 банерів. Юлія оформила на третину більше банерів, ніж Оксана, а Володимир — на третину менше, ніж Оксана. Скільки банерів оформила кожна особа?
Міркуємо так. Якщо Володимир оформив на третину банерів менше, ніж Оксана, то це означає різницю між усіма частинами Оксани і Володимира, тобто 3 = 4 – 1. Тобто Оксана оформила 4 банери, а Володимир – 1 банер (третина). Якщо Юля оформила на третину банерів більше, то вона оформила, 5 банерів.
Відповідь: Оксана оформила 4 банери, Володимир – 2 банери, а Юля – 5 банерів.
Завдання 12
|
х*3* 3 7*8 |
х236 3 708 |
х*** 7 672 |
х 96 7 672 |
х*8* 4 7*0 |
х180 4 720 |
|
18 : 3 = 6 3 • 3 + 1 = 10 + 0 (7 – 1) : 3 = 2 |
42 : 7 = 6 (67 – 4) : 7 = 9
|
4 • 0 = 0 8 • 4 = 32 = 30 + 2 (7 – 3) : 4 = 1 |
|||
Сторінка 51
Завдання 1
42 • 10 = 420 400 : 100 = 4 9 • 100 = 900 300 : 10 = 30
700 : 100 = 7 7 • 10 = 70 1000 : 10 = 100 3 • 100 = 300
Завдання 2
|
32 : 10 = 3 (ост. 2) |
834 : 100 = 8 (ос. 34) |
420 : 100 = 4 (ост. 20) |
563 : 10 = 56 (ост. 3) |
Завдання 3
Прийом послідовного множення (або ділення):
960 : 80 = 960 : (10 • 8) = 960 : 10 : 8 = 96 : 8 = (80 + 16) : 8 = 12
3 • 260 = 3 • (26 • 10) = 3 • 26 • 10 = 3 • (20 + 6) • 10 = 78 • 10 = 780
800 : 160 = 800 : (10 • 16) = 800 : 10 : 16 = 80 : 16 = 5
23 • 40 = 23 • (4 • 10) = 23 • 4 • 10 = (20 + 3) • 4 • 10 = 92 • 10 = 920
Прийом укрупнення розрядних одиниць:
960 : 80 = 96 дес. : 8 дес. = 12
3 • 260 = 3 • 26 дес. = 3 • (20 дес. + 6 дес.) = 78 дес. = 780
800 : 160 = 80 дес. : 16 дес. = 5
23 • 40 = 23 • 4 дес. = (20 + 3) • 4 дес. = 92 дес. = 920
Завдання 4, 5
|
х186 5 930 |
х96 7 672 |
х176 3 528 |
х76 6 456 |
х32 3 96 |
х320 30 960 |
Сторінка 52
Завдання 6
|
Письмове множення |
х17 40 680 |
х29 30 870 |
х33 30 990 |
х48 20 960 |
х46 20 920 |
|
х23 40 920 |
х18 50 900 |
х22 40 880 |
х25 40 1000 |
х31 30 930 |
|
|
Перевірка письмовим діленням |
_680 | 40 400 17 _280 280 0 |
_870 | 30 600 29 _270 270 0 |
_990 | 30 90 33 _90 90 0 |
_960 | 20 80 48 _160 160 0 |
_920 | 20 80 46 _120 120 0 |
|
_920 | 40 80 23 _120 120 0 |
_900 | 50 50 18 _400 400 0 |
_880 | 40 800 22 _800 800 0 |
_1000 | 40 80 25 _200 200 0 |
_930 | 30 900 31 _30 30 1 |
Завдання 7
Використали прийом послідовного ділення, розподілений закон ділення відносно додавання:
|
900 : 30 = 900 : 10 : 3 = 90 : 3 = 30 980 : 70 = 980 : 10 : 7 = 98 : 7 = (70 + 28) : 7 = 14 960 : 30 = 960 : 10 : 3 = 96 : 3 = 32 680 : 40 = 680 : 10 : 4 = 68 : 4 = (40 + 28) : 4 = 17 |
780 : 30 = 780 : 10 : 3 = 78 : 3 = (60 + 18) : 3 = 26 800 : 20 = 800 : 10 : 2 = 80 : 2 = 40 990 : 90 = 990 : 10 : 9 = 99 : 9 = 11 780 : 60 = 780 : 10 : 6 = 78 : 6 = (60 + 18) : 6 = 13 960 : 80 = 960 : 10 : 8 = 96 : 8 = (80 + 16) : 8 = 12 880 : 40 = 880 : 10 : 4 = 88 : 4 = 22 |
Сторінка 53
Завдання 1
|
(540 : 180) • (720 : 36) • (900 : 180) : 100 • (148 : 37) = 12 (980 : 7) : (840 : 120) • (84 : 28) • (154 : 22) : (650 : 130) = 84 |
|
|
1) 540 : 180 = 540 : 10 : 9 : 2 = 54 : 9 : 2 = 6 : 2 = 3 2) 720 : 36 = 20 3) 900 : 180 = 900 : 90 : 2 = 10 : 2 = 5 4) 148 : 37 = 4 5) 3 • 20 = 60 6) 60 • 5 = 300 7) 300 : 100 = 3 8) 3 • 4 = 12 |
1) 980 : 7 = (700 + 280) : 7 = 140 2) 840 : 120 = 840 : 10 : 12 = 84 : 12 = 7 3) 84 : 28 = 3 4) 154 : 22 = 154 : 2 : 11 = 77 : 11 = 7 5) 650 : 130 = 65 : 13 = 5 6) 140 : 7 = 20 7) 20 • 3 = 60 8) 60 • 7 = 420 9) 420 : 5 = (400 + 20) : 5 = 84 |
Завдання 2 У двох останніх випадках доцільно переставити множники:
|
Множення |
х49 20 980 |
х32 30 960 |
х18 50 900 |
х290 3 870 |
х150 6 900 |
|
Перевірка діленням |
_980 | 2 8 49 _18 18 0 |
_960 | 30 900 32 _60 60 0 |
_900 | 50 50 18 _400 400 0 |
_870 | 3 6 290 _27 27 0 |
_900| 6 6 150 _30 30 0 |
Завдання 3, 4
|
Ділення |
_920 | 40 800 23 _120 120 0 |
_840 | 60 60 14 _240 240 0 |
_510 | 30 300 17 _210 210 0 |
_990 | 30 90 33 _90 90 0 |
_960 | 60 60 16 _360 360 0 |
|
_950 | 50 50 19 _450 450 0 |
_480 | 30 30 16 _180 180 0 |
_720 | 40 40 18 _320 320 0 |
_910 | 70 70 13 _210 210 0 |
_860 | 20 80 43 _60 60 0 |
|
|
Перевірка множенням
|
х23 40 920 |
х14 60 840 |
х17 30 510 |
х33 30 990 |
х16 60 960 |
|
х19 50 950 |
х16 30 480 |
х18 40 720 |
х13 70 910 |
х43 20 860 |
Завдання 5
1) (567 – 328 + 481) : 40 + (508 – 329) = 197
2) 720 : (563 + 248 – 751) • 80 = 960
3) 960 : 4 • 2 : 60 • 90 – 89 = 631
4) 224 : 7 • 30 – 720 : 40 • 7 = 834
|
_567 328 239 |
+239 481 720 |
_508 329 179 |
_720 | 40 40 18 _320 320 0 |
+179 18 197 |
|
+563 248 811 |
_811 751 60 |
_720 | 60 60 12 _120 120 0 |
х12 80 960 |
|
|
_960 | 4 8 240 _16 16 0 |
х240 2 480 |
480 : 60 = 480 : 10 : 6 = 48 : 6 = 8 8 • 90 = 720 720 – 89 = 720 – 100 + 11 = 620 + 11 = 631
|
||
|
_224 | 7 21 32 _14 14 0 |
х32 30 960 |
_720 | 40 40 18 _320 320 0 |
х18 7 126 |
_960 126 834 |
Завдання 6 Довели переставний закон додавання
Для обчислень використали розподільний закон множення відносно додавання:
36 • 24 = 36 • (20 + 4) = 36 • 20 + 36 • 4 = 720 + 144 = 864
27 • 32 = 27 • (30 + 2) = 27 • 30 + 27 • 2 = 810 + 54 = 864