Інші завдання дивись тут...

СТОРІНКА 4

Завдання 1

Лічимо від 95 до 108:

95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108

"Дев'яносто п'ять, дев'яносто шість, дев'яносто сім, дев'яносто вісім, дев'яносто дев'ять, сто, сто один, сто два, сто три, сто чотири, сто п'ять, сто шість, сто сім, сто вісім!".

 

Завдання 2  

6 сот. 4 дес. 8 од. = 648 – шістсот сорок вісім;

3 сот. 2 дес. 1 од. = 321 – триста двадцять один;

9 сот. 4 дес. 8 од. = 948 – дев'ятсот сорок вісім;

1 сот. 2 дес. 3 од. = 123 – сто двадцять три.

 

Завдання 3 Групування розрядів у класи 

80 – вісімдесят, 8 дес.

26 – двадцять шість, 2 дес. 6 од.

430 – чотириста тридцять, 4 сот. 3 дес.

709 – сімсот дев’ять, 7 сот. 9 од.

400 – чотириста, 4 сот.

356 – триста п’ятдесят шість, 3 сот. 5 деc. 6 од.

864 – вісімсот шістдесят чотири, 8 сот. 6 дес. 4 од.

1000 – тисяча, 1 тис.

 

Завдання 4  Сума розрядних доданків

Артем виконав завдання равильно

 

Завдання 5

800 + 30 + 7 = 83 900 + 6 = 906 400 + 20 = 420

8 • 100 + 3 • 10 + 7 = 83 9 • 100 + 6 = 906 4 • 100 + 2 • 10 = 420

Завдання 6 «Сусіди» числа

562:   561 і 563        562 – 1 = 561    562 + 1 = 563

200:   199 і 201        200 – 1 = 199    200 + 1 = 201   

754:   753 і 755        754 – 1 = 753    754 + 1 = 755

931:   930 і 932        931 – 1 = 930    931 + 1 = 932

У натуральному ряді наступне число на одиницю більше за попереднє.

У натуральному ряді попереднє число на одиницю менше від наступного.

Щоб одержати число з наступного до нього числа, треба відняти одиницю.

Щоб одержати число з попереднього до нього числа, треба додати одиницю.

Одержати число іншим способом не можна.

 

СТОРІНКА 5

Завдання 7  Характеристика чисел 867, 178, 805

Число	867	178	805
«Сусіди»	866, 868	177, 179	804, 806
Розрядні доданки	800 + 60 + 7	100 + 70 + 8	800 + 5
Розрядний склад	8 сот. 6 дес. 7 од.	1 сот. 7 дес. 8 од.	8 сот. 5 од.

Характеристика чисел 438, 500, 14

Число	438	500	14
«Сусіди»	437, 439	499, 501	13, 15
Розрядні доданки	400 + 30 + 8	500	10 + 4
Розрядний склад	4 сот. 3 дес. 8 од.	5 сот.	1 дес. 4 од.

Завдання 8

Із цифр 2, 7, 8 склали можливі трицифрові числа так, щоб цифри в записі числа не повторювалися. Скільки таких чисел можна скласти? Шість

 

278 двісті сімдесят вісім	728 сімсот двадцять вісім	827 вісімсот двадцять сім
287 двісті вісімдесят сім	782 сімсот вісімдесят два	872 вісімсот сімдесят два

Завдання 9 Записали можливі трицифрові числа за допомогою цифр 4, 6, 9 так, щоб цифри в записі кожного числа не повторювалися.

Утворено 6 чисел (469, 496, 649, 694, 946, 964)

Парних 4 числа  (496, 694, 946, 964)

Непарних 2 числа (469,649)

 

Завдання 10

800 – 1 = 799        500 + 200 = 700      356 – 6 = 350

300 + 8 = 308        456 – 400 = 56        899 + 1 = 900

800 + 10 + 8 = 818   500 + 40 = 540     900 + 5 = 905    672 – 70 = 602

 

СТОРІНКА 6

Завдання 1  Додавання частинами

Сполучний закон додаванння а + (b + с) = (а + b) + с

67 + 25 = 67 + (20 + 5) = (67 + 20) + 5 = 87 + 5 = 92

67 + 25 = 67 + (3 + 22) = (67 + 3) + 22 = 70 + 22 = 92

 

Завдання 2 Множення чисел

Сполучний закон множення а • (b • с) = (а • b) • с 

Розподільний закон множення відносно додавання а • (b + с) = а • с + b • с

6 • 12 = 12 • 6 = 12 + 12 + 12 + 12 + 12 + 12 = 72

6 • 12 = 6 • (10 + 2) = 6 • 10 + 6 • 2 = 60 + 12 = 72

6 • 12 = 6 • (6 • 2) = (6 • 6) • 2 = 36 • 2 = 72

 

Завдання 3 Ділення чисел

Послідовне ділення а : (b • с) = (а : b) : с 

Розподільний закон ділення відносно додавання (а + b) : с = а : с + b : с, якщо а і b діляться на с націло, с≠0

48 : 16 = 3,  тому 3 • 16 = 48

48 : 16 = 48 : (8 • 2) = (48 : 8) : 2 = 6 : 2 = 3

48 : 16 = 48 : (4 • 4) = (48 : 4) : 4 = 12 : 4 = 3

 

СТОРІНКА 7

Завдання 4

14 + 14 + 14 + 14 = 14 • 4 = (10 + 4) • 4 = 10 • 4 + 4 • 4 = 40 + 16 = 56

(75 + 18) – 25 = (75 – 25) + 18 = 50 + 18 = 68

(2 • 23) • 5 = (2 • 5) • 23 = 10 • 23 = 230

(18 • 5) • 4 = (5 • 4) • 18 = 20 • 18 = (10 + 8) • 20 = 10 • 20 + 8 • 20 = 200 + 160 = 360

480 + (356 + 20) = (480 + 20) + 356 = 500 + 356 = 856

(234 + 567) + 66 = (234 + 66) + 567 = 300 + 567 = 867

 

Завдання 5

37 • 4 = (30 + 7) • 4 = 30 • 4 + 7 • 4 = 120 + 28 = 148

96 : 16 = 6, бо 16 • 6 = (10 + 6) • 6 = 60 + 36 = 96

38 • 4 = (30 + 8) • 4 = 30 • 4 + 8 • 4 = 120 + 32 = 152

80 : 16 = 80 : (8 • 2) = 80 : 8 : 2 = 10 : 2 = 5

90 : 18 = 90 : (9 • 2) = 90 : 9 : 2 = 10 : 2 = 5

42 : 3 = (30 + 12) : 3 = 30 : 3 + 12 : 3 = 10 + 4 = 14

6 • 27 = (20 + 7) • 6 = 20 • 6 + 7 • 6 = 120 + 42 = 162

70 : 14 = 70 : (7 • 2) = 70 : 7 : 2 = 10 : 2 = 5

19 • 7 = (10 + 9) • 7 = 10 • 7 + 9 • 7 = 70 + 63 = 70 + 30 + 33 = 133

91 : 13 = 7, бо 13 • 7 = (10 + 3) • 7 = 70 + 21 = 91

60 : 5 = (50 + 10) : 5 = 50 : 5 + 10 : 5 = 10 + 2 = 12

92 : 23 = 4, бо 23 • 4 = (20 + 3) • 4 = 80 + 12 = 92

76 : 4 = (40 + 36) : 4 = 40 : 4 + 36 : 4 = 10 + 9 = 19

18 • 6 = (10 + 8) • 6 = 10 • 6 + 8 • 6 = 60 + 48 = 108

153 : 9 = (90 + 63) : 9 = 90 : 9 + 63 : 9 = 10 + 7 = 17

112 : 16 = 7, бо 16 • 7 = (10 + 6) • 7 = 70 + 42 = 70 + 30 + 12 = 112

 

Завдання 6 Множення на число 9 

а • 11 = а • 10 + а а • 101 = а • 100 + а

а • 9 = а • 10 – а а • 99 = а • 100 – а

28 • 9 = 28 • 10 – 28 = 280 – 28 = 250 + (30 – 28) = 250 + 2 = 252

7 • 101 = 7 • 100 + 7 = 700 + 7 = 707

32 • 11 = 32 • 10 + 32 = 320 + 32 = 352

7 • 99 = 7 • 100 – 7 = 700 – 7 = 693

3 • 99 = 3 • 100 – 3 = 300 – 3 = 297

16 • 11 = 16 • 10 + 16 = 160 + 16 = 176

8 • 101 = 8 • 100 + 8 = 800 + 8 = 808

32 • 9 = 32 • 10 – 32 = 320 – 32 = 280 + (40 – 32) = 280 + 8 = 288

 

Завдання 7

До магазину привезли 7 ящиків яблук, по 12 кг у кожно­му ящику, і 6 ящиків груш, по 15 кг у кожному ящику.

12 • 7 (кг) – маса яблук;

15 • 6 (кг) – маса груш;

12 • 7 + 15 • 6 (кг) – маса фруктів (яблук і груш разом)

15 • 6 – 12 • 7 (кг) – на стільки більша маса груш, ніж яблук

 

Завдання 8

У двох коробках лежали горіхи, порівну в кожній. Із другої коробки в першу переклали один горіх. На скільки більше горіхів стало в першій коробці? 

Міркуємо так. Якщо з другої коробки забрали горіх, то в першій коробці стало на 1 горіх більше, Потім цей горіх переклали в першу коробку, тоді в цій коробці стане уже на 2 горіхи більше. 

 

СТОРІНКА 8

Завдання 1

Значення першого виразу в стовпчику обчислити легше.

7 + 3 = 10          

7 + 9 = 7 + (3 + 6) = (7 + 3) + 6 = 10 + 6 = 16

Доданок на 6 більший й, відповідно, сума на 6 більша.

10 – 8 = 2         

16 – 8 = (10 + 6) – 8 = (10 – 8) + 6 = 2 + 6 = 8

Зменшуване на 6 більше й, відповідно, різниця на 6 більша.

13 – 3 = 10        

13 – 9 = 13 – (6 + 3) = (13 – 3) – 6 = 10 – 6 = 4

Від'ємник на 6 більший й, відповідно, різниця на 6 менша.

7 • 8 = 56          

7 • 16 = 7 • 8 • 2 = 56 • 2 = 56 + 56 = 112

Множник удвічі більший й, відповідно, добуток удвічі більший.

18 : 3 = 6          

36 : 3 = (18 • 2) : 3 = 18 : 3 • 2 = 6 • 2 = 12

Ділене удвічі більше й, відповідно, частка удвічі більша.

48 : 8 = 6          

48 : 16 = 48 : (8 • 2) = 48 : 8 : 2 = 6 : 2 = 3

Дільник удвічі більший й, відповідно, частка удвічі менша.

 

Завдання 2

1) Значення суми чисел 145 і 276, якщо

перший доданок збільшити на 30, також збільшиться на 30.

(145 + 30) + 276 = (145 + 276) + 30

Значення суми чисел 145 і 276, якщо

другий доданок зменшити на 45, також зменшиться на 45.

145 + (276 – 45) = (145 + 276) – 45  

2) Значення різниці чисел 800 і 545, якщо

зменшуване змен­шити на 40, також зменшиться на 40.

(800 – 40) – 545 = (800 – 545) – 40

Значення різниці чисел 800 і 545, якщо

від'ємник збільшити на 20 і зменшити на 20, не зміниться. 

800 – (545 + 20 – 20) = 800 – 545

3) Значення добутку чисел 36 і 10, якщо

перший множник зменшити у 2 рази, збільшити у 2 рази, не зміниться.

(36 : 2 • 2) • 10 = 36 • 10

Значення добутку чисел 36 і 10, якщо

другий множник збільшити в 4 рази і зменшити в 5 разів, збільшиться в 4/5.

(36 : 5 • 4) • 10 = 36 • 4/5 • 10 = 36 • 10 • 4/5

4) Значення частки чисел 108 і 18, якщо

ділене збільшити у 2 рази, зменшити в 4 рази, зменшиться у 2 рази.

108 : 18 = 6        (108 • 2 : 4) : 18 = 3        6 : 3 = 2

Значення частки чисел 108 і 18, якщо

дільник зменшити в 6 разів, збільшити у 2 рази, збільшиться у 3 рази.

108 : 18 = 6       108 : (18 : 6 • 2) = 108 : 6 = 18     18 : 6 = 3

 

Завдання 3 Застосовані правила

54 + 28 = 54 + 30 – 2 = 84 – 2 = 82 Додавання способом округлення

84 – 38 = 84 – 40 + 2 = 44 + 2 = 46 Віднімання способом округлення

36 • 5 = 36 • 10 : 2 = 360 : 2 = 180 Множення числа на 5: можна число помножити на 10, а отриманий добуток поділити на 2.

740 : 5 = 740 : 10 • 2 = 74 • 2 = 148 Ділення числа на 5: можна число поділити на 10, а отриману частку помножити на 2.

8 • 25 = 8 • 100 : 4 = 800 : 4 = 200 Множення числа на 25: можна число помножити на 100, а отриманий добуток поділити на 4.

300 : 25 = 300 : 100 • 4 = 3 • 4 = 12 Ділення числа на 25: можна число поділити на 100, а отриману частку помножити на 4.

 

СТОРІНКА 9

Завдання 4

38 + 24 = 40 + 24 – 2 = 64 – 2 = 62

23 • 5 = 23 • 10 : 2 = 230 : 2 = 115

720 : 3 = (600 + 120) : 3 = 600 : 3 + 120 : 3 = 200 + 40 = 240

81 – 56 = 81 – 60 + 4 = 21 + 4 = 25

460 : 5 = 460 : 10 • 2 = 46 • 2 = 92

300 : 25 = 300 : 100 • 4 = 3 • 4 = 12

34 + 19 = 34 + 20 – 1 = 54 – 1 = 53

7 • 25 = 7 • 100 : 4 = 700 : 4 = 175

64 – 46 = 64 – (50 – 4) =  64 – 50 + 4 = 14 + 4 = 18

300 : 50 = 30 : 5 = 6

 

Завдання 5

1) Довжина відрізка • Кількість відрізків = Загальна довжина

3 • 2 = 6 (м) — загальна довжина двох відрізів по 3 м кожний;

6 • 2 = 12 (м) — загальна довжина двох відрізів по 6 м кижний;

12 : 6 = 2 (р.) — залежність загальної довжини.

Якщо довжину відрізка збільшити у 2 рази, загальна довжина також збільшиться у 2 рази.

2) Місткість 1 посудини • Кількість посудин = Загальна місткість

4 • 2 = 8 (л) — загальна місткість двох посудин по 4 л кожна;

4 • 6 = 24 (л) — місткість другої шести посудин по 6 л кожна.

24 : 8 = 3 (р.) — залежність загальної місткості.

Якщо кількість посудин збільшити у 3 рази, загальна місткість також збільшиться у 3 рази.

 

Завдання 6

Проста задача на множення Купили персиків 4 ящики, по 12 кілограмів у кожному. Яка загальна маса персиків? Маса 1 ящ. (кг) Кількість ящ. (шт.) Загальна маса (кг) 12 4   Розв’язання 12 • 4 = 48 (кг) Відповідь: загальна маса персиків 48 кілограмів.
Перша обернена задача. Купили 48 кг персиків у ящиках, по 12 кілограмів в кожному. Скільки було ящиків?  Маса 1 ящ. (кг) Кількість ящ. (шт.) Загальна маса (кг) 12 ? 48 Розв’язання 48 : 12 = 4 (ящ.) Відповідь: було 4 ящики.	Друга обернена задача Купили 48 кг персиків у ящиках, порівно в кожному. Ящиків було 4. Скільки кілограмів персиків у кожному ящику?  Маса 1 ящ. (кг) Кількість ящ. (шт.) Загальна маса (кг) ? 4 48 Розв’язання 48 : 4 = 12 (кг) Відповідь: у кожному ящику 12 кілограмів персиків.

Завдання 7 

38 + 16 = 38 + 20 – 4 = 54 71 – 47 = 71 – 50 + 3 = 24 42 • 5 = 42 • 10 : 2 = 210

108 – 76 = 108 – 80 + 4 = 32 700 : 50 = 700 : 100 • 2 = 14 6 • 25 = 6 • 100 : 4 = 150

Завдання 8

Накресли квадрат, периметр якого дорівнює 20 см. Накресли інший прямокутник із таким периметром.

20 : 4 = 5 (см) – сторона квадрата

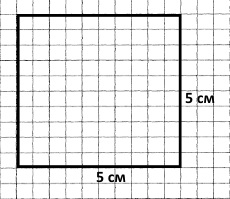
20 : 2 = 10 (см) – півпериметр (сума довжини і ширини)

Сторони прямокутника можуть бути такими:

9 см і 1 см, 8 см і 2 см, 7 см і 3 см, 6 см і 4 см.

СТОРІНКА 10

Завдання 2

1) 46 – 23 = (46 – 20) – 3 = 26 – 3 = 23

    346 – 23 = (300 + 46) – 23 = 300 + (46 – 23) = 300 + 23 = 323

    346 – 123 = (300 – 100) + (46 – 23) = 200 + 23 = 223

2) 35 + 22 = (35 + 20) + 2 = 55 + 2 = 57

    435 + 22 = 400 + (35 + 22) = 400 + 57 = 457

    435 + 322 = (400 + 300) + (35 + 22) = 700 + 57 = 757

3) 64 – 26 = (64 – 24) – 2 = 40 – 2 = 38

    264 – 26 = (200 + 64) – 26 = 200 + (64 – 26) = 200 + 38 = 238

    264 – 126 = (200 – 100) + (64 – 26) = 100 + 38 = 138

4) 45 + 27 = 45 + 5 + 22 = 50 + 22 = 72

    345 + 27 = 300 + (45 + 27) = 300 + 72 = 372

    345 + 127 = (300 + 100) + (45 + 27) = 400 + 72 = 472

 

Завдання 3

1) 35 + 23 = (30 + 20) + (5 + 3) = 50 + 8 = 58

    135 + 223 = (100 + 200) + (30 + 20) + (5 + 3) = 300 + 50 + 8 = 358

2) 67 – 43 = (60 – 40) + (7 – 3) = 24

    467 – 243 = (400 – 200) + (60 – 40) + (7 – 3) = 200 + 20 + 4 = 224

3)  37 + 18 = (30 + 10) + (7 + 8) = 40 + 15 = 55

     237 + 118 = (200 + 100) + (30 + 10) + (7 + 8) = 300 + 40 + 15 = 355

4) 82 – 45 = (70 – 40) + (12 – 5) = 30 + 7 = 37

    482 – 145 = (400 – 100) + (70 – 40) + (12 – 5) = 300 + 30 + 7 = 337

Інші завдання дивись тут...