Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 10 Властивість паралельних прямих
Завдання 212 На малюнку 10.6 a || b, c – січна.
1) Кути 5 і 4; 2 і 7 є відповідними при перетині паралельних прямих січною, тому рівними (теорема про властивість відповідних кутів при перетині паралельних прямих і січної).
2) Кути 1 і 3 є внутрішніми різносторонніми кутами при перетині паралельних прямих січною, тому рівні (наслідок 1 про властивість відповідних кутів при перетині паралельних прямих і січної).
3) Сума внутрішніх односторонніх кутів 1 і 4 дорівнює 180°, оскільки с – січна до паралельних прямих а і b (наслідок 2 про властивість відповідних кутів при перетині паралельних прямих і січної).
Завдання 213 На малюнку 10.6 прямі a і b паралельні, c – січна.
1) Кути 1 і 8; 6 і 3 є відповідними при перетині паралельних прямих січною, тому рівними (теорема про властивість відповідних кутів при перетині паралельних прямих і січної).
2) Кути 2 і 4 є внутрішніми різносторонніми кутами при перетині паралельних прямих січною, тому рівні (наслідок 1 про властивість відповідних кутів при перетині паралельних прямих і січної).
3) Сума внутрішніх односторонніх кутів 2 і 3 дорівнює 180°, оскільки с – січна до паралельних прямих а і b (наслідок 2 про властивість відповідних кутів при перетині паралельних прямих і січної).
Завдання 214
На малюнку 10.7 прямі m || n, d – січна. Знайдіть ∠1, ∠2, ∠3.
Відповідні кути рівні, тому ∠1 = 110°.
Внутрішні різносторонні кути рівні, тому ∠3 = 110°.
Сума внутрішніх рівносторонніх кутів дорівнює 180°, тому ∠2 = 180° – 110° = 70°.
Завдання 215
На малюнку 10.8 прямі m || n, d – січна. Знайдіть ∠1, ∠2, ∠3.
Відповідні кути рівні, тому ∠1 = 60°.
Кути 1 і 3 – вертикальні, тому ∠3 = ∠1 = 60°.
Кути 1 і 2 суміжні, тому ∠1 + ∠2 = 180°, тоді ∠2 = 180° – ∠1 = 180° – 60° = 120°.
Завдання 216
Градусна міра одного з кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 140°. Знайдіть градусні міри решти семи кутів.
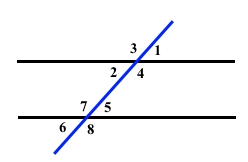
Нехай кут ∠4 = 140°.
Сума внутрішніх односторонніх кутів дорівнює ∠4 + ∠5 = 180°, тоді інший внутрішній односторонній кут дорівнює ∠5 = 180° – ∠4 = 180° – 140° = 40°.
Внутрішні різносторонні кути рівні, тому ∠2 = ∠5 = 40°, ∠7 = ∠4 = 140°.
Розглянемо відповідні кути.
Кути 1 і 5 – відповідні, тому ∠1 = ∠2 = 40°.
Кути 3 і 7 – відповідні, тому ∠3 = ∠7 = 140°.
Кути 8 і 4 – відповідні, тому ∠8 = ∠4 = 140°.
Кути 6 і 2 – відповідні, тому ∠6 = ∠2 = 40°.
Відповідь: утворилося ще три кути по 140°, чотири кути по 40°.
Завдання 217 Один з кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 50°. Знайдіть інші сім кутів.

Нехай кут ∠2 = 50°.
Сума внутрішніх односторонніх кутів дорівнює ∠2 + ∠7 = 180°, тоді інший внутрішній односторонній кут дорівнює ∠7 = 180° – ∠2 = 180° – 50° = 130°.
Внутрішні різносторонні кути рівні, тому ∠5 = ∠2 = 50°, ∠4 = ∠7 = 130°.
Розглянемо відповідні кути.
Кути 1 і 5 – відповідні, тому ∠1 = ∠2 = 50°.
Кути 3 і 7 – відповідні, тому ∠3 = ∠7 = 130°.
Кути 8 і 4 – відповідні, тому ∠8 = ∠4 = 130°.
Кути 6 і 2 – відповідні, тому ∠6 = ∠2 = 50°.
Відповідь: утворилося ще три кути по 50°, чотири кути по 130°.
Завдання 218
1) Один з кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 37°. Чи може один з решти семи кутів дорівнювати 133°?
Якщо прямі паралельні, тоді із січною вони утворюють вісім кутів, по чотири з яких рівних.
Знайдемо суму внутрішніх односторонніх кутів 37° + 133° = 170° ≠ 180°. Оскільки прямі паралельні, тоді один з решти семи кутів не може дорівнювати 133°.
Відповідь: ні.
2) Один з кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 37°. Чи може один з решти семи кутів дорівнювати 143°?
Якщо прямі паралельні, тоді із січною вони утворюють вісім кутів, по чотири з яких рівних.
Знайдемо суму внутрішніх односторонніх кутів 37° + 143° = 180°. Оскільки прямі паралельні, тоді один з решти семи кутів може дорівнювати 143°.
Відповідь: так.
3) Один з кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 37°. Чи може один з решти семи кутів дорівнювати 153°?
Якщо прямі паралельні, тоді із січною вони утворюють вісім кутів, по чотири з яких рівних.
Знайдемо суму внутрішніх односторонніх кутів 37° + 153° = 190° ≠ 180°. Оскільки прямі паралельні, тоді один з решти семи кутів не може дорівнювати 153°.
Відповідь: ні.
Завдання 219 Побудова паралельних прямих
Дано паралельні прямі a і b та точку M, що не належить жодній з прямих. Через точку M паралельно прямій a проведено пряму m. Чи паралельні прямі b і m?
Дано b || а, та m || а. Згідно теореми (властивості паралельних прямих) прямі b і m паралельні третій прямій а, паралельні одна одній. Отже, b || m.
Завдання 220
Знайдіть градусну міру кожного з двох внутрішніх різносторонніх кутів, що утворилися при перетині двох паралельних прямих січною, якщо їх сума дорівнює 240°.
При перетині двох паралельних прямих січною внутрішні різносторонні кути рівні. Якщо їхня сума дорівнює 240°, тоді кожний з них дорівнює 240° : 2 = 120°.
Один із зовнішніх різносторонніх кутів буде в парі внутрішніх односторонніх кутів, тоді знайдемо інший внутрішній односторонній кут 180° – 120° = 60°.
Відповідь: 60° і 120°.
Завдання 221
Сума двох відповідних кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 108°. Знайдіть ці кути.
При перетині двох паралельних прямих січною відповідні кути рівні. Якщо їхня сума дорівнює 108°, тоді кожний з них дорівнює 108° : 2 = 54°.
Відповідь: 54° і 54°.
Завдання 222 Малюнок 10.9.
Дано дві січні c і d до прямих а і b, причому ∠1 = ∠2.
Доведемо, що ∠3 + ∠4 = 180°.
Для прямих а і b та січної с кути 1 і 2 – внутрішні різносторонні кути. Якщо вони рівні, тоді прямі а і b – паралельні.
Для паралельних прямих а і b та січної d кути 3 і 4 – внутрішні односторонні, їхня сума дорівнює 180°. Отже, ∠3 + ∠4 = 180°.
Завдання 223 Малюнок 10.10.
Дано дві січні c і d до прямих а і b, причому ∠1 + ∠2 = 180°.
Доведемо, що ∠3 = ∠4.
Для прямих а і b та січної с кути 1 і 2 – внутрішні односторонні кути. Якщо їхня сума дорівнює 180°, тоді прямі а і b – паралельні.
Для паралельних прямих а і b та січної d кути 3 і 4 – внутрішні різносторонні. Вони є рівними. Отже, ∠3 = ∠4.
Завдання 224 Малюнок 10.11.
Дано дві січні c і d до прямих а і b, причому ∠1 = ∠2, c ﬩ a.
Доведемо, що c ﬩ b.
Для прямих а і b та січної с кути 1 і 2 – відповідні кути. Якщо вони рівні, тоді прямі а і b – паралельні.
Якщо пряма с перпендикулярна до одної з паралельних прямих а, тоді вона перпендикулярна до іншої паралельної прямої b.
Отже, c ﬩ b.
Завдання 225 Малюнок 10.12
Дано дві січні c і d до прямих а і b, причому a ﬩ d, b ﬩ d.
Доведемо, що ∠1 = ∠2.
За ознакою паралельності прямих дві прямі а і b перпендикулярні до третьої прямої d, паралельні.
Для паралельних прямих a і b та січної с кути 1 і 2 – відповідні кути, а вони рівні.
Отже, ∠1 = ∠2.
Завдання 226
1) Знайдіть градусну міру кожного з двох внутрішніх односторонніх кутів, що утворилися при перетині двох паралельних прямих січною, якщо один з них на 16° більший за другий.
При перетині двох паралельних прямих січною сума внутрішніх односторонніх кутів дорівнює 180°.
Нехай х (°) – менший внутрішній односторонній кут, тоді х + 16 (°) – більший внутрішній односторонній кут. Складемо рівняння.
х + х + 16 = 180
2х + 16 = 180
2х = 180 – 16
2х = 164
х = 164 : 2 = (160 + 4) : 2 = 82 (°) – менший внутрішній односторонній кут.
х + 16 = 82 + 16 = 98 (°) – більший внутрішній односторонній кут.
Відповідь: 82° і 98°.
2) Знайдіть градусну міру кожного з двох внутрішніх односторонніх кутів, що утворилися при перетині двох паралельних прямих січною, якщо один з них утричі менший від другого.
При перетині двох паралельних прямих січною сума внутрішніх односторонніх кутів дорівнює 180°.
Нехай х (°) – менший внутрішній односторонній кут, тоді 3х (°) – більший внутрішній односторонній кут. Складемо рівняння.
х + 3х = 180
4х = 180
х = 180 : 4 = (160 + 20) : 4 = 45 (°) – менший внутрішній односторонній кут.
3х = 45 • 3 = (40 + 5) • 3 = 135 (°) – більший внутрішній односторонній кут.
Відповідь: 45° і 135°.
3) Знайдіть градусну міру кожного з двох внутрішніх односторонніх кутів, що утворилися при перетині двох паралельних прямих січною, якщо їхні градусні міри відносяться як 5 : 7.
При перетині двох паралельних прямих січною сума внутрішніх односторонніх кутів дорівнює 180°.
Нехай х (°) – градусна міра одної частини, тоді 5х (°) – менший внутрішній односторонній кут, 7х (°) – більший внутрішній односторонній кут. Складемо рівняння.
5х + 7х = 180
12х = 180
х = 180 : 12 = 180 : 3 : 4 = 15 (°) – градусна міра одної частини.
5х = 15 • 5 = (10 + 5) • 5 = 75 (°) – менший внутрішній односторонній кут.
7х = 15 • 7 = (10 + 5) • 7 = 105 (°) – більший внутрішній односторонній кут.
Відповідь: 75° і 105°.
Завдання 227
1) Знайдіть градусну міру кожного з двох внутрішніх односторонніх кутів, що утворилися при перетині двох паралельних прямих січною, якщо один з них у 4 рази більший за другий.
При перетині двох паралельних прямих січною сума внутрішніх односторонніх кутів дорівнює 180°.
Нехай х (°) – менший внутрішній односторонній кут, тоді 4х (°) – більший внутрішній односторонній кут. Складемо рівняння.
х + 4х = 180
5х = 180
х = 180 : 5 = (150 + 30) : 5 = 36 (°) – менший внутрішній односторонній кут.
4х = 36 • 4 = (30 + 6) • 4 = 144 (°) – більший внутрішній односторонній кут.
Відповідь: 36° і 144°.
2) Знайдіть градусну міру кожного з двох внутрішніх односторонніх кутів, що утворилися при перетині двох паралельних прямих січною, якщо один з них на 8° менший від другого.
При перетині двох паралельних прямих січною сума внутрішніх односторонніх кутів дорівнює 180°.
Нехай х (°) – менший внутрішній односторонній кут, тоді х + 8 (°) – більший внутрішній односторонній кут. Складемо рівняння.
х + х + 8 = 180
2х + 8 = 180
2х = 180 – 8
2х = 172
х = 172 : 2 = (160 + 12) : 2 = 86 (°) – менший внутрішній односторонній кут.
х + 8 = 86 + 8 = 94 (°) – більший внутрішній односторонній кут.
Відповідь: 86° і 94°.
3) Знайдіть градусну міру кожного з двох внутрішніх односторонніх кутів, що утворилися при перетині двох паралельних прямих січною, якщо їхні градусні міри відносяться як 5 : 4.
При перетині двох паралельних прямих січною сума внутрішніх односторонніх кутів дорівнює 180°.
Нехай х (°) – градусна міра одної частини, тоді 4х (°) – менший внутрішній односторонній кут, 5х (°) – більший внутрішній односторонній кут. Складемо рівняння.
4х + 5х = 180
9х = 180
х = 180 : 9 = 20 (°) – градусна міра одної частини.
4х = 20 • 4 = 80 (°) – менший внутрішній односторонній кут.
5х = 20 • 5 = 100 (°) – більший внутрішній односторонній кут.
Відповідь: 80° і 100°.
Завдання 228
1) Знайдіть градусну міру кута x на малюнку 10.13.
При перетині кожної із двох прямих січною зліва бачимо вертикальні кути по 120°. Для цих двох прямих і січної вони утворюють рівні відповідні кути, тому горизонтальні прямі паралельні.
Шуканий кут х є вертикальним кутом до внутрішнього одностороннього кута у парі з кутом 110° при паралельних прямих і січній справа, тому ∠х = 180° – 110° = 70°.
Відповідь: ∠х = 70°.
1) Знайдіть градусну міру кута x на малюнку 10.14.
При перетині кожною із двох прямих нижньою січною бачимо вертикальні кути по 125° і по 55°. Для цих двох прямих і січної сума внутрішніх односторонніх кутів дорівнює 125° + 55° = 180°, тому прямі паралельні.
Шуканий кут х є відповідним до кута 65° для паралельних прямих і верхньої січної, тому вони рівні.
Відповідь: ∠х = 65°.
1) Знайдіть градусну міру кута x на малюнку 10.15.
При перетині кожної із двох прямих січною зліва бачимо, що сума внутрішніх односторонніх кутів дорівнює 125° + 55° = 180°, отже прямі паралельні.
Шуканий кут х є внутрішнім одностороннім до кута 51° при паралельних прямих і січній справа, тому ∠х = 180° – 51° = 129°.
Відповідь: ∠х = 129°.
Завдання 229
1) Знайдіть градусну міру кута x на малюнку 10.16.
При перетині кожної із двох прямих січною зліва бачимо вертикальні кути по 80°. Для цих двох прямих і січної вони утворюють рівні відповідні кути, тому горизонтальні прямі паралельні.
Шуканий кут х є вертикальним кутом до внутрішнього різностороннього кута у парі з кутом 50° при паралельних прямих і січній справа, тому ∠х = 50°.
Відповідь: ∠х = 50°.
1) Знайдіть градусну міру кута x на малюнку 10.17.
При перетині кожною із двох прямих нижньою січною бачимо вертикальні кути по 130° і по 50°. Для цих двох прямих і нижньої січної сума внутрішніх односторонніх кутів дорівнює 130° + 50° = 180°, тому прямі паралельні.
Шуканий кут х є внутрішнім одностороннім кутом у парі з кутом 70° для паралельних прямих і верхньої січної, тому ∠х = 180° – 70° = 110°.
Відповідь: ∠х = 110°.
Завдання 230
Прямі a і b не паралельні прямій m. Чи можна зробити висновок, що прямі a і b не паралельні між собою?
Якщо a і b не паралельні прямій m, тоді вони перетинаються з прямою m – вона є січною. Самі ж прямі a і b можуть або перетинатися, або бути паралельними між собою.
Відповідь: ні.
Завдання 231
Сума градусних мір трьох з восьми кутів, що утворилися при перетині паралельних прямих січною, дорівнює 120°. Знайдіть градусні міри кожного з восьми кутів.
При перетині паралельних прямих із січною утворюється вісім кутів, з них по чотири однакових гострі та тупі кути. Усі прямі кути не підходять, бо сума трьох прямих кутів завжди більша за 120°.
Відомо, що градусна міра трьох кутів дорівнює 120°. Сума гострого і тупого внутрішніх односторонніх кутів дорівнює 180°. Тому не підходять 3 тупі кути, 2 тупі і 1 гострий, 1 тупий і 2 гострий.
Можемо мати суму трьох однакових гострих кутів, тоді 120° : 3° = 40° – гострі кути.
Для паралельних прямих і січної сума внутрішніх односторонніх кутів дорівнює 180°, тому 180° – 40° = 140° – тупі кути.
Відповідь: 40°, 40°, 40°, 40°, 140°, 140°, 140°, 140°.
Завдання 232
Сума градусних мір чотирьох з восьми кутів, що утворилися при перетині паралельних прямих січною, дорівнює 128°. Знайдіть градусні міри кожного з восьми кутів.
При перетині паралельних прямих із січною утворюється вісім кутів, з них по чотири однакових гострі та тупі кути. Усі прямі кути не підходять, бо сума чотирьох прямих кутів завжди більша за 128°.
Відомо, що градусна міра чотирьох кутів дорівнює 128°. Сума гострого і тупого внутрішніх односторонніх кутів дорівнює 180°. Тому не підходять 4 тупі кути, 3 тупі і 1 гострий, 2 тупі і 2 гострі, 1 тупий і 3 гострих.
Можемо мати суму чотирьох однакових гострих кутів, тоді 128° : 4° = 32° – гострі кути.
Для паралельних прямих і січної сума внутрішніх односторонніх кутів дорівнює 180°, тому 180° – 32° = 148° – тупі кути.
Відповідь: 32°, 32°, 32°, 32°, 148°, 148°, 148°, 148°.
Завдання 233
Дано AB || CD. Знайдіть ∠CMA.
Через точку М проведемо пряму OP, паралельну АВ, якщо пряма OP || AB і CD || AB, тоді за властивістю паралельних прямих ОР || CD.
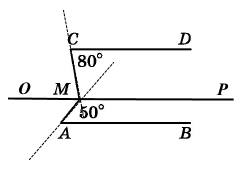
Для променя МО, що проходить між сторонами кута АМС справедлива властивість вимірювання кутів: ∠АМС = ∠АМО + ∠ОМС.
Для ОР || CD і січної МС маємо рівні внутрішні різносторонні кути ∠ОМС = ∠MCD = 80°.
Для ОР || АВ і січної AМ маємо рівні внутрішні різносторонні кути ∠AMO = ∠MAB = 50°.
∠АМС = ∠АМО + ∠ОМС = 80° + 50° = 130°.
Відповідь: ∠АМС = 130°.
Завдання 234
Дано MN || PL. Знайдіть ∠MKP.
Через точку К проведемо пряму АВ, паралельну до PL, якщо пряма AB || PL і MN || PL, тоді за властивістю паралельних прямих АВ || MN.
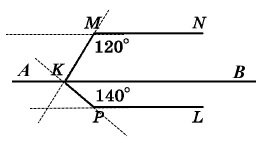
Для променя KB, що проходить між сторонами кута MKP справедлива властивість вимірювання кутів: ∠MKP = ∠MKB + ∠BKP.
Для AB || PL і січної KP внутрішній односторонній кут ∠ВКР = 180° – 140° = 40°.
Для АВ || NM і січної KМ внутрішній односторонній кут ∠МКВ = 180° – 120° = 60°.
∠MKP = ∠MKB + ∠BKP = 60° + 40° = 100°.
Відповідь: ∠МKP = 100°.
Завдання 235 Доведіть, що бісектриси пари внутрішніх різносторонніх кутів, утворених при перетині двох паралельних прямих січною, паралельні.
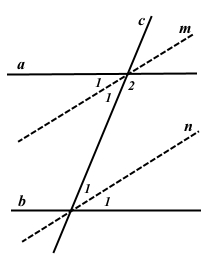
Бісектриси пари внутрішніх різносторонніх кутів поділять їх пополам.
При перетині двох паралельних прямих a і b та січною с внутрішні різносторонні кути рівні, а сума внутрішніх односторонніх кутів дорівнює 180°. Поділені бісектрисою всі кути рівні між собою, також рівні до них вертикальні кути, а сума внутрішніх односторонніх кутів дорівнює ∠2 + (∠1 + ∠1) = 180°.
Для прямих m і n, на яких лежать бісектриси внутрішніх різносторонніх кутів, та січної с знайдемо суму внутрішніх кутів ∠1 + ∠2 + ∠1 = ∠2 + (∠1 + ∠1) = 180°, тому прямі m і n паралельні. Оскільки бісектриси лежать на паралельних прямих, то за означенням вони паралельні.
Завдання 236 Доведіть, що бісектриси пари відповідних кутів, утворених при перетині двох паралельних прямих січною, паралельні.
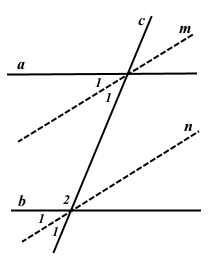
Бісектриси пари відповідних кутів поділять їх пополам.
При перетині двох паралельних прямих a і b та січною с відповідні кути рівні, а сума внутрішніх односторонніх кутів дорівнює 180°. Поділені бісектрисою всі кути рівні між собою, також рівні до них вертикальні кути, а сума внутрішніх односторонніх кутів дорівнює ∠2 + (∠1 + ∠1) = 180°.
Для прямих m і n, на яких лежать бісектриси внутрішніх різносторонніх кутів, та січної с знайдемо суму внутрішніх кутів ∠1 + ∠2 + ∠1 = ∠2 + (∠1 + ∠1) = 180°, тому прямі m і n паралельні. Оскільки бісектриси лежать на паралельних прямих, то за означенням вони паралельні.
Вправи для повторення
Завдання 237
Накресліть відрізок AB, промінь CD та пряму a так, щоб відрізок AB був перпендикулярним до променя CD, але не перетинав його, а промінь CD був паралельний прямій a.
Відрізок АВ і промінь CD мають лежати на перпендикулярних прямих, причому пряма, на якій лежить промінь CD, має бути паралельна прямій а.
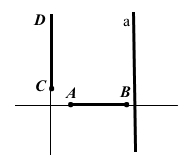
Завдання 238
1) Точка C належить відрізку AB завдовжки 16 см. Знайдіть відрізки AC і BC, якщо AC більший за BC на 2 см.
Якщо точка С належить відрізку АВ, тоді за властивістю вимірювання відрізків АВ = АС + ВС.
Нехай х (см) – відрізок ВС, тоді х + 2 (см) – відрізок АС. Складемо рівняння.
х + х + 2 = 16
2х + 2 = 16
2х = 16 – 2
2х = 14
х = 14 : 2
х = 7 (см) – довжина відрізка ВС.
х + 2 = 7 + 2 = 9 (см) – довжина відрізка АС.
Відповідь: АС = 9 см (Н), ВС = 7 см (А).
2) Точка C належить відрізку AB завдовжки 16 см. Знайдіть відрізки AC і BC, якщо AC більший за BC утричі.
Якщо точка С належить відрізку АВ, тоді за властивістю вимірювання відрізків АВ = АС + ВС.
Нехай х (см) – відрізок ВС, тоді 3х (см) – відрізок АС. Складемо рівняння.
х + 3х = 16
4х = 16
х = 16 : 4
х = 4 (см) – довжина відрізка ВС.
3х = 4 • 3 = 12 (см) – довжина відрізка АС.
Відповідь: АС = 12 см (О), ВС = 4 см (Ф).
3) Точка C належить відрізку AB завдовжки 16 см. Знайдіть відрізки AC і BC, якщо AC : BC = 5 : 3.
Якщо точка С належить відрізку АВ, тоді за властивістю вимірювання відрізків АВ = АС + ВС.
Нехай х (см) – градусна міра 1 частини, тоді 3х (см) – відрізок ВС, 5х (см) – відрізок АС. Складемо рівняння.
3х + 5х = 16
8х = 16
х = 16 : 2
х = 2 (см) – довжина 1 частини.
3х = 2 • 3 = 6 (см) – довжина відрізка ВС.
5х = 2 • 5 = 10 (см) – довжина відрізка АС.
Відповідь: АС = 10 см (К), ВС = 6 см (Р).
Іван Франко — письменник, учений, перекладач, громадський діяч...
Прізвище видатного українського письменника:
|
4 см |
6 см |
7 см |
9 см |
10 см |
12 см |
|
Ф |
Р |
А |
Н |
К |
О |
Життєва математика
Завдання 239 Щоб засіяти 1 м2 землі, потрібно 40 г насіння газонної трави. Кілограм такого насіння коштує 90 грн. Скільки коштів потрібно, щоб засіяти газонною травою клумбу у формі квадрата, сторона якого 20 м?
Розв’язання
Короткий запис
Сторона — 20 м
S — ?
1) 20 • 20 = 400 (м2) – площа квадратної клумби.
Короткий запис
1 м2 — 40 г
400 м2 — ? г
2) 40 • 400 = 16000 (г) = 16 (кг) – маса насіння.
Короткий запис
1 кг — 90 грн
16 кг — ? грн
3) 90 • 16 = 90 • (10 + 6) = 900 + 540 = 1440 (грн) – потрібно коштів (вартість насіння).
Відповідь: потрібно 1440 гривень.
Підготуйтеся до вивчення нового матеріалу
Завдання 240 Накресліть трикутник АВС, у якого АВ = 3 см, АС = 4 см. Виміряйте сторону ВС цього трикутника та знайдіть його периметр.
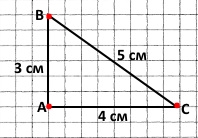
Р = АВ + АС + ВС = 3 см + 4 см + 5 см = 12 см.
Завдання 241 Одна сторона трикутника дорівнює 8 см, друга – 7 см. Знайдіть довжину третьої сторони трикутника, якщо його периметр дорівнює 20 см.
Короткий запис
І сторона — 8 см
ІІ сторона — 7 см
ІІІ сторона — ? см
Периметр (всього) — 20 см
Розв’язання
1) 8 + 7 = 15 (см) – сума довжин двох сторін.
3) 20 – 15 = 5 (см) – довжина третьої сторони трикутника.
Відповідь: довжина третьої сторони трикутника 5 сантиметрів.
Завдання 242 Не відриваючи олівця від паперу, проведіть через дев'ять точок чотири відрізки.