Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
ВПРАВИ ДЛЯ ПОВТОРЕННЯ РОЗДІЛУ 2
До § 5
Завдання 243
За означенням суміжні кути – це два кути, одна сторона яких є спільною, а дві інші сторони цих кутів є доповняльними променями, тобто утворюють розгорнутий кут. Сума суміжних кутів дорівнює 180°.
На малюнку 1 суміжні кути 3 і 2.
На малюнку 2 суміжні кути 1 і 4, 2 і 3.
На малюнку 3 суміжні кути 1 і 2, 3 і 4.
Завдання 244
1) Чи можна, використовуючи лише олівець та лінійку, побудувати кут, суміжний з даним?
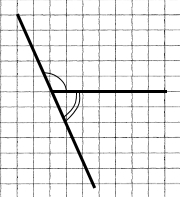
Можна. Треба продовжити сторону так, щоб від вершини кута відкласти доповняльний промінь у протилежну сторону.
2) Скільки таких кутів можна побудувати?
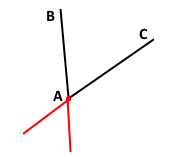
Можна побудувати дві пари суміжних кутів.
Завдання 245
∠ABC менший, ніж ∠MNP. У якого з кутів суміжний кут більший?
Оскільки сума суміжних кутів стала (дорівнює 180°), у меншого кута АВС буде більший суміжний кут.
Відповідь: у ∠ABC.
Завдання 246
Знайдіть суміжні кути, якщо їхні градусні міри відносяться як 3 : 7.
Сума суміжних кутів дорівнює 180°.
Нехай х (°) – градусна міра одної частини, тоді 3х (°) – менший суміжний кут, 7х (°) – більший суміжний кут. Складемо рівняння.
3х + 7х = 180
10х = 180
х = 180 : 10
х = 18 (°) – градусна міра одної частини.
3х = 18 • 3 = 54 (°) – менший суміжний кут.
7х = 18 • 7 = 126 (°) – більший суміжний кут.
Відповідь: 54° і 126°.
До § 5
Завдання 247
Один із суміжних кутів становить 20% від іншого. Знайдіть ці кути.
Сума суміжних кутів дорівнює 180°.
Нехай х (°) – більший суміжний кут, тоді 0,2х (°) – менший суміжний кут. Складемо рівняння.
х + 0,2х = 180
1,2х = 180
х = 180 : 1,2
х = 150 (°) – більший суміжний кут.
0,2х = 150 • 0,2 = 30 (°) – менший суміжний кут.
Відповідь: 30° і 150°.
Завдання 248
Один із суміжних кутів на 20% менший від іншого. Знайдіть ці кути.
Сума суміжних кутів дорівнює 180°.
Нехай х (°) – більший суміжний кут, тоді х – 0,2х (°) – менший суміжний кут. Складемо рівняння.
х + (х – 0,2х) = 180
1,8х = 180
х = 180 : 1,8
х = 100 (°) – більший суміжний кут.
х – 0,2х = 0,8х = 100 • 0,8 = 80 (°) – менший суміжний кут.
Відповідь: 80° і 100°.
Завдання 249
Бісектриса кута ABC утворює зі стороною кут, удвічі більший за кут, суміжний з кутом ABC. Знайдіть ∠ABC.
Бісектриса кута ABC ділить його пополам. Якщо вона утворює зі стороною кут, удвічі більший за кут, суміжний з кутом ABC, тоді можна стверджувати, що кут АВС у 4 рази більший за суміжний.
Сума суміжних кутів дорівнює 180°.
Нехай х (°) – суміжний кут, тоді 4х (°) – кут АВС. Складемо рівняння.
х + 4х = 180
5х = 180
х = 180 : 5
х = (150 + 30) : 5
х = 36 (°) – суміжний кут.
4х = 36 • 4 = 144 (°) – кут АВС.
Відповідь: 54° і 126°.
До § 6
Завдання 250
Предмет домашнього вжитку дає уявлення про вертикальні кути: ножиці.
Завдання 251
Вертикальні кути утворюються при перетині двох прямих.
На малюнку 5, 6, 8 кути 1 і 2 є вертикальними.
Завдання 252 Правильне твердження.
1) якщо два кути рівні, то вони вертикальні (хибне);
2) якщо два кути зі спільною вершиною рівні, то вони вертикальні (хибне);
3) для кожного кута, меншого від розгорнутого, можна добудувати тільки один вертикальний кут (хибне);
4) для кожного кута, меншого від розгорнутого, можна добудувати тільки один суміжний кут (істинне).
Завдання 253 При перетині двох прямих утворилося чотири кути.
При перетині двох прямих утворюється дві пари вертикальних кутів. Вертикальні кути рівні.
При перетині двох прямих також утворюються дві пари суміжних кутів. Сума суміжних кутів дорівнює 180°.
1) Чи можуть деякі два з них дорівнювати 5° і 175°?
Нерівні кути мають бути суміжними.
5° + 175° = 180 – маємо суміжні кути.
Відповідь: так.
2) Чи можуть деякі два з них дорівнювати 15° і 19°?
Нерівні кути мають бути суміжними.
15° + 19° < 180°, не може бути таких кутів.
Відповідь: ні.
3) При перетині двох прямих утворилося чотири кути. Чи можуть деякі два з них дорівнювати 27° і 154°?
Нерівні кути мають бути суміжними.
27° + 154° = 181° > 180°, не може бути таких кутів.
Відповідь: ні.
4) При перетині двох прямих утворилося чотири кути. Чи можуть деякі два з них дорівнювати 3° і 3°?
Два рівні кути можуть бути вертикальними.
Відповідь: так.
Завдання 254
Один з кутів, що утворилися при перетині двох прямих, на 48° більший за інший. Знайдіть кут між прямими.
При перетині двох прямих утворюються пари суміжних кутів. Сума суміжних кутів дорівнює 180°. Кут між прямими не перевищує 90°.
Нехай х (°) – менший кут, тоді х + 48 (°) – більший суміжний кут. Складемо рівняння.
х + (х + 48) = 180
2х + 48 = 180
2х = 180 – 48
2х = 132
х = 132 : 2
х = (120 + 12) : 2
х = 66 (°) – менший кут, він і буде шуканим кутом між прямими.
Відповідь: 66°.
Завдання 255 Один з кутів, що утворилися при перетині двох прямих, дорівнює сумі двох суміжних з ним. Знайдіть цей кут.
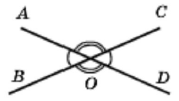
При перетині двох прямих утворюється дві пари суміжних. Якщо кут дорівнює сумі двох суміжних з ним, тоді кут удвічі менший за суміжний.
Нехай х (°) – менший кут, 2х (°) – більший суміжний кут. Складемо рівняння.
х + 2х = 180
3х = 180
х = 180 : 3 = 60 (°) – менший кут.
Відповідь: 60°.
Завдання 256
1) Знайдіть градусну міру кожного із чотирьох кутів, що утворилися при перетині двох прямих, якщо сума двох із цих кутів менша від суми двох інших у 4 рази.
Сума суміжних кутів дорівнює 180°. Якщо сума двох із кутів менша від суми двох інших у 4 рази, то йдеться про вертикальні кути. Вертикальні кути різних пар є суміжними, тому сума всіх утворених вертикальних кутів дорівнює 360°. Вертикальні кути рівні.
Нехай х (°) – сума одних вертикальних кутів, тоді 4х (°) – сума інших вертикальних кутів. Складемо рівняння.
х + 4х = 360
5х = 360
х = 360 : 5
х = (350 + 10) : 5
х = 72 (°) – сума одних вертикальних кутів.
4х = 72 • 4 = 288 (°) – сума інших вертикальних кутів.
72 : 2 = (60 + 12) : 2 = 36 (°) – одні вертикальні кути.
288 : 2 = (200 + 80 + 8) : 2 = 144 (°) – інші вертикальні кути.
Відповідь: 36°, 36°, 144°, 144°.
2) Знайдіть градусну міру кожного із чотирьох кутів, що утворилися при перетині двох прямих, якщо сума двох із цих кутів більша за суму двох інших на 160°.
Сума суміжних кутів дорівнює 180°. Якщо сума двох із кутів менша від суми двох інших, то йдеться про вертикальні кути. Вертикальні кути різних пар є суміжними, тому сума всіх утворених вертикальних кутів дорівнює 360°. Вертикальні кути рівні.
Нехай х (°) – сума одних вертикальних кутів, тоді х + 160 (°) – сума інших вертикальних кутів. Складемо рівняння.
х + (х + 160) = 360
2х + 160 = 360
2х = 360 – 160
2х = 200
х = 200 : 2
х = 100 (°) – сума одних вертикальних кутів.
х + 160 = 100 + 160 = 260 (°) – сума інших вертикальних кутів.
100 : 2 = 50 (°) – одні вертикальні кути.
260 : 2 = (200 + 60) : 2 = 130 (°) – інші вертикальні кути.
Відповідь: 50°, 50°, 230°, 230°.
Завдання 257
Знайдіть кут між прямими, які перетинаються, якщо один з кутів, що утворилися, у 8 разів менший від суми трьох інших кутів.
Між прямими, що перетинаються утворюються дві пари суміжних кутів. Сума суміжних кутів дорівнює 180°, тому сума всіх кутів дорівнює 360°. Кут між прямими не перевищує 90°.
Нехай х (°) – один кут, тоді 8х (°) – сума трьох інших кутів. Складемо рівняння.
х + 8х = 360
9х = 360
х = 360 : 9
х = 40 (°) – один кут, він буде шуканим кутом між прямими.
Відповідь: 40°.
До § 7
Завдання 258 Побудова перпендикулярних прямих
Накресліть пряму а та позначте точку M, що їй не належить. За допомогою косинця проведіть з точки M перпендикуляр до прямої а. Виміряйте відстань від точки M до прямої а.
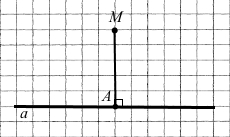
МА = 25 мм = 2 см 5 мм
Завдання 259
Накресліть гострий ∠KAM, позначте на стороні AK точку B. Побудуйте за допомогою косинця пряму, що проходить через точку B перпендикулярно до AK.
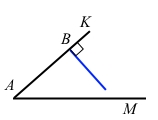
Завдання 260
Накресліть промінь AB і відрізок KP так, щоб вони були перпендикулярними і не перетиналися.
Промінь AB і відрізок KP перпендикулярні (AB ⊥ KP), якщо вони лежать на перпендикулярних прямих.
Для простоти побудови спочатку можна намалювати перпендикулярні прямі, а потім нанести потрібні фігури так, щоб вони не перетиналися.
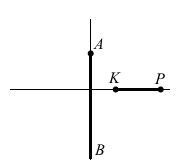
Завдання 261 Малюнок 9.
Усі пари перпендикулярних між собою відрізків: CD ⊥ AB, DK ⊥ AB, CK ⊥ AB.
Завдання 262 Малюнок 10.
1) Прямі AB ⊥ CD, ∠KOC = ∠COL. Чи правильно, що ∠AOK = ∠LOB, ∠AOL = ∠KOB?
Якщо AB ⊥ CD, тоді вони перетинаються під прямим кутом, усі кути прямі, наприклад, ∠АОС = ∠СОВ = 90°.
Для променя ОК між сторонами кута АОС за основною властивістю вимірювання кутів ∠АОС = 90° = ∠АОК + ∠КОС.
Для променя ОL між сторонами кута CОB за основною властивістю вимірювання кутів ∠CОB = 90° = ∠COL + ∠LOB = ∠КОС + ∠LOB.
90° = ∠LOB + ∠KOC.
Якщо рівні ліві частини нерівності, тоді рівні праві частини, тому ∠AOK = ∠LOB.
Тепер розглянемо кути AOL і KOB.
Для променя ОС між сторонами кута АОL за основною властивістю вимірювання кутів ∠АОL = ∠АОC + ∠COL, ∠АОL = 90° + ∠КОС, ∠АОL = ∠КОС + 90°.
Для променя ОC між сторонами кута KОB за основною властивістю вимірювання кутів ∠KОB = ∠KOC + ∠COB, ∠KОB = ∠КОС + 90°.
Якщо рівні праві частини нерівності, тоді рівні ліві частини, тому ∠AOL = ∠KOB.
Відповідь: так.
2) Прямі AB ⊥ CD, ∠KOC = ∠COL. Порівняйте ∠KOB і ∠AOK.
Якщо AB ⊥ CD, тоді вони перетинаються під прямим кутом, усі кути прямі, наприклад, ∠АОС = ∠СОВ = 90°.
Для променя ОК між сторонами кута АОС за основною властивістю вимірювання кутів ∠АОС = 90° = ∠АОК + ∠КОС, 90° = ∠АОК + ∠КОС.
Для променя ОL між сторонами кута CОB за основною властивістю вимірювання кутів ∠CОB = 90° = ∠COL + ∠LOB = ∠КОС + ∠LOB.
90° = ∠LOB + ∠KOC.
Якщо рівні ліві частини нерівності, тоді рівні праві частини, тому ∠AOK = ∠LOB.
Для променя ОL між сторонами кута KOB за основною властивістю вимірювання кутів ∠KOB = ∠KOL + ∠LОB = 2∠KOC + ∠AOK.
∠KOB = 2∠KOC + ∠AOK.
У більшого кута більша його градусна міра.
∠KOB > ∠AOK.
Відповідь: ∠KOB > ∠AOK.
Завдання 263
1) Чи можуть два гострих кути бути між собою рівними, якщо в них одна сторона спільна, а дві інші – перпендикулярні між собою?
Для простоти побудови спочатку слід намалювати перпендикулярні прямі, потім нанести перпендикулярні сторони кутів, тоді очевидним стане розміщення спільної сторони.
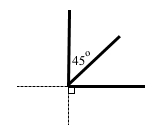
Два гострих кути можуть бути рівними, якщо у них спільна сторона, а дві інші сторони утворених кутів лежать по різні сторони від неї. Якщо ці кути разом утворюють прямий кут, тоді кожен з них може дорівнювати 45°.
Відповідь: так.
2) Чи можуть два тупих кути бути між собою рівними, якщо в них одна сторона спільна, а дві інші – перпендикулярні між собою?
Для простоти побудови спочатку слід намалювати перпендикулярні прямі, потім нанести перпендикулярні сторони кутів, тоді очевидним стане розміщення спільної сторони.
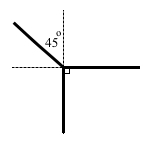
Два тупих кути можуть бути рівними, якщо спільна сторона є бісектрисою вертикального кута до кута, утворених двома іншими сторонами. Тоді кожен з них може дорівнювати 45° + 90° = 135°.
Відповідь: так.
Завдання 264
Використовуючи шаблон кута, градусна міра якого 6°, побудувати взаємно перпендикулярні прямі.
90° = 6° • 15. Тому можна провести горизонтальну пряму. Від неї 15 разів відкласти кут 6°. Вертикальна сторона останнього кута буде перпендикулярною до початкової прямої.
Завдання 265
Доведіть, що коли бісектриси кутів ABC і CBD взаємно перпендикулярні, то точки A, B і D лежать на одній прямій.
Дано ВО – бісектриса кута АВС, ВР – бісектриса кута СВD. ВО ⊥ ВР. Довести, що кут АВD – розгорнутий.
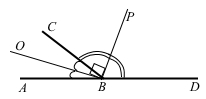
Якщо ВО ⊥ ВР, тоді ∠ОВР = 90°.
Для променя BC між сторонами кута OBP виконується основна властивість вимірювання кутів ∠OBP = 90° = ∠OBC + ∠CBP.
Промінь ВО – бісектриса кута АВС, тоді ∠АВС = 2∠ОВС.
Промінь ВР – бісектриса кута CBD, тоді ∠CBD = 2∠CBP.
Для променя BC між сторонами кута АВD виконується основна властивість вимірювання кутів ∠ABD = ∠ABC + ∠CBD = 2∠OBC + 2∠CBP = 2 (∠OCB + ∠CBP) = 2∠OBP = 2 • 90° = 180°.
Кут ABD є розгорнутим, значить його сторони ВА і BD – є доповняльними променями. Отже, точки А, В і D лежать на одній прямій.
До § 8
Завдання 266 Побудова паралельних прямих
Накресліть відрізки AB і CD так, щоб вони були паралельними між собою.
Паралельні відрізки лежать на паралельних прямих.
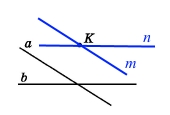
Завдання 267 Малюнок 11.
Дві прямі a і b, що перетинаються, та точка K, що не належить жодній з них. Проведіть через точку K прямі, паралельні прямим a і b.
Через точку, що не належить прямій, можна провести тільки одну пряму паралельну даній. Отже, до кожної з двох прямих зможемо побудувати тільки одну паралельну: m || a, n ||b.
Завдання 268
1) Прямі a і b не перетинаються. Чи можна стверджувати, що прямі паралельні?
Означення паралельних прямих: дві прямі на площині називають паралельними, якщо вони не перетинаються.
Відповідь: так (згідно означення паралельних прямих).
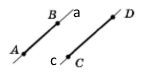
2) Відрізки AB і CD не перетинаються. Чи можна стверджувати, що вони паралельні?
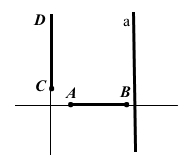
Наприклад відрізки AB і CD не перетинаються, але вони перпендикулярні, бо лежать на перпендикулярних прямих.
Відповідь: ні.
3) Промені MN і KL не перетинаються. Чи можна стверджувати, що вони паралельні?
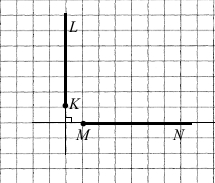
Наприклад промені MN і KL не перетинаються, але вони перпендикулярні, бо лежать на перпендикулярних прямих.
Відповідь: ні.
Завдання 269
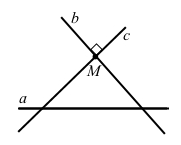
Дано пряму a і точку K, що їй не належить. Через точку K провели дві прямі b і c. Як можуть розміщуватися ці прямі відносно прямої a? Розгляньте всі випадки та виконайте до них малюнки.
Через точку, що не належить прямій, можна провести тільки одну пряму, паралельну даній.
Через точку, що не належить прямій, можна провести тільки одну пряму, перпендикулярну даній.
1) b || a, пряма с – січна, бо перетинає як пряму а, так і пряму b.
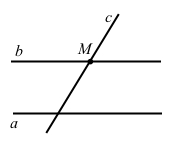
Частковий випадок, коли b || a, с ⊥ а.
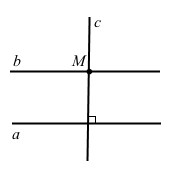
2) с || a, пряма b – січна, бо перетинає як пряму а, так і пряму c.
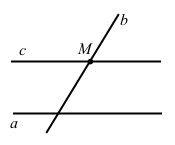
Частковий випадок, коли c || a, b ⊥ а.
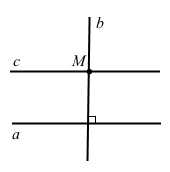
3) прямі b і c перетинаються в точці М та перетинають пряму а.
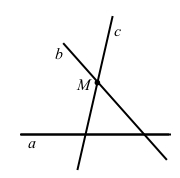
Частковий випадок, коли b ⊥ а.
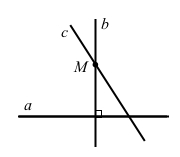
Частковий випадок, коли c ⊥ а.
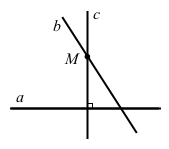
Частковий випадок, коли b ⊥ c.
Завдання 270
Прямі a і b – паралельні, а прямі b і n – перетинаються. Пряма c паралельна прямій b. Доведіть, що пряма c перетинає пряму n і паралельна прямій a.
Дано а || b, с || b, прямі b і n – перетинаються. Довести, що с || а, с і n – перетинаються.
За умовою a || b і c || b. За властивістю паралельних прямих дві прямі а і с, паралельні третій прямій b, паралельні одна одній, отже, с || а.
За умовою прямі с || b, а прямі b і n – перетинаються. Якщо пряма n перетинає одну з двох паралельних прямих b, то вона перетинає і другу c, прямі n і с перетинаються, отже пряма с перетинає пряму n.
До § 9
Завдання 271
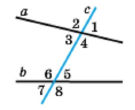
Накреслили дві прямі та їхню січну, пронумерували утворені кути.
Внутрішні односторонні кути: 5 і 4, 3 і 6.
Внутрішні різносторонні кути: 3 і 5, 4 і 6.
Відповідні кути: 2 і 6, 1 і 5, 3 і 7, 4 і 8.
Завдання 272
1) На малюнку 12 прямі m і n не є паралельними, оскільки відповідні кути 71° і 72° нерівні.
2) На малюнку 13 прямі m і n є паралельними, оскільки сума внутрішніх односторонніх кутів 60° + 120° = 180°.
3) На малюнку 14 прямі m і n є паралельними, оскільки внутрішні різносторонні кути 130° і 130° рівні.
4) На малюнку 15 прямі m і n є паралельними, оскільки внутрішні різносторонні кути рівні, один різносторонній кут 45°, а другий є вертикальним до іншого кута 45°.
Завдання 273
При перетині прямих a і b січною c утворилися два між собою рівні гострі кути. Чи можна стверджувати, що a || b?
При перетині прямих a і b січною c, щоб стверджувати, що a || b, кути додатково повинні містити інформацію, яка би задовольняла ознаки або властивості паралельних прямих. Треба уточнення, про які саме кути йдеться.
Наприклад, на малюнку утворилися два однакові між собою рівні кути, проте нема паралельних прямих.
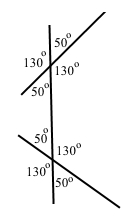
Відповідь: ні.
Завдання 274 Малюнок 16.
Кути ∠1 = ∠2, ∠2 + ∠3 = 180°. Чи є прямі a і c паралельними між собою?
Розглянемо прямі а і b та січну m. Кути 1 і 2 – відповідні, за умовою ∠1 = ∠2, тому прямі b || a.
Розглянемо прямі b і c та січну m. Кут ∠2 – вертикальний до внутрішнього одностороннього кута у парі з кутом ∠3. За умовою ∠2 + ∠3 = 180°, тому прямі b || с.
Маємо дві прямі a і с, паралельні третій прямі b, паралельні одна одній.
Якщо a || b і c || b, тоді прямі a || с.
Відповідь: так.
До § 10
Завдання 275 Малюнок 17.
Прямі m і n – паралельні, c – січна. Знайдіть градусні міри кутів 1, 2, 3, 4.
Кут 130° і кут 2 – внутрішні односторонні кути, тому ∠2 = 180° – 130° = 50°.
Кути 2 і 1 внутрішні різносторонні, вони рівні, тому ∠1 = ∠2 = 50°.
Кути 130° і 3 – внутрішні різносторонні, вони рівні, тому ∠3 = 130°.
Кути 3 і 4 – вертикальні, вони рівні, тому ∠4 = ∠3 = 130°.
Відповідь: ∠1 = 50°, ∠2 = 50°, ∠3 = 130°, ∠4 = 130°.
Завдання 276
Дано: a || b, b || c, c || d. Доведіть, що a || d.
Дві прямі, паралельні третій прямі, паралельні одна одній.
За умовою а || b та с || d, тоді за властивістю паралельних прямих а || с.
Оскільки а || с та d || с, отже, за властивістю паралельних прямих a || d.
Завдання 277
Знайдіть градусну міру кожного з двох внутрішніх односторонніх кутів, що утворилися при перетині двох паралельних прямих січною, якщо один з них становить 80% від другого.
При перетині двох паралельних прямих січною сума внутрішніх односторонніх кутів дорівнює 180°.
Нехай х (°) – один кут (більший, тупий), тоді 0,8х (°) – другий кут (менший, гострий). Складемо рівняння.
х + 0,8х = 180
1,8х = 180
х = 180 : 1,8
х = 100 (°) – один кут.
0,8х = 100 • 0,8 = 80 (°) – другий кут.
Відповідь: 80° і 100°.
Завдання 278 Малюнок 18.
a || b, c || d, ∠1 = 100°. Знайдіть градусні міри кутів 2, 3, 4.
Розглянемо прямі a || b та січну d. Кути 1 і 2 відповідні, вони рівні, тому ∠2 = ∠1 = 100°.
Для прямих а і d, що перетинаються кути 3 і 1 суміжні, тому ∠3 = 180° – ∠1 = 180° – 100° = 80°.
Розглянемо прямі с || d та січну а. Кути 3 і 4 внутрішні різносторонні, вони рівні, тому ∠4 = ∠3 = 80°.
Відповідь: ∠2 = 100°, ∠3 = 80°, ∠4 = 80°.
Завдання 279
Один з внутрішніх односторонніх кутів, що утворилися при перетині паралельних прямих січною, дорівнює 72°. Знайдіть кут між бісектрисами внутрішніх односторонніх кутів.
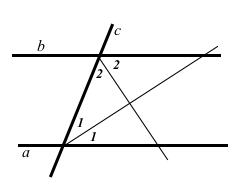
При перетині паралельних прямих січною сума внутрішніх односторонніх кутів дорівнює 180°. Знайдемо інший внутрішній односторонній кут 180° – 72° = 108°.
Бісектриси кутів ділять їх пополам, отримаємо кути 72° = 2∠2, 108° = 2∠1,
звідси ∠2 = 72° : 2 = 36° і ∠1 = 108° : 2 = 54°.
Січна і бісектриси утворюють трикутник, сума кутів трикутника дорівнює 180°. Знайдемо третій кут трикутника, який буде шуканим кутом між бісектрисами внутрішніх односторонніх кутів 180° – (36° + 54°) = 90°.
Відповідь: прямий кут.
Завдання 280 Малюнок 19.
Прямі AB і CD паралельні. Знайдіть ∠MNB.
Через точку N проведемо пряму PN паралельну прямій АВ. Якщо пряма PN || AB і CD || AB, тоді за властивістю паралельних прямих PN || CD.
Через точку M проведемо пряму OM паралельну прямій CD. Якщо пряма OM || CD і PN || CD, тоді за властивістю паралельних прямих OM || PN.
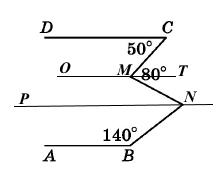
Промінь PN проходить між сторонами кута MNB, тоді за основною властивістю вимірювання кутів ∠MNB = ∠MNP + ∠PNB.
Для паралельних прямих СD і ОМ та січної СМ внутрішні різносторонні кути рівні ∠DCM = ∠CMT = 50°.
Якщо промінь МТ проходить між сторонами кута СМN, тоді за основною властивістю вимірювання кутів ∠СМN = ∠СМТ + ∠ТМN, звідси ∠ТМN = ∠СМN – ∠СМТ = 80° – 50° = 30°.
Для ОМ || PN і січної МN маємо рівні внутрішні різносторонні кути ∠MNP = ∠TMN = 30°.
Для PN || АВ і січної BN сума внутрішніх односторонніх кутів ∠ABN + ∠PNB = 180°, тому
∠PNB = 180° – ∠ABN = 180° – 140° = 40°.
Отже, ∠MNB = ∠MNP + ∠PNB = 30° + 40° = 70°.
Відповідь: ∠MNB = 70°.
Розв'язати геометричні задачі Київських міських олімпіад з математики, що пропонувалися пів століття тому.
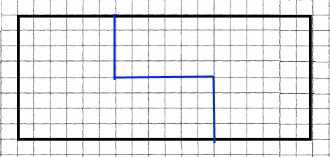
Завдання 1 (1950 р.) Розділіть прямокутник розміром 18 х 8 на дві частини так, щоб з них можна було утворити квадрат.
Для простоти візьмемо прямокутник 18 х 8 клітинок.
Sпр = 18 • 8 = 144 (см)
Таку площу має квадрат зі стороною 12 см (122 = 144).
Завдання 2 (1975 р.) У країні 1000 доріг з'єднують 200 міст, причому з кожного міста виходить хоча б одна дорога. Яку найбільшу кількість доріг можна одночасно закрити на ремонт, не порушуючи при цьому зв'язок між містами?
Якщо із дороги з кожного міста виходить хоча б одна дорога, тоді 200 міст можна об’єднати 199 дорогами (з одного міста йде дорога до кожного), тоді на ремонт можна закрити 801 дорогу (1000 д. – 199 д. = 801 д.).
Відповідь: 801.
Завдання 3 (1978 р.) Точки А, В, С розміщені так, що, незалежно від вибору точки M, відрізок AM коротший від одного з відрізків BM або CM. Доведіть, що точка M належить відрізку BC.
Незалежно від вибору точки M відрізок АМ < ВМ тоді, коли точка М Є AB.
Незалежно від вибору точки M відрізок АМ < CМ тоді, коли точка М Є AC.
Відрізки АВ і АС мають спільний кінець у точці А. Вони можуть лежати на одній прямі, або на прямих, що перетинаються у точці А. У другому варіанті точка М не буде одночасно належати двом відрізкам. Отже, маємо відрізок ВС, що лежить на одній прямій.
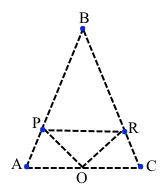
Завдання 4 (1979 р.) Розмістіть 6 точок на площині так, щоб кожні 3 з них були вершинами рівнобедреного трикутника.
Точки АВС мають утворювати рівнобедрений трикутник.
Точка О – середина відрізка АС. Прямі АС || PR.
Завдання 5 (1985 р.) Довільний трикутник розріжте на 3 частини так, щоб з них можна було скласти прямокутник.
Ділимо пополам сторони між найбільшим кутом. Від точок поділу проводимо перпендикуляри до третьої сторони. Розрізаємо трикутник по лініях перпендикулярів і складемо разом рівні сторони. Отримаємо шуканий прямокутник.
Завдання 6 (1987 р.) Чи можна квадрат розміром 6 х 6 розрізати на прямокутники розміром 1 х 4?
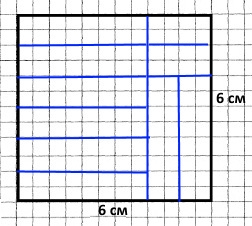
Якщо дозволено верхні справа дав прямокутники скласти до одного, тоді можна розрізати, отримаємо 9 прямокутників.
Якщо не дозволено скласти, тоді не можна, бо залишиться 2 прямокутники 1х2.