Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 15 Медіана, бісектриса і висота трикутника, властивість бісектриси рівнобедреного трикутника
Завдання 372
На малюнку 15,10 відрізок АК – висота трикутника з вершини А до сторони ВС (АК ﬩ ВС)
На малюнку 15,11 відрізок АК – бісектриса трикутника з вершини А (∠ВАК = ∠САК)
На малюнку 15,12 відрізок АК – медіана трикутника з вершини А (ВК = СК)
Завдання 373 Малюнок 15.13
1) У трикутнику ABC відрізок AT називають висотою трикутника з вершини А до сторони ВС (АТ ﬩ ВС)
2) У трикутнику ABC відрізок AN називають медіаною трикутника з вершини А до сторони ВС (BN = NC)
3) У трикутнику ABC відрізок AP називають бісектрисою трикутника з вершини А (∠BAP = ∠PAC?
Завдання 374 Малюнок 15.10
У трикутнику ABC відрізок AK – висота. Знайдіть градусні міри кутів BKA і CKA.
За умовою АК – висота до сторони ВС, тому АК ﬩ ВС, отже, ∠BKA = ∠CKA = 90°.
Відповідь: ∠BKA = ∠CKA = 90°.
Завдання 375 Малюнок 15.11
У трикутнику ABC відрізок AK – бісектриса, ∠BAK = 40°. Знайдіть градусну міру кута BAC.
За умовою АК – бісектриса, тоді ∠ВАК = 2∠ВАС, отже, ∠ВАС = ∠ВАК : 2 = 40° : 2 = 20°.
Відповідь: ∠ВАС = 20°.
Завдання 376 Малюнок 15.12
У трикутнику ABC відрізок AK – медіана, BC = 12 см. Знайдіть довжини відрізків BK і KC.
За означенням медіани АК до сторони ВС маємо ВС = ВК + КС = 2ВК, тоді ВК = КС = ВС : 2 = 12 см : 2 = 6 см.
Відповідь: ВК = КС = 6 см.
Завдання 377 Накресліть трикутник. За допомогою лінійки з поділками проведіть його медіани.
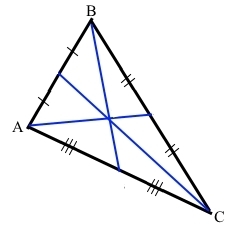
Завдання 378
Накресліть трикутник. За допомогою транспортира і лінійки проведіть його бісектриси.
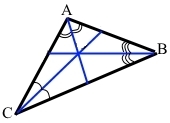
Завдання 379
Накресліть тупокутний трикутник. За допомогою креслярського косинця проведіть його висоти.
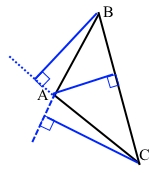
Завдання 380
Накресліть гострокутний трикутник. За допомогою креслярського косинця проведіть його висоти.
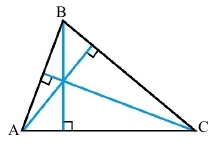
Завдання 381 Малюнок 15.14
Відрізок AK – висота рівнобедреного трикутника ABC з основою BC. Запишіть три пари рівних кутів і дві пари рівних відрізків.
∆АВС – рівнобедрений, тоді АС = АВ, ∠АСК = ∠АВК.
АК – висота до сторони СВ, АК ﬩ СВ, ∠СКА = ∠ВКА = 90°.
Для рівнобедреного трикутника висота до основи є медіаною, тому СК = КВ.
Для рівнобедреного трикутника висота до основи є бісектрисою, тому ∠САК = ∠ВАК.
Відповідь: три пари рівних кутів ∠АСК = ∠АВК, ∠СКА = ∠ВКА, ∠САК = ∠ВАК;
дві пари рівних відрізків АС = АВ, СК = КВ.
Завдання 382 Малюнок 15.14
Відрізок EP – бісектриса рівнобедреного трикутника DEF з основою DF. Запишіть три пари рівних кутів і дві пари рівних відрізків.
∆DEF – рівнобедрений, тоді DE = FE, ∠EDP = ∠EFP.
EP – висота до сторони DF, EP ﬩ DF, ∠EPD = ∠EPF = 90°.
Для рівнобедреного трикутника висота до основи є медіаною, тому DP = PF.
Для рівнобедреного трикутника висота до основи є бісектрисою, тому ∠DEP = ∠FEP.
Відповідь: три пари рівних кутів ∠EDP = ∠EFP, ∠EPD = ∠EPF, ∠DEP = ∠FEP;
дві пари рівних відрізків DE = FE, DP = PF.
Завдання 383
Не можна стверджувати, що три висоти трикутника завжди перетинаються в одній точці, оскільки теорема, яка доводиться у старших класах, стверджує, що перетинаються висоти або їхні продовження.
Завдання 384
У трикутнику ABC ∠B = ∠C. Бісектриса, проведена до якої зі сторін, є одночасно і медіаною, і висотою?
За умовою ∠B = ∠C (у рівнобедреному трикутнику кути при основі рівні), тому ВС – основа трикутника АВС. Бісектриса, проведена до основи ВС є одночасно і медіаною, і висотою.
Відповідь: до сторони ВС.
Завдання 385
1) Елементи трикутника або їхні частини сумістяться, якщо його зігнути по бісектрисі.
Для будь-якого трикутника сумістяться половини кута, з якого виходить бісектриса.
2) Елементи трикутника або їхні частини сумістяться, якщо його зігнути по висоті.
Для будь-якого трикутника сумістяться половини розгорнутого кута, який утворює сторона, до якої проведена висота.
Завдання 386
Доведіть, що коли бісектриса трикутника є його висотою, то трикутник – рівнобедрений.
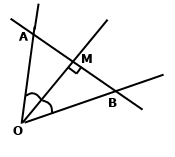
За умовою ОМ – бісектриса кута АОВ, за означенням бісектриси кута ∠ОАМ = ∠ВОМ.
За умовою ОМ – висота до сторони АВ, ОМ ﬩ АВ, тоді ∠АМО = ∠ВМО = 90°.
Розглянемо трикутники АМО і ВМО, ОМ – спільна сторона. За другою ознакою рівності трикутників (за стороною і прилеглими кутами) ∆АМО = ∆ВМО, тому ∠ОАМ = ∠ОВМ. Отже, за ознакою рівнобедреного трикутника (якщо два кути рівні, то трикутник рівнобедрений) трикутник ОАВ – рівнобедрений.
Завдання 387
Доведіть, що коли медіана трикутника є його висотою, то трикутник – рівнобедрений.
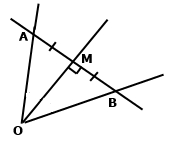
За умовою ОМ – медіана трикутника АОВ, за означенням медіани АМ = ВМ.
За умовою ОМ – висота до сторони АВ, ОМ ﬩ АВ, тоді ∠АМО = ∠ВМО = 90°.
Розглянемо трикутники АМО і ВМО, ОМ – спільна сторона. За першою ознакою рівності трикутників (за сторонами і кутом між ними) ∆АМО = ∆ВМО, тому ∠ОАМ = ∠ОВМ. Отже, за ознакою рівнобедреного трикутника (якщо два кути рівні, то трикутник рівнобедрений) трикутник ОАВ – рівнобедрений.
Завдання 388
AD і A1D1 – відповідно бісектриси рівних трикутників ABC і A1B1C1. Доведіть, що ∆ADC = ∆A1D1C1.
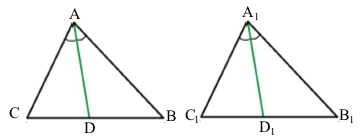
За умовою ∆АВС = ∆А1В1С1, тому ∠САВ = ∠С1А1В1, ∠АСВ = ∠А1С1В1, СА = С1А1.
За умовою AD і A1D1 – відповідно бісектриси трикутників, тому ∠САВ = 2∠САD, ∠С1А1В1 = 2∠С1А1D1, оскільки ліві частини рівні, тоді праві також рівні, тому ∠САD = ∠C1A1D1. Виконується друга ознака рівності трикутників (за стороною і прилеглими кутами), отже, ∆ADC = ∆А1D1С1.
Завдання 389
Доведіть, що в рівнобедреному трикутнику медіани, проведені до бічних сторін, – рівні.
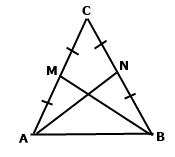
За умовою трикутник АСВ – рівнобедрений, ∠САВ = ∠СВА, АС = ВС.
За умовою ВМ – медіана до бічної сторони АС, тоді АМ = МС, тобто АС = 2АМ.
За умовою AN – медіана до бічної сторони СВ, тоді CN = NB, тобто СВ = 2NB.
Оскільки АС = ВС, тоді рівні праві частини АМ = NB.
Для трикутників АМВ і BNA сторона АВ – спільна. За першою ознакою рівності трикутників (за сторонами і кутом між ними) ∆АМВ = ∆BNA. Отже, медіани до бічних сторін МВ = NA.
Завдання 390
Доведіть, що в рівнобедреному трикутнику бісектриси, проведені до бічних сторін, – рівні.
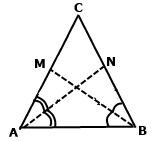
За умовою трикутник АСВ – рівнобедрений, ∠САВ = ∠СВА, АС = ВС.
За умовою ВМ – медіана до бічної сторони АС, тоді АМ = МС, тобто АС = 2АМ.
За умовою AN – медіана до бічної сторони СВ, тоді CN = NB, тобто СВ = 2NB.
Оскільки АС = ВС, тоді рівні праві частини АМ = NB.
Для трикутників АМВ і BNA сторона АВ – спільна. За першою ознакою рівності трикутників (за сторонами і кутом між ними) ∆АМВ = ∆BNA. Отже, медіани до бічних сторін МВ = NA.
Завдання 391
У рівнобедреному трикутнику ABC з основою AC проведено висоту BD. Знайдіть периметр трикутника ABC, якщо BD = 10 см, а периметр трикутника ABD дорівнює 40 см.
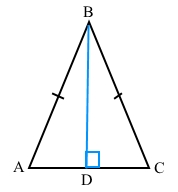
У рівнобедреному трикутнику АВС, висота BD – є медіаною, AD = DC, AD + DC = AC.
2РABD = АВ + AD + BD + BD + DC + BC,
2РABD = АВ + AC + BC + 2BD,
2РABD = РABC + 2BD
РABC = 2РABD – 2BD = 2 • (РABD – BD) = 2 • (40 – 10) = 60 (см)
Відповідь: РАВС = 60 см.
Завдання 392
У рівнобедреному трикутнику ABC з основою AB проведено медіану CK. Знайдіть її довжину, якщо периметр трикутника ACK дорівнює 12 см, а периметр трикутника ABC – 16 см.
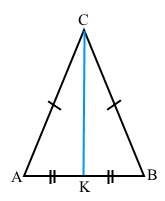
Трикутник АВС – рівнобедрений, бічні сторони АС = ВС.
СК – медіана до основи АВ, тому АК = КВ, або АВ = АК + КВ.
2PАСК = АС + АК + СК + СК + СВ + КВ = (АС + СВ) + (АК + КВ) + 2СК
2PАСК = АС + СВ + АВ + 2СК
2PАСК = PАВС + 2СК
2СК = 2PАСК – PАВС = 2 • 12 – 16 = 8 (см)
СК = 8 : 2 = 4 (см)
Відповідь: СК = 4 см
Завдання 393
Доведіть, що коли медіана трикутника є його бісектрисою, то трикутник – рівнобедрений.
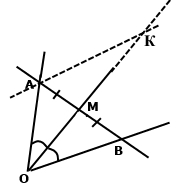
Продовжимо медіану і відкладемо відрізок МК = ОМ.
За умовою ОМ – медіана з кута АОВ до сторони АВ, за означенням АМ = МВ.
За умовою ОМ – бісектриса кута АОВ до сторони АВ, за означенням ∠МОВ = ∠МОА.
Вертикальні кути АМК = ВМО, за першою ознакою рівності трикутників ∆АМК = ∆ВМО, тому АК = ОВ, ∠МОВ = ∠МКА.
За умовою ОМ = МК, МА – спільна сторона трикутників ОМА і КМА, ∠МОА = ∠МКА.
За другою ознакою рівності трикутників ∆ОМА = ∆КМА, тоді ОА = АК = ОВ. У трикутника АОВ рівні сторони ОА = ОВ, отже, за означенням трикутник рівнобедрений.
Завдання 394
Два з восьми кутів, що утворилися при перетині прямих a і b січною c, дорівнюють 30° і 140°. Чи можуть прямі a і b бути паралельними?
Припустимо, що прямі а і b паралельні. При перетині паралельних прямих січною утворюється по 4 рівних кути. Кути різних пар утворюють внутрішні односторонні кути, сума яких дорівнює 180°. Оскільки 140° + 130° < 180°, то не виконується ознака паралельності прямих а і b при перетині січною c. Отже, прямі а і b ніколи не можуть бути паралельними.
Завдання 395
Периметр рівностороннього трикутника дорівнює 12 см. На його стороні побудували рівнобедрений трикутник так, що сторона даного трикутника є основою рівнобедреного. Знайдіть сторони рівнобедреного трикутника, якщо його периметр 18 см.
Розв’язання
1) 12 : 3 = 4 (см) – довжина основи рівнобедреного трикутника (сторона рівностороннього трикутника).
2) 18 – 4 = 14 (см) – сума бічних сторін рівнобедреного трикутника.
3) 14 : 2 = 7 (см) – бічна сторона рівнобедреного трикутника.
Відповідь: основа 4 см, бічні сторони по 7 см.
Завдання 396
Знайдіть сторони рівнобедреного трикутника, периметр якого – 69 см, а його основа складає 30% від бічної сторони.
Нехай х (см) – бічна сторона, тоді 0,3х (см) – основа. Складемо рівняння для знаходження периметра рівнобедреного трикутника.
2х + 0,3х = 69
2,3х = 69
х = 69 : 2,3
х = 30 см – бічна сторона.
0,3х = 30 • 0,3 = 9 (см) – основа трикутника.
Відповідь: основа 9 см, бічні сторони по 30 см.
Життєва математика
Завдання 397
Визначте суму грошей, яку потрібно сплатити за фарбування тренажерного залу, ширина, довжина і висота якого – 9,4 м, 6,5 м, 3,2 м. Фарбування одного квадратного метра коштує 25 грн. Вікна та двері складають 9% від загальної площі стін. Округліть до десятків гривень.
a — 6,5 м
b — 9,4 м
h — 3,2 м
1) ah + ah + bh + bh = 2ah + 2bh = 2h (а + b) = 3,2 • 2 • (6,5 + 9,4) = 101,76 (м2) – площа стін із вікнами і дверми.
2) 101,76 : 100 • 91 = 92,6016 (м2) – площа самих стін.
3) ab = 6,5 • 9,4 = 61,1 (м2) – площа стелі.
4) 92,6016 + 61,1 = 153,7016 (м2) – загальна площа.
1 м2 — 25 грн
153,7016 м2 — ? грн
5) 25 • 153, 7016 = 3842,54 (грн) ≈ 3840 (грн)
Відповідь: потрібно сплатити 3840 гривень.
Завдання 398 Олесь придбав акваріум у формі куба, що вміщує 125 л води. Він наповнив акваріум, не доливши до краю 6 см. Скільки літрів води Олесь налив у акваріум?
1 л води = 1 дм3, 125 л = 125 дм3.
125 = 53, тому ребро акваріума у формі куба 5 дм.
5 дм – 6 см = 50 см – 6 см = 44 см – висота води в акваріумі.
Виміри для знаходження об’єму а = 5 дм = 50 см, b = 5 дм = 50 см, h = 44 см.
V = abh = 50 • 50 • 44 = 110 000 (см3) = 110 (л)
110 000 см3 = 110 • 10 см • 10 см • 10 см = 110 • 1 дм • 1 дм • 1 дм = 110 дм3 = 100 л
Відповідь: V = 110 л.