Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 17 Сума кутів трикутника
Завдання 417
Дано ∆PLK. Знайдіть значення суми ∠P + ∠L + ∠K.
За теоремою про суму кутів трикутника ∠P + ∠L + ∠K = 180°.
Завдання 418
1) Чи існує трикутник з кутами 30°, 60° і 70°?
Знайдемо суму кутів 30° + 60° + 70° = 160°. Не існує такого трикутника.
2) Чи існує трикутник з кутами 70°, 40° і 70°?
Знайдемо суму кутів 70° + 40° + 70° = 180°. Такий трикутник існує.
Завдання 419
1) Чи існує трикутник з кутами 50°, 70° і 80°?
Знайдемо суму кутів 50° + 70° + 80° = 200°. Не існує такого трикутника.
2) Чи існує трикутник з кутами 30°, 60° і 90°?
Знайдемо суму кутів 30° + 60° + 90° = 180°. Такий трикутник існує.
Завдання 420
1) Знайдіть третій кут трикутника, якщо два його кути дорівнюють 43° і 54°.
За теоремою про суму кутів трикутника знайдемо третій кут 180° – 43° – 54° = 83°.
Відповідь: 83°.
2) Знайдіть третій кут трикутника, якщо два його кути дорівнюють 9° і 93°.
За теоремою про суму кутів трикутника знайдемо третій кут 180° – 9° – 93° = 78°.
Відповідь: 78°.
3) Знайдіть третій кут трикутника, якщо два його кути дорівнюють 83° і 89°.
За теоремою про суму кутів трикутника знайдемо третій кут 180° – 83° – 89° = 8°.
Відповідь: 8°.
Завдання 421
1) Знайдіть третій кут трикутника, якщо два його кути дорівнюють 15° і 38°.
За теоремою про суму кутів трикутника знайдемо третій кут 180° – 15° – 38° = 127°.
Відповідь: 127°.
2) Знайдіть третій кут трикутника, якщо два його кути дорівнюють 28° і 105°.
За теоремою про суму кутів трикутника знайдемо третій кут 180° – 28° – 105° = 47°.
Відповідь: 47°.
3) Знайдіть третій кут трикутника, якщо два його кути дорівнюють 7° і 91°.
За теоремою про суму кутів трикутника знайдемо третій кут 180° – 7° – 91° = 82°.
Відповідь: 82°.
Завдання 422
1) якщо один з кутів трикутника тупий, то інші гострі;
2) якщо один з кутів трикутника прямий, то інші гострі.
Завдання 423
Сума двох кутів трикутника дорівнює 126°. Знайдіть третій кут трикутника.
За теоремою про суму кутів трикутника знайдемо третій кут 180° – 126° = 54°.
Відповідь: 54°.
Завдання 424
У трикутнику ABC ∠A + ∠B = 58°. Знайдіть ∠C.
За теоремою про суму кутів трикутника ∠А + ∠В + ∠С = 180°.
Знайдемо ∠С = 180° – (∠А + ∠В) = 180° – 58° = 122°.
Відповідь: ∠С = 122°.
Завдання 425
Один з кутів трикутника дорівнює 62°. Знайдіть суму градусних мір двох інших кутів.
За теоремою про суму кутів трикутника 180° – 62° = 118° – сума двох інших кутів.
Завдання 426
Доведіть, що кожний з кутів рівностороннього трикутника дорівнює 60°.
За умовою трикутник рівносторонній, тоді його кути рівні. За теоремою сума кутів трикутника дорівнює 180°. Звідси 180° : 3 = 60°. Отже, кожний з кутів рівностороннього трикутника дорівнює 60°.
Відповідь: 60°, 60°, 60°.
Завдання 427
Кут при основі рівнобедреного трикутника дорівнює 70°. Знайдіть кут при вершині перетину бічних сторін.
70° + 70° = 140° – сума кутів при основі. За теоремою про суму кутів трикутника 180° – 140° = 40° – кут при вершині перетину бічних сторін.
Відповідь: 40°.
Завдання 428
Знайдіть кут при вершині рівнобедреного трикутника, якщо кут при основі дорівнює 45°.
45° + 45° = 90° – сума кутів при основі. За теоремою про суму кутів трикутника 180° – 90° = 90° – кут при вершині перетину бічних сторін.
Відповідь: 90°.
Завдання 429
Знайдіть кути при основі рівнобедреного трикутника, якщо кут при вершині дорівнює 80°.
За теоремою про суму кутів трикутника 180° – 80° = 100° – сума кутів при основі. Трикутник рівнобедрений, тому його кути при основі рівні. 100° : 2 = 50° – градусна міра кожного кута при основі.
Відповідь: 50°, 50°.
Завдання 430
Кут при вершині рівнобедреного трикутника дорівнює 50°. Знайдіть кути при основі.
За теоремою про суму кутів трикутника 180° – 50° = 130° – сума кутів при основі. Трикутник рівнобедрений, тому його кути при основі рівні. 130° : 2 = 65° – градусна міра кожного кута при основі.
Відповідь: 65°, 65°.
Завдання 431
1) Знайдіть невідомі кути трикутника ABC на малюнку 17.1.
За теоремою вертикальних кутів (вертикальні кути рівні) ∠СВА = 70°. За теоремою про суму кутів трикутника ∠А = 180° – 80° – 70° = 30°.
Відповідь: 70°, 30°.
2) Знайдіть невідомі кути трикутника ABC на малюнку 17.2.
За теоремою суміжних кутів (сума суміжних кутів дорівнює 180°) ∠АСВ = 180° – 135° = 45°. За теоремою про суму кутів трикутника ∠В = 180° – (75° + 45°) = 60°.
Відповідь: 45°, 60°.
Завдання 432
1) Знайдіть невідомі кути трикутника MNL на малюнку 17.3.
За теоремою вертикальних кутів (вертикальні кути рівні) ∠LMN = 50°. За теоремою про суму кутів трикутника ∠LNM = 180° – (70° + 50°) = 60°.
Відповідь: 50°, 60°.
2) Знайдіть невідомі кути трикутника MNL на малюнку 17.4.
За теоремою суміжних кутів (сума суміжних кутів дорівнює 180°) ∠NML = 180° – 140° = 40°. За теоремою про суму кутів трикутника ∠MNL = 180° – (40° + 50°) = 90°.
Відповідь: 40°, 90°.
Завдання 433 Малюнок 17.5
У трикутнику ABC проведено бісектрису CP. Знайдіть ∠PCB, якщо ∠A = 50°, ∠B = 70°.
За теоремою про суму кутів трикутника АВС маємо ∠АСВ = 180° – (50° + 70°) = 60°.
СР – бісектриса кута, тоді ∠АСВ = 2∠РСВ, звідки ∠РСВ = ∠АСВ : 2 = 60° : 2 = 30°.
Відповідь: 30°.
Завдання 434 Малюнок 17.5
У трикутнику ABC проведено бісектрису CP. Знайдіть ∠A, якщо ∠B = 65°, ∠ACP = 40°.
СР – бісектриса кута, тоді ∠АСВ = 2∠АСР = 40° • 2 = 80°.
За теоремою про суму кутів трикутника АВС маємо ∠А = 180° – (65° + 80°) = 35°.
Відповідь: 35°.
Завдання 435
Знайдіть кути трикутника MNL, якщо ∠M + ∠N = 120°, ∠M + ∠L = 140°.
За теоремою про суму кутів трикутника MNL відомо, що ∠М + ∠N + ∠L = 180°.
Тепер знайдемо суму таких кутів ∠М + ∠N + ∠M + ∠L = 120° + 140° = 260°. З іншої сторони ∠М + ∠N + ∠M + ∠L = (∠М + ∠N + ∠L) + ∠М = 180° + ∠М. Якщо рівні ліві частини, тоді рівні праві частини, тому 260° = 180° + ∠М, тоді ∠М = 260° – 180° = 80°.
∠N = 120° – ∠М = 120° – 80° = 40°,
∠L = 140° – ∠М = 140° – 80° = 60°.
Відповідь: ∠М = 80°, ∠N = 40°, ∠L = 60°.
Завдання 436
Знайдіть кути трикутника ABC, якщо ∠A + ∠B = 100°, ∠A + ∠C = 130°.
За теоремою про суму кутів трикутника АВС відомо, що ∠А + ∠В + ∠С = 180°.
Тепер знайдемо суму таких кутів ∠А + ∠В + ∠А + ∠С = 100° + 130° = 230°. З іншої сторони ∠А + ∠В + ∠А + ∠С = (∠А + ∠В + ∠С) + ∠А = 180° + ∠А. Якщо рівні ліві частини, тоді рівні праві частини, тому 230° = 180° + ∠А, тоді ∠А = 230° – 180° = 50°.
∠В = 100° – ∠А = 100° – 50° = 50°,
∠С = 130° – ∠А = 130° – 50° = 80°.
Відповідь: ∠А = 50°, ∠В = 50°, ∠С = 80°.
Завдання 437
Доведіть, що в кожному трикутнику є кут, не менший від 60° (більший або рівний 60°).
У рівносторонньому трикутнику кути дорівнюють 60°. Для інших трикутників припустимо, що нема кута більшого за 60°. Якщо всі кути менші за 60°, тоді їхня сума не дорівнює 180°, що суперечить теоремі про суму кутів трикутника. Тому наше припущення невірне. Отже, в кожному трикутнику є кут, не менший від 60° (більший або рівний 60°).
Завдання 438
Доведіть, що в кожному трикутнику є кут, не більший за 60° (менший або рівний 60°)
У рівносторонньому трикутнику кути дорівнюють 60°. Для інших трикутників припустимо, що нема кута меншого за 60°. Якщо всі кути перевищують 60°, тоді їхня сума перевищує 180°, що суперечить теоремі про суму кутів трикутника. Тому наше припущення невірне. Отже, в кожному трикутнику є кут, не більший за 60° (менший або рівний 60°).
Завдання 439
У трикутнику ABC ∠A : ∠B : ∠C = 3 : 4 : 5. Знайдіть ці кути.
За теоремою про суму кутів трикутника АВС маємо рівність ∠A + ∠B + ∠C = 180°.
Нехай х (°) – градусна міра одної частини, тоді 3х (°) – градусна міра кут А, 4х (°) – градусна міра кута В, 5х (°) – градусна міра кута С. Складемо рівняння.
3х + 4х + 5х = 180
12х = 180
х = 180 : 12
х = 180 : 6 : 2
х = 15 (°) – градусна міра частини.
3х = 15 • 3 = 45 (°) – ∠A.
4х = 15 • 4 = 60 (°) – ∠В.
5х = 15 • 5 = 75 (°) – ∠С.
Відповідь: ∠A = 45°, ∠В = 60°, ∠С = 75°
Завдання 440
Знайдіть градусні міри кутів трикутника, якщо вони відносяться як 2 : 3 : 5.
За теоремою про суму кутів трикутника 180°.
Нехай х (°) – градусна міра одної частини, тоді 2х (°) – градусна міра І кута, 3х (°) – а міра ІІ кута, 5х (°) – градусна міра ІІІ кута. Складемо рівняння.
2х + 3х + 5х = 180
10х = 180
х = 180 : 10
х = 18 (°) – градусна міра частини.
2х = 18 • 2 = (10 + 8) • 2 = 36 (°) – градусна міра І кута.
3х = 18 • 3 = (10 + 8) • 3 = 54 (°) – градусна міра ІІ кута.
5х = 18 • 5 = (10 + 8) • 5 = 90 (°) – градусна міра ІІІ кута.
Відповідь: 36°, 54°, 90°
Завдання 441
Знайдіть кути рівнобедреного трикутника, якщо кут при основі на 15° більший за кут при вершині.
За теоремою про рівнобедрений трикутник його кути при основі рівні.
За теоремою сума кутів трикутника дорівнює 180°.
Нехай х (°) – кут при вершині, тоді х + 15 (°) – кут при основі. Складемо рівняння
х + х + 15 + х + 15 = 180
3х + 30 = 180
3х = 180 – 30
3х = 150
х = 150 : 3
х = 50 (°) – градусна міра кута при вершині.
х + 15 = 50 + 15 = 65 (°) – градусна міра кута при основі.
Відповідь: 65°, 65°, 50°.
Завдання 442
Знайдіть кути рівнобедреного трикутника, якщо кут при вершині на 24° більший за кут при основі.
За теоремою про рівнобедрений трикутник його кути при основі рівні.
За теоремою сума кутів трикутника дорівнює 180°.
Нехай х (°) – кут при основі, тоді х + 24 (°) – кут при вершині. Складемо рівняння
х + 24 + х + х = 180
3х + 24 = 180
3х = 180 – 24
3х = 156
х = 156 : 3 = (150 + 6) : 3 = 52 (°) – градусна міра кута при основі.
х + 24 = 52 + 24 = 76 (°) – градусна міра кута при вершині.
Відповідь: 52°, 52°, 76°.
Завдання 443
Доведіть, що кути при основі рівнобедреного трикутника гострі.
Згідно наслідку теореми про суму кутів трикутника трикутник не може мати більше, ніж один кут прямий або тупий. За умовою трикутник рівнобедрений, тому він має принаймні два однакових кути. Отже, кути при основі гострі.
Завдання 444
Якщо один з кутів рівнобедреного трикутника дорівнює 60°, то трикутник – рівносторонній. Доведіть це твердження. (Розгляньте два випадки.)
І випадок. Нехай кут при вершині дорівнює 60°, тоді за теоремою про суму кутів трикутника на кути при основі припадає 180° – 60° = 120°. У рівнобедреного трикутника кути при основі рівні, вони дорівнюють, тому 120 : 2 = 60°. У трикутника рівні кути. Отже, такий трикутник рівносторонній (за наслідком з теореми про ознаку рівнобедреного трикутника).
ІІ випадок. Нехай кут при основі дорівнює 60°. У рівнобедреного трикутника кути при основі рівні. Із теореми про суму кутів трикутника на третій кут при вершині 180° – (60° + 60°) = 60°. У трикутника рівні кути. Отже, такий трикутник рівносторонній (за наслідком з теореми про ознаку рівнобедреного трикутника).
Завдання 445
1) У ∆ABC ∠A = 80°. Визначте градусні міри кутів B і C, якщо кут B на 14° більший за кут C.
Сума кутів трикутника дорівнює 180°.
Нехай х (°) – кут С, тоді х + 14 (°) – кут В. Складемо рівняння.
80 + (х + 14) + х = 180
94 + 2х = 180
2х = 180 – 94
2х = 86
х = 86 : 2 = 43 (°) – кут С (Ь).
х + 14 = 43 + 14 = 57 (°) – кут В (О).
2) У ∆ABC ∠A = 80°. Визначте градусні міри кутів B і C, якщо кут B у 3 рази менший від кута C.
Сума кутів трикутника дорівнює 180°.
Нехай х (°) – кут В, тоді 3х (°) – кут С. Складемо рівняння.
80 + х + 3х = 180
80 + 4х = 180
4х = 180 – 80
4х = 100
х = 100 : 4 = (80 + 20) : 4 = 25 (°) – кут В (1 частина) (Л).
3х = 25 • 3 = 75 (°) – кут С (3 частини) (К).
3) У ∆ABC ∠A = 80°. Визначте градусні міри кутів B і C, якщо кут ∠B : ∠C = 2 : 3.
Сума кутів трикутника дорівнює 180°.
Нехай х (°) – градусна міра частини кутів, тоді 2х (°) – кут В, 3х (°) – кут С. Складемо рівняння.
80 + 2х + 3х = 180
80 + 5х = 180
5х = 180 – 80
5х = 100
х = 100 : 5 = 20 (°) – градусна міра частини кутів.
2х = 20 • 2 = 40 (°) – кут В (2 частини) (В).
3х = 20 • 3 = 60 (°) – кут С (3 частини) (Р).
Прізвище видатного українського вченого в галузі ракетобудування та космонавтики:
|
75° |
57° |
60° |
57° |
25° |
43° |
57° |
40° |
|
К |
О |
Р |
О |
Л |
Ь |
О |
В |
Дізнайтеся з Інтернету про його біографію та наукові досягнення…
Завдання 446
Один з кутів трикутника вдвічі більший за другий. Знайдіть ці кути, якщо третій кут дорівнює 36°.
Сума кутів трикутника дорівнює 180°.
Нехай х (°) – перший кут, тоді 2х (°) – другий кут. Складемо рівняння.
х + 2х + 36 = 180
3х + 36 = 180
3х = 180 – 36
3х = 144
х = 144 : 3 = (120 + 24) : 3 = 48 (°) – перший кут.
2х = 48 • 2 = 48 + 48 = 96 (°) – другий кут.
Відповідь: 48°, 96°.
Завдання 447 Малюнок 17.6
AB = DC, ∠B = ∠C. Доведіть, що ∆AOB = ∆DOC.
Вертикальні кути рівні ∠AOB = ∠DOC. За теоремою про суму сторін трикутника можна записати ∠А + ∠В + ∠АОВ = ∠D + ∠C + ∠DOC. = 180°. За умовою ∠B = ∠C., тоді
∠А + ∠В + ∠АОВ = ∠D + ∠C + ∠DOC, ∠А = ∠D + (∠C – ∠В) + (∠DOC – ∠АОВ.) = ∠D. Отже, ∆AOB = ∆DOC за другою ознакою рівності трикутників (за стороною і прилеглими кутами).
Завдання 448
Доведіть рівність трикутників ABC і A1B1C1, якщо BC = B1C1, ∠A = ∠A1, ∠B = ∠B1.
За умовою ∠A = ∠A1, ∠B = ∠B1. За теоремою про суму кутів трикутника ∠A + ∠В + ∠С = 180°, ∠А1 + ∠В1 + ∠С1 = 180°, рівні праві частини рівності, тому рівні ліві частини рівності.
∠С = ∠С1. За умовою BC = B1C1 і рівні кути прилеглі кути ∠B = ∠B1. і ∠С = ∠С1. Отже, ABC і A1B1C1 за другою ознакою рівності трикутників (за стороною і прилеглими кутами).
Завдання 449
У трикутнику два кути дорівнюють 46° і 64°. Знайдіть кут між прямими, на яких лежать бісектриси цих кутів.
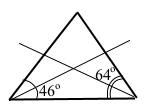
Бісектриса кута ділить його пополам, маємо кут між одною бісектрисою і спільною стороною трикутника 46° : 2 = 23°, між другою бісектрисою і спільною стороною трикутника 64° : 2 = 32°. Згідно теореми про суму сторін трикутника 180° – (23° + 32°) = 125° – більший вертикальний кут. Вертикальні кути різної пари є суміжними, тому 180 – 125 = 55° – кут між прямими, на яких лежать бісектриси цих кутів (менший із вертикальних кутів між прямими).
Відповідь: 55°.
Завдання 450
У трикутнику два кути дорівнюють 70° і 80°. Знайдіть кут між прямими, на яких лежать висоти цих кутів.
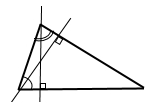
Згідно теореми про суму кутів трикутника можна знайти градусну міру кута між висотою і стороною трикутника, що перетинаються у спільній точці – вершині трикутника. Для кожної висоти маємо 180° – 90° – 70° = 20°, 180° – 90° – 80° = 10°.
Один із вертикальних кутів між прямими, на яких лежать висоти цих кутів, за теоремою про суму кутів трикутника дорівнює 180° – 20° – 10° = 150°. Вертикальні кути різної пари є суміжними, за теоремою про суміжні кути 180° – 150° = 30° – шуканий кут між прямими (менший із вертикальних кутів), на яких лежать висоти цих кутів.
Відповідь: 30°.
Завдання 451
1) Знайдіть кути рівнобедреного трикутника, якщо один з них дорівнює 12°.
І випадок. Кут між бічними сторонами трикутника (при вершині трикутника) дорівнює 12°. У рівнобедреному трикутнику кути при основі рівні. Сума кутів трикутника дорівнює 180°.
Нехай х (°) – прилеглий до основи кут трикутника. Складемо рівняння.
х + х + 12 = 180
2х = 180 – 12
2х = 168
х = 168 : 2 = 84 (°) – градусна міра прилеглого до основи кута.
Відповідь: 84°, 84°, 12°
ІІ випадок. Прилеглий до основи кут трикутника 12°. У рівнобедреному трикутнику кути при основі рівні. Сума кутів трикутника дорівнює 180°.
Нехай х (°) – кут при вершині рівнобедреного трикутника. Складемо рівняння.
х + 12 + 12 = 180
х + 24 = 180
х = 180 – 24
х = 156 (°) – градусна міра кута при вершині рівнобедреного трикутника.
Відповідь: 12°, 12°, 156°.
2) Знайдіть кути рівнобедреного трикутника, якщо один з них дорівнює 92°.
Кут між бічними сторонами трикутника (при вершині трикутника) дорівнює 92°. У рівнобедреному трикутнику кути при основі рівні. Сума кутів трикутника дорівнює 180°.
Нехай х (°) – прилеглий до основи кут трикутника. Складемо рівняння.
х + х + 92 = 180
2х = 180 – 92
2х = 88
х = 88 : 2 = 44 (°) – градусна міра прилеглого до основи кута.
Відповідь: 44°, 44°, 92°
Примітка. Для другого випадку не виконується теорема про суму сторін трикутника, тому розглядаємо тільки один випадок.
Завдання 452
1) Знайдіть кути рівнобедреного трикутника, якщо один з них дорівнює 28°.
І випадок. Кут між бічними сторонами трикутника (при вершині трикутника) дорівнює 28°. У рівнобедреному трикутнику кути при основі рівні. Сума кутів трикутника дорівнює 180°.
Нехай х (°) – прилеглий до основи кут трикутника. Складемо рівняння.
х + х + 28 = 180
2х = 180 – 28
2х = 152
х = 152 : 2 = (140 + 12) : 2 = 76 (°) – градусна міра прилеглого до основи кута.
Відповідь: 76°, 76°, 28°
ІІ випадок. Прилеглий до основи кут трикутника 28°. У рівнобедреному трикутнику кути при основі рівні. Сума кутів трикутника дорівнює 180°.
Нехай х (°) – кут при вершині рівнобедреного трикутника. Складемо рівняння.
х + 28 + 28 = 180
х + 56 = 180
х = 180 – 56
х = 124 (°) – градусна міра кута при вершині рівнобедреного трикутника.
Відповідь: 28°, 28°, 124°.
2) Знайдіть кути рівнобедреного трикутника, якщо один з них дорівнює 106°.
Кут між бічними сторонами трикутника (при вершині трикутника) дорівнює 106°. У рівнобедреному трикутнику кути при основі рівні. Сума кутів трикутника дорівнює 180°.
Нехай х (°) – прилеглий до основи кут трикутника. Складемо рівняння.
х + х + 106 = 180
2х = 180 – 106
2х = 74
х = 74 : 2 = (60 + 14) : 2 = 37 (°) – градусна міра прилеглого до основи кута.
Відповідь: 37°, 37°, 106°
Примітка. Для другого випадку не виконується теорема про суму сторін трикутника, тому розглядаємо тільки один випадок.
Завдання 453
Доведіть, що бісектриси двох внутрішніх односторонніх кутів при двох паралельних прямих і січній перетинаються під прямим кутом.
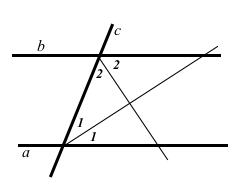
Бісектриси двох внутрішніх односторонніх кутів ділять їх пополам. За умовою а || b, с – січна. За властивістю внутрішніх односторонніх кутів знайдемо суму внутрішніх односторонніх кутів. ∠1 + ∠1 + ∠2 + ∠2 = 180°, (∠1 + ∠2) • 2 = 180°, ∠1 + ∠2 = 180° : 2 = 90°. Згідно теореми про суму кутів трикутника знайдемо кут між бісектрисами 180° – 90° = 90°. Отже, бісектриси двох внутрішніх односторонніх кутів при двох паралельних прямих і січній перетинаються під прямим кутом.
Завдання 454
Знайдіть кути рівнобедреного трикутника, якщо один з них удвічі більший за інший. Скільки випадків слід розглянути?
І випадок. У рівнобедреному трикутнику кути при основі рівні. Сума кутів трикутника дорівнює 180°.
Нехай х (°) – прилеглий до основи кут трикутника, тоді 2х (°) – кут при вершині. Складемо рівняння.
х + х + 2х = 180
4х = 180
х = 180 : 4 = (160 + 20) : 4 = 45 (°) – градусна міра прилеглого до основи кута.
2х = 45 • 2 = 45 + 45 = 90 (°) – градусна міра кута при вершині рівнобедреного трикутника.
Відповідь: 45°, 45°, 90°
ІІ випадок. У рівнобедреному трикутнику кути при основі рівні. Сума кутів трикутника дорівнює 180°.
Нехай х (°) – градусна міра кута при вершині рівнобедреного трикутника, тоді 2х (°) – градусна міра кута при основі. Складемо рівняння.
х + 2х + 2х = 180
5х = 180
х = 180 : 5 = (150 + 30) : 5 = 36 (°) – градусна міра прилеглого до основи кута.
2х = 36 • 2 = 36 + 36 = 72 (°) – градусна міра кута при вершині рівнобедреного трикутника.
Відповідь: 36°, 36°, 72°
Завдання 455
Знайдіть кути рівнобедреного трикутника, якщо один з них на 15° більший за інший. Скільки випадків слід розглянути?
І випадок. У рівнобедреному трикутнику кути при основі рівні. Сума кутів трикутника дорівнює 180°.
Нехай х (°) – прилеглий до основи кут трикутника, тоді х + 15 (°) – кут при вершині. Складемо рівняння.
х + х + (х + 15) = 180
3х + 15 = 180
3х = 180 – 15
3х = 165
х = 165 : 3 = (150 + 15) : 3 = 55 (°) – градусна міра прилеглого до основи кута.
х + 15 = 55 + 15 = 70 (°) – градусна міра кута при вершині рівнобедреного трикутника.
Відповідь: 55°, 55°, 70°
ІІ випадок. У рівнобедреному трикутнику кути при основі рівні. Сума кутів трикутника дорівнює 180°.
Нехай х (°) – градусна міра кута при вершині рівнобедреного трикутника, тоді х + 15 (°) – градусна міра кута при основі. Складемо рівняння.
х + (х + 15) + (х + 15) = 180
3х + 30 = 180
3х = 180 – 30
3х = 150
х = 150 : 3 = 50 (°) – градусна міра кута при вершині рівнобедреного трикутника.
х + 15 = 50 + 15 = 65 (°) – градусна міра кути при основі.
Відповідь: 65°, 65°, 50°
Завдання 456
Кут при основі рівнобедреного трикутника дорівнює 72°, а бісектриса кута при основі цього трикутника – 5 см. Знайдіть основу трикутника.
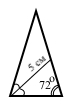
У рівнобедреному трикутнику при основі кути рівні. Бісектриса ділить кут пополам, тому кут між бісектрисою і основою трикутника 72 : 2 = 36°. Згідно теореми про суму кутів трикутника маємо кут між бісектрисою і бічною стороною заданого трикутника 180° – 72° – 36° = 72°. Утворений трикутник рівнобедрений за ознакою про рівнобедрений трикутник (якщо два кути рівні, тоді трикутник рівнобедрений), тому бісектриса і основа – рівні.
Відповідь: 5 см.
Вправи для повторення
Завдання 457
Точка K лежить між точками P і L. Знайдіть PK, якщо PL = 56 мм, а KL = 3 см 4 мм.
За властивістю вимірювання відрізків PL = PK + KL, звідси РК = PL – KL = 56 мм – 3 см 4 мм = 56 мм – 34 мм = 22 мм = 2 см 2 мм
Відповідь: РК = 2 см 2 мм.
Завдання 458
Дано ∠1 = ∠2. Доведіть, що m || n.
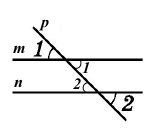
За умовою ∠1 = ∠2, оскільки вертикальні кути рівні, тому рівні внутрішні різносторонні кути, які утворюють прямі m і n із січною Р. Отже, за ознакою паралельних прямих m || n.
Завдання 459
∠AOB = 40°, ∠AOC = 60°. Знайдіть ∠BOC. Скільки випадків слід розглянути?
І випадок. Промінь ОВ проходить між сторонами кута АОС. За властивістю вимірювання кутів ∠АОС = ∠АОВ + ∠ВОС, звідси ∠ВОС = ∠АОС – ∠АОВ = 60° – 40° = 20°.
ІІ випадок. Промінь ОА проходить між сторонами кута ВОС. За властивістю вимірювання кутів ∠ВОС = ∠ВОА + ∠АОС, = ∠АОВ + ∠АОС = 60° + 40° = 100°.
Відповідь: ВОС = 20° або ∠ВОС = 100°.
Завдання 460
Трикутники ABC і ABD – рівносторонні. Доведіть, що AB ﬩ CD.
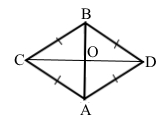
За умовою трикутники ABC і ABD – рівносторонні, тоді у кожного рівностороннього трикутника три кути рівні і дорівнюють 60°, сторони АВ = ВС = АС, АВ = BD = FD, звідси АВ = ВС = АС = BD = FD, ∆ABC = ∆ABD за третьою ознакою рівності трикутників (за трьома сторонами). За властивістю вимірювання кутів ∠CBD = ∠CBA + ∠ABD = 60° + 60° = 120°. За означенням трикутник CBD – рівнобедрений, тоді його кути при основі рівні ∠BCD = ∠BDC. Згідно теореми про суму кутів трикутника ∠BCD = ∠BCO = (180° – ∠CBD) : 2 = (180° – 120°) : 2 = 30°. Розглянемо трикутник СОВ. Згідно теореми про суму кутів трикутника кут ∠СОВ = 180° – (30° + 60°) = 90°. Цей кут буде шуканим кутом між відрізками CD і ВС. Отже, AB ﬩ CD.
Життєва математика
Завдання 461
На центральну міську клумбу, що має форму прямокутника зі сторонами 20 м та 6 м, потрібно висадити цибулини тюльпанів з розрахунку 60 цибулин на 1 м2.
1) Скільки цибулин потрібно заготувати для висаджування?
Короткий запис
60 ц. — 1 м2
? ц. — S м2
1) 20 • 6 = 120 (м2) – площа клумби.
2) 120 • 60 = (100 + 20) • 60 = 7200 (ц.) – цибулин потрібно.
2) Тюльпани продають в упаковках по 3 цибулини. Ціна такої упаковки 28 грн. Магазин готовий зробити знижки міській адміністрації за гуртову покупку на 15%. Скільки доведеться заплатити за тюльпани?
1) 7200 : 3 = (6000 + 1200) : 3 = 2400 (уп.) – упаковок.
2) 2400 • 28 = 67 200 (грн) – вартість без знижки.
3) 67 200 : 100 • 85 = 57 120 (грн) – вартість після знижки.
Завдання 462
Чи можна двома ударами сокири розрубати підкову на 6 частин, не переміщуючи частин після першого удару? Якщо відповідь ствердна, укажіть, як це зробити.
