Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§19 Прямокутні трикутники, властивості та ознаки рівності прямокутних трикутників
Завдання 494 Малюнок 19.2
1) Зображений трикутник KNM з прямим кутом N називають прямокутним (трикутник, у якого один кут прямий, називають прямокутним).
2) МК – гіпотенуза, KN і NM – катети.
3) Гіпотенуза більша за будь-який катет.
Завдання 495 Малюнок 19.3
1) У прямокутному трикутнику PFL із прямим кутом L маємо РF – гіпотенуза, РL і LF – катети.
2) Яка сторона довша: PL чи PF; LF чи PF?
Гіпотенуза РF більша за катет PL, тому PL < PF.
Гіпотенуза РF більша за катет LF, тому LF < PF.
Завдання 496
На малюнку 19.4 прямокутні трикутники рівні за катетами.
На малюнку 19.5 прямокутні трикутники рівні за катетом і прилеглим кутом.
Завдання 497
1) За якими елементами є рівними прямокутні трикутники на малюнку 19.6. Запишіть відповідні рівності.
Трикутники СМК і ВАР – прямокутні. Гіпотенузи СМ = ВА = 7 см, ∠С = ∠В = 55°. За гіпотенузою і гострим кутом ∆СМК = ∆ВАР.
2) За якими елементами є рівними прямокутні трикутники на малюнках 19.7. Запишіть відповідні рівності.
Гіпотенузи DF = QN, катети EF = LN. За гіпотенузою і катетом ∆DEF = ∆QLN.
Завдання 498
1) Знайдіть гострий кут прямокутного трикутника, якщо інший його гострий кут дорівнює 18°.
Згідно властивості гострих кутів прямокутного трикутника (сума гострих кутів такого трикутника дорівнює 90°) можна записати 90° – 18 ° = 72°.
Відповідь: 72°.
2) Знайдіть гострий кут прямокутного трикутника, якщо інший його гострий кут дорівнює 87°.
Згідно властивості гострих кутів прямокутного трикутника можна записати 90° – 87° = 3°.
Відповідь: 3°.
Завдання 499
1) Знайдіть гострий кут прямокутного трикутника, якщо інший його гострий кут дорівнює 75°.
Згідно властивості гострих кутів прямокутного трикутника можна записати 90° – 75° = 15°.
Відповідь: 15°.
2) Знайдіть гострий кут прямокутного трикутника, якщо інший його гострий кут дорівнює 23°.
Згідно властивості гострих кутів прямокутного трикутника можна записати 90° – 23° = 67°.
Відповідь: 67°.
Завдання 500
Знайдіть кути рівнобедреного прямокутного трикутника.
У прямокутного рівнобедреного трикутника кут при вершині прямий, а прилеглі до основи кути рівні. Застосовуємо теорему про суму кутів трикутника.
1) 180 – 90 = 90 (°) – сума кутів при основі.
2) 90 : 2 = 45 (°) – кут при основі.
Відповідь: 45°, 45°, 90°.
Завдання 501
У рівнобедреному трикутнику один з кутів при основі дорівнює 45°. Чи можна стверджувати, що цей трикутник прямокутний?
У рівнобедреному трикутнику АВС кути при основі рівні, нехай ∠А = ∠В = 45°. Щоб знайти кут С при вершині, застосуємо теорему про суму кутів трикутника, тому ∠С = 180° – (∠А + ∠В) = 180° – (45° + 45°) = 90°. Отже, такий рівнобедрений трикутник є прямокутним.
Завдання 502
1) У прямокутному трикутнику ABC (∠C = 90°) ∠A = 30°. Знайдіть BC, якщо AB = 14 см.
У трикутнику АВС проти кута ∠С = 90° лежить гіпотенуза АВ. Проти кута ∠А = 30° лежить катет ВС, тому ВС = 1/2 АВ = 14 см : 2 = 7 см (катет проти кута 30° дорівнює половині гіпотенузи).
Відповідь: 7 см.
2) У прямокутному трикутнику ABC (∠C = 90°) ∠A = 30°. Знайдіть AB, якщо BC = 5 дм.
У трикутнику АВС проти кута ∠С = 90° лежить гіпотенуза АВ.
Проти кута ∠А = 30° лежить катет ВС, тому ВС = 1/2 АВ.
Звідси АВ = ВС • 2 = 5 дм • 2 = 10 дм
Відповідь: 10 дм.
Завдання 503 Малюнок 19.9
1) У прямокутному трикутнику PFL (∠F = 90°) ∠L = 30°. Знайдіть PF, якщо PL = 12 дм.
У трикутнику PFL проти кута ∠F = 90° лежить гіпотенуза PL. Проти кута ∠L = 30° лежить катет PF, тому PF = 1/2 PL = 12 дм : 2 = 6 дм.
Відповідь: 6 дм.
2) У прямокутному трикутнику PFL (∠F = 90°) ∠L = 30°. Знайдіть PL, якщо PF = 4 см.
У трикутнику PFL проти кута ∠F = 90° лежить гіпотенуза PL. Проти кута ∠L = 30° лежить катет PF, тому PF = 1/2 PL. Звідси PL = PF • 2 = 4 см • 2 = 8 см.
Відповідь: 8 см.
Завдання 504 Малюнок 19.10
BK – висота трикутника ABC. Знайдіть кути трикутника ABC, якщо ∠ABK = 36°, ∠KBC = 64°.
За умовою ВК – висота трикутника АВС, тому ∠ВКА = ∠ВКС = 90°.
За властивістю вимірювання кутів ∠АВС = ∠АВК + ∠КВС = 36° + 64° = 100°.
Трикутник АВК – прямокутний. За властивістю гострих кутів прямокутного трикутника ∠ВАК = 90° – ∠АВК = 90° – 36° = 54°. Точка К належить стороні АС, тому ∠ВАК = ∠ВАС.
Трикутник СКВ – прямокутний. За властивістю гострих кутів прямокутного трикутника ∠ВСК = 90° – ∠КВС = 90° – 64° = 26°. Точка К належить стороні АС, тому ∠ВСК = ∠ВСА.
Відповідь: 26°, 54°, 100°.
Завдання 505 Малюнок 19.11
KLM – рівнобедрений трикутник з основою KM, LN – його медіана. Знайдіть кути трикутника KLM, якщо ∠KLN = 31°.
За умовою, LN – медіана рівнобедреного трикутника є висотою і бісектрисою, тому ∠KNL = ∠MNL = 90° і бісектрисою ∠KLN = ∠MLN, тобто ∠KLM = 2∠KLN = 31° • 2 = 62°.
Для прямокутного трикутника KLN за властивістю гострих кутів можна записати ∠LKN = 90° – ∠KLN = 90° – 31° = 59°. Оскільки точка N належить КМ, тому ∠LKN = ∠LKM. За умовою трикутник рівнобедрений, тому ∠LKM = ∠LMK = 59°.
Відповідь: 59°, 59°, 62°.
Завдання 506 Малюнок 19.12
AB ﬩ AC, KL ﬩ CK, BC = CL. Доведіть, що ∆ABC = ∆KLC.
За умовою AB ﬩ AC і KL ﬩ CK, тому ∠ВАС = 90°, ∠LKC = 90°, трикутники АВС і KLC – прямокутні. Гіпотенузи ВС = CL. Вертикальні кути рівні ∠ВСА = ∠LCK. Отже, за гіпотенузою і гострим кутом прямокутні трикутники ∆ABC = ∆KLC, що треба було довести.
Завдання 507 Малюнок 19.13
MK ﬩ PL, ∠PMK = ∠LMK. Доведіть, що ∆MPK = ∆MLK.
За умовою MK ﬩ PL, тому ∠РКМ = ∠LKM = 90°, трикутники MPK і MLK – прямокутні.
МК – спільний катет трикутників. За умовою прилеглі до цього катета гострі кути ∠PMK = ∠LMK. Отже, за катетом і прилеглим гострим кутом прямокутні трикутники ∆MPK = ∆MLK, що треба було довести.
Завдання 508
1) У трикутнику ABC кут C – прямий. Знайдіть градусні міри кутів A і B, якщо кут A на 28° більший за кут B.
Маємо прямокутний трикутник АВС. Нехай х (°) – градусна міра гострого кута В, х + 28(°) – градусна міра гострого кута А. Складемо рівняння згідно властивості про гострі кути прямокутного трикутника.
х + х + 28 = 90
2х + 28 = 90
2х = 90 – 28
2х = 62
х = 62 : 2
х = 31 (°) – ∠В (О).
х + 28 = 31 + 28 = 59 (°) – ∠А (Т).
Відповідь: ∠В = 31°, ∠А = 59°.
2) У трикутнику ABC кут C – прямий. Знайдіть градусні міри кутів A і B, якщо кут A у 5 разів менший від кута B.
Маємо прямокутний трикутник АВС. Сума гострих кутів прямокутного трикутника дорівнює 90°.
Нехай х (°) – градусна міра кута А, 5х (°) – градусна міра кута В. Складемо рівняння.
х + 5х = 90
6х = 90
х = 90 : 6
х = (60 + 30) : 6
х = 15 (°) – ∠А (К).
5х = 15 • 5 = 75 (°) – ∠В (Н).
Відповідь: ∠А = 15°, ∠В = 75°.
3) У трикутнику ABC кут C – прямий. Знайдіть градусні міри кутів A і B, якщо ∠A : ∠B = 2 : 3.
Маємо прямокутний трикутник АВС.
Нехай х (°) – градусна міра одної частини, тоді 2х (°) – градусна міра кута А, 3х (°) – градусна міра кута В. Складемо рівняння згідно властивості про гострі кути прямокутного трикутника.
2х + 3х = 90
5х = 90
х = 90 : 5
х = (50 + 40) : 5
х = 18 (°) – градусна міра одної частини.
2х = 18 • 2 = 36 (°) – ∠А (Е).
3х = 18 • 3 = 54 (°) – ∠В (С).
Відповідь: ∠А = 36°, ∠В = 54°.
Хто з відомих українців має таке прізвище: українська поетеса Ліна Костенко.
|
15° |
31° |
54° |
59° |
36° |
75° |
15° |
31° |
|
К |
О |
С |
Т |
Е |
Н |
К |
О |
Завдання 509
1) Знайдіть гострі кути прямокутного трикутника, якщо один з них у 4 рази більший за другий.
Нехай х (°) – градусна міра одного гострого кута, 4х (°) – градусна міра іншого гострого кута. Складемо рівняння за властивістю про гострі кути прямокутного трикутника.
х + 4х = 90
5х = 90
х = 90 : 5
х = (50 + 40) : 5
х = 18 (°) – один гострий кут.
4х = 18 • 4 = (10 + 8) • 4 = 72 (°) – другий гострий кут.
Відповідь: 18°, 72°.
2) Знайдіть гострі кути прямокутного трикутника, якщо один з них на 16° менший від другого.
Нехай х (°) – градусна міра меншого гострого кута, тоді х + 16 (°) – градусна міра більшого гострого кута. Складемо рівняння за властивістю про гострі кути прямокутного трикутника.
х + х + 16 = 90
2х + 16 = 90
2х = 90 – 16
2х = 74
х = 74 : 2
х = (60 + 14) : 2
х = 37 (°) – один гострий кут.
х + 16 = 37 + 16 = 53 (°) – другий гострий кут.
Відповідь: 37°, 53°.
3) Знайдіть гострі кути прямокутного трикутника, якщо їхні градусні міри відносяться як 5 : 4.
Нехай х (°) – градусна міра одної частини, тоді 5х (°) – градусна міра одного гострого кута, 4х (°) – градусна міра іншого гострого кута. Складемо рівняння за властивістю про гострі кути прямокутного трикутника.
5х + 4х = 90
9х = 90
х = 90 : 9
х = 10 (°) – градусна міра частини.
5х = 10 • 5 = 50 (°) – один гострий кут.
4х = 10 • 4 = 40 (°) – другий гострий кут.
Відповідь: 40°, 50°.
Завдання 510
Знайдіть менший з кутів, що утворює бісектриса прямого кута трикутника з гіпотенузою, якщо один з гострих кутів трикутника дорівнює 26°.
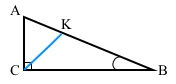
За умовою ∠В = 26°, СК – бісектриса прямого кута С, тоді ∠КСВ = ∠АСВ : 2 = 90° : 2 = 45°. За теоремою про суму кутів трикутника ∠СКВ = 180° – ∠В – ∠КСВ = 180° – 26° – 45° = 109° – більший з кутів перетину. За теоремою про суміжні кути ∠АКС = 180° – ∠СКВ = 180° – 109° = 71° – менший з кутів перетину бісектриси кута з гіпотенузою.
Відповідь: 71°.
Завдання 511
Знайдіть більший з кутів, що утворює бісектриса прямого кута трикутника з гіпотенузою, якщо один з гострих кутів трикутника дорівнює 68°.
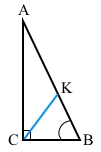
За умовою ∠В = 68°, СК – бісектриса прямого кута С, тоді ∠КСВ = ∠АСВ : 2 = 90° : 2 = 45°. За теоремою про суму кутів трикутника ∠СКВ = 180° – ∠В – ∠КСВ = 180° – 68° – 45° = 67° – менший із кутів перетину. За теоремою про суміжні кути ∠АКС = 180° – ∠СКВ = 180° – 67° = 113° – більший з кутів перетину бісектриси кута з гіпотенузою.
Відповідь: 113°.
Завдання 512
Доведіть, що точка, яка лежить у внутрішній області кута і рівновіддалена від його сторін, належить бісектрисі цього кута.
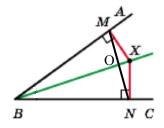
З точки Х опустимо перпендикуляри до сторін кута ХM ﬩ BA, XN ﬩ BC За умовою точка Х рівновіддалена від сторін кута АВС, тому перпендикуляри, опущені з точки до сторін, рівні ХМ = ХN, ∠ВМХ = ∠BNX = 90°.
Проведемо відрізок MN. Трикутник MXN – рівнобедрений, за властивістю рівнобедреного трикутника кути при основі ∠NMX = ∠MNX.
За основною властивістю вимірювання кутів ∠BMX = ∠BMN + ∠NMX, ∠BNX = ∠BNM + ∠MNX, якщо рівні ліві частини, тоді рівні праві ∠BMN = ∠BNM. Трикутник MBN – рівнобедрений за ознакою рівнобедреного трикутника (за двома рівними кутами), тому сторони BM = BN. Прямокутні трикутники ∆BMX = ∆BNX (за двома катетами). У рівних трикутників рівні відповідні кути ∠MBX = ∠NBX, звідси ВХ – бісектриса кута АВС. Отже, точка Х належить бісектрисі, що треба було довести.
Завдання 513
Кут між висотою прямокутного трикутника, проведеною до гіпотенузи, і одним з катетів дорівнює 32°. Знайдіть гострі кути трикутника.
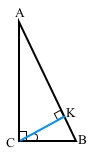
За умовою ∠С = 90°, ∠КСВ = 32°, СК – висота трикутника АВС до гіпотенузи АВ, тоді СК ﬩ АВ. Трикутник СКВ – прямокутний. За властивістю про гострі кути прямокутного трикутника ∠В = 90° – ∠СКВ = 90° – 32° = 58°.
Розглянемо трикутник АВС. За властивістю про гострі кути прямокутного трикутника ∠А = 90° – ∠В = 90° – 58° = 32°.
Відповідь: 32°, 58°.
Завдання 514
Один з кутів, утворених при перетині бісектрис прямого і гострого кутів трикутника, дорівнює 115°. Знайдіть гострі кути цього трикутника.
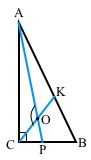
∠АОС = 115°, СК – бісектриса прямого кута С, тоді ∠АСК = ∠С : 2 = 90° : 2 = 45°. Для трикутника САО за теоремою про суму кутів ∠САО = 180° – ∠АСК – ∠АОС = 180° – 45° – 115° = 20°. АР – бісектриса кута А, тоді ∠А = 2∠САО = 20° • 2 = 40°. Для трикутника АВС за властивістю про гострі кути прямокутного трикутника ∠В = 90° – ∠А = 90° – 40° = 50°.
Відповідь: 40°, 50°.
Завдання 515
Доведіть, що два рівнобедрених трикутники рівні, якщо відповідно рівні їхні бічні сторони і висоти, проведені до основ.
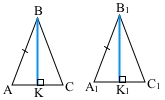
За умовою АВ = А1В1. За означенням рівнобедрених трикутників АВ = ВС, А1В1 = В1С1, оскільки рівні ліві частини, тоді рівні праві частини ВС = В1С1.
ВК – висота трикутника АВС, ВК ﬩ АС. В1К1 – висота трикутника А1В1С1, В1К1 ﬩ А1С1. Розглянемо прямокутні трикутники АКВ і А1К1В1. Гіпотенузи АВ = А1В1, за умовою катети ВК = В1К1, тоді ∆АКВ = ∆А1К1В1 (за катетом і гіпотенузою), отже АК = А1К1.
Трикутники АВС і А1В1С1 – рівнобедрені, тоді АС = 2АК, А1С1 = 2А1К1 (висота є медіаною). Якщо рівні ліві частини, тоді рівні праві частини рівностей, маємо АС = А1С1.
Отже, АВ = А1В1, ВС = В1С1, АС = А1С1, за третьою ознакою рівності трикутників ∆АВС = ∆А1В1С1, що треба було довести.
Завдання 516
У прямокутному трикутнику один з кутів дорівнює 60°, а сума гіпотенузи і меншого катета – 30 см. Знайдіть довжину гіпотенузи та медіани, що проведена до неї.
Проти меншого катета знаходиться менший кут 90° – 60° = 30°. У прямокутному трикутнику катет проти кута 30° дорівнює половині гіпотенузи.
Нехай х (см) – менший катет, тоді 2х (см) – гіпотенуза. Складемо рівняння.
х + 2х = 30
3х = 30
х = 30 : 3
х = 10 (см) – менший катет.
2х = 10 • 2 = 20 (см) – гіпотенуза.
У прямокутному трикутнику медіана, яка проведена до гіпотенузи, дорівнює половині гіпотенузи.
20 : 2 = 10 (см) – медіана, проведена до гіпотенузи.
Відповідь: 20 см, 10 см.
Завдання 517
У прямокутному трикутнику гострий кут дорівнює 60°, а бісектриса цього кута – 4 см. Знайдіть довжину катета, що лежить проти цього кута.
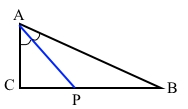
Трикутник АВС – прямокутний, ∠С = 90°, ∠САB = 60°, тоді ∠В = 90° – ∠САВ = 90° – 60° = 30° (за властивістю гострих кутів прямокутного трикутника).
АР – бісектриса кута А, ∠САР = ∠РАВ = ∠САВ : 2 = 60° : 2 = 30°.
Трикутник АВР – рівнобедрений (за ознакою два кути рівні), тому за означенням такого трикутника АР = РВ = 4 см.
У прямокутному трикутнику САР гіпотенуза АР, катет СР лежить проти кута ∠САР = 30°, тому СР = АР : 2 = 4 см : 2 = 2 см.
За властивістю вимірювання відрізків катет СВ = СР + РВ = 2 см + 4 см = 6 см.
Відповідь: 6 см.
Завдання 518
Різниця градусних мір двох зовнішніх кутів при вершинах гострих кутів прямокутного трикутника дорівнює 20°. Знайдіть гострі кути трикутника.
У прямокутному трикутнику один прямий кут і два гострих. Сума суміжних кутів дорівнює 180°.
Нехай х (°) – зовнішній кут при гострому куті, 180 – х (°) – суміжний із ним гострий кут, тоді х + 20 (°) – інший зовнішній кут при гострому куті, 180 – (х + 20) = 160 – х (°) – суміжний з ним гострий кут.
Складемо рівняння за властивістю про гострі кути прямокутного трикутника.
(180 – х) + (160 – х) = 90
180 – х + 160 – х = 90
340 – 2х = 90
340 – 90 = 2х
2х = 250
х = 250 : 2
х = (200 + 40 + 10) : 2
х = 125 (°) – зовнішній кут.
180 – 125 = 55 (°) – суміжний внутрішній гострий кут.
160 – х = 160 – 125 = 35 (°) – інший внутрішній гострий кут.
Відповідь: 35°, 55°.
Завдання 519
Знайдіть градусні міри гострих кутів прямокутного трикутника, якщо градусні міри їхніх зовнішніх кутів відносяться як 2 : 3.
Нехай х (°) – одна частина зовнішніх кутів, 2х (°) – зовнішній кут одного гострого кута трикутника, тоді 180 – 2х (°) – суміжний з ним гострий кут трикутника; а 3х (°) – зовнішній кут іншого гострого кута трикутника, тоді 180 – 3х (°) – суміжний йому гострий кут трикутника.
Складемо рівняння за властивістю гострих кутів прямокутного трикутника.
(180 – 2х) + (180 – 3х) = 90
180 – 2х + 180 – 3х = 90
360 – 5х = 90
360 – 90 = 5х
5х = 270
х = 270 : 5
х = (250 + 20) : 5
х = 54 (°) – частина зовнішнього кута.
180 – 2х = 180 – 54 • 2 = 72 (°) – один гострий кут.
180 – 3х = 180 – 54 • 3 = 18 (°) – другий гострий кут.
Відповідь: 18°, 72°.
Вправи для повторення
Завдання 520
Доведіть, що коли медіана трикутника ділить його на два трикутники з однаковими периметрами, то хоча б два кути трикутника між собою рівні.
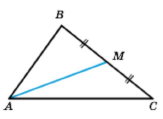
За умовою РВАМ = РСАМ, АМ – медіана до сторони ВС, тоді МВ = МС.
РВАМ = АВ + МВ + АМ, РСАМ = АС + МС + АМ, звідси АВ + МВ + АМ = АС + МС + АМ,
АВ = АС + МС + АМ – АМ – МВ = АС, за означенням трикутник АВС – рівнобедрений. За властивістю рівнобедреного трикутника його кути при основі ∠В = ∠С, що треба було довести.
Завдання 521
Один з кутів трикутника на 20° менший від другого і втричі менший від третього. Знайдіть кожний з кутів трикутника.
Короткий запис
І кут — ?
ІІ кут — на 20°
ІІІ кут — у 3 рази більший
Всього — 180°
Сума кутів трикутника дорівнює 180°.
Нехай х (°) – один кут, тоді х + 20 (°) – другий кут, 3х (°) – третій кут. Складемо рівняння.
х + х + 20 + 3х = 180
5х + 20 = 180
5х = 180 – 20
5х = 160
х = 160 : 5
х = (150 + 10) : 5
х = 32 (°) – один кут.
х + 20 = 32 + 20 = 52 (°) – другий кути.
3х = 32 • 3 = 96 (°) – третій кут.
Відповідь: 32°, 52°, 96°.
Завдання 522
У рівнобедреному трикутнику основа більша за бічну сторону на 3 см, але менша від суми бічних сторін на 4 см. Знайдіть периметр цього трикутника.
Нехай х (см) – бічна сторона, тоді х + х (см) – їхня сума, а х + 3 (см) – основа. Складемо рівняння.
(х + х) – (х + 3) = 4
х + х – х – 3 = 4
х – 3 = 4
х = 4 + 3
х = 7 (см) – бічна сторона рівнобедреного трикутника.
х + 3 = 7 + 3 = 10 (см) – основа у рівнобедреному трикутнику.
Р = 7 • 2 + 10 = 14 + 10 = 24 (см) – периметр.
Відповідь: 24 сантиметри.
Життєва математика
Завдання 523
1 м2 лінолеуму коштує 130 грн. Виміряйте розміри однієї з кімнат (4 х 5 м) та знайдіть площу цієї кімнати. Скільки потрібно заплатити за лінолеум для цієї кімнати?
Короткий запис
а — 5 м
b — 4 м
S — ? м2
1) S = 5 • 4 = 20 (м2) – площа підлоги.
Короткий запис
1 м2 — 130 грн
20 м2 — ? грн
2) 130 • 20 = 2600 (грн) – вартість лінолеуму.
Відповідь: потрібно заплатити 2600 гривень.
Підготуйтеся до вивчення нового матеріалу
Завдання 524
Накресліть довільний ∆АВС, виміряйте довжини трьох його сторін. Порівняйте суму довжин кожної пари сторін із третьою стороною. Зробіть висновки.
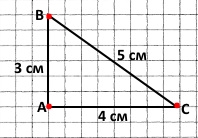
5 см < 3 см + 4 см
3 см < 5 см + 4 см
4 см < 3 см + 5 см
Кожна сторона трикутника менша за суму інших його сторін.
Завдання 525
Позначте вісім точок і сполучіть їх відрізками так, щоб жодні два з них не перетиналися і з кожної точки виходило по чотири відрізки.