ГДЗ геометрія 7 клас Істер коло і круг

Інші завдання дивись тут...

Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."

(умови завдань з підручника подані чорним кольором)

§ 21 Коло і круг

Завдання 610 Малюнок 21.6

Точка O – центр кола.

1) Хорди кола: FK, QC, PL.

2) Діаметр кола: PL.

3) Радіуси кола: OT, OP, OL.

Завдання 611 Малюнок 21.6

Хорду, що проходить через центр кола, називають діаметром (PL).

Завдання 612

1) Обчисліть діаметр кола, якщо його радіус дорівнює 4 см.

d = 2r = 4 см • 2 = 8 см

2) Обчисліть діаметр кола, якщо його радіус дорівнює 3,7 дм.

d = 2r = 3,7 дм • 2 = 7,4 дм

Завдання 613

1) Знайдіть діаметр кола, якщо його радіус дорівнює 7 мм.

d = 2r = 7 мм • 2 = 14 мм

2) Знайдіть діаметр кола, якщо його радіус дорівнює 4,8 см.

d = 2r = 4,8 см • 2 = 9,6 см

Завдання 614

1) Знайдіть радіус кола, якщо його діаметр дорівнює 8 дм.

r = d/2 = 8 дм : 2 = 4 дм

2) Знайдіть радіус кола, якщо його діаметр дорівнює 2,6 см.

r = d/2 = 2,6 см : 2 = 1,3 см

Завдання 615

1) Обчисліть радіус кола, якщо його діаметр дорівнює 18 см.

r = d/2 = 18 см : 2 = 9 см

2) Обчисліть радіус кола, якщо його діаметр дорівнює 3,8 дм.

r = d/2 = 3,8 дм : 2 = 1,9 дм

Завдання 616

Накресліть коло, радіус якого дорівнює 4 см. Проведіть у ньому діаметр MN та хорду MK. Знайдіть ∠NKM.

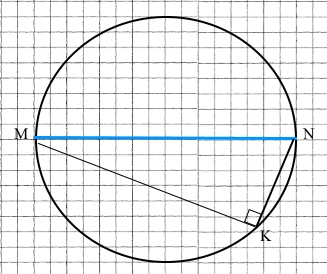
∠NKM = 90°.

Завдання 617

Накресліть коло, радіус якого дорівнює 3,6 см. Проведіть у ньому діаметр AB та хорду BD. Перевірте за допомогою косинця чи транспортира, що ∠BDA – прямий.

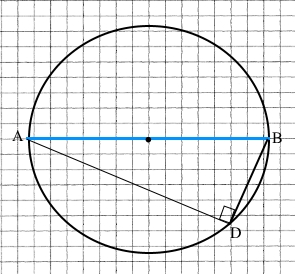
∠BDA = 90°.

Завдання 618

Усередині кола взято довільну точку, відмінну від центра. Скільки діаметрів і скільки хорд можна провести через цю точку?

Можна провести один діаметр, оскільки від має проходити через центр кола, а через дві точки можна провести тільки одну пряму.

Можна провести безліч хорд, оскільки через одну точку можна провести безліч прямих.

Відповідь: 1 діаметр, безліч хорд.

Завдання 619

На колі взято довільну точку. Скільки діаметрів і скільки хорд можна через неї провести?

Можна провести безліч хорд, оскільки через одну точку можна провести безліч прямих.

Відповідь: 1 діаметр, безліч хорд.

Завдання 620

Радіус кола дорівнює 5 см.

d = 2r = 5 см • 2 = 10 см

Хорда має не перевищувати діаметр.

Діаметр – це найбільша хорда.

1) Чи може хорда цього кола дорівнювати 2 см?

Може, оскільки 2 см < 10 см

Відповідь: так.

2) Чи може хорда цього кола дорівнювати 5 см?

Може, оскільки 5 см < 10 см

Відповідь: так.

3) Чи може хорда цього кола дорівнювати 7 см?

Може, оскільки 7 см < 10 см

Відповідь: так.

4) Чи може хорда цього кола дорівнювати 9,8 см?

Може, оскільки 9,8 см < 10 см

Відповідь: так.

5) Чи може хорда цього кола дорівнювати 10,2 см?

Ні, оскільки 10,2 см > 10 см

Відповідь: ні.

6) Чи може хорда цього кола дорівнювати 1 дм?

Може, оскільки 1 дм = 10 см. Хорда буде діаметром.

Відповідь: так.

Завдання 621

Радіус кола дорівнює 4 дм.

d = 2r = 4 дм • 2 = 8 дм

Хорда має не перевищувати діаметр.

Діаметр – це найбільша хорда.

1) Чи може хорда цього кола дорівнювати 1 дм?

Може, оскільки 1 дм < 8 дм

Відповідь: так.

2) Чи може хорда цього кола дорівнювати 4 дм?

Може, оскільки 4 дм < 8 дм

Відповідь: так.

3) Чи може хорда цього кола дорівнювати 6,7 дм?

Може, оскільки 6,7 дм < 8 дм

Відповідь: так.

4) Чи може хорда цього кола дорівнювати 7,95 дм?

Може, оскільки 7,95 дм < 8 дм

Відповідь: так.

5) Чи може хорда цього кола дорівнювати 8,3 дм?

Ні, оскільки 8,3 дм > 8 дм

Відповідь: ні.

6) Чи може хорда цього кола дорівнювати 1 м ?

1 м = 10 дм

Ні, оскільки 10 дм > 8 дм

Відповідь: ні.

Завдання 622 Малюнок 21.7

У колі проведено діаметри AB і CD. Доведіть, що ∆AOD = ∆BOC.

АВ і СD – діаметри, за означенням кола ОА = ОВ = ОС = ОD. Вертикальні кути ∠AOD = ∠BOC (утворені прямими, що перетинаються). Отже, трикутники ∆AOD = ∆BOC за першою ознакою рівності трикутників (сторонами і кутом між ними), що треба було довести.

Завдання 623 Малюнок 21.8

У колі із центром O проведено хорди MN і PK та діаметр PM. ∠POK = ∠MON. Доведіть, що ∆MON = ∆POK.

За означенням кола ОM = ОN = ОK = ОP. За умовою ∠POK = ∠MON. Отже, трикутники ∆POK = ∆MON за першою ознакою рівності трикутників (сторонами і кутом між ними), що треба було довести.

Завдання 624 Малюнок 21.9

1) Точка O – центр кола. Знайдіть градусну міру кута О, якщо ∠A = 52°.

За умовою точка O – центр кола, за означенням кола ОА = ОВ, тому ∆АОВ – рівнобедрений за означенням. За властивістю рівнобедреного трикутника ∠А = ∠В = 52°. За теоремою про суму кутів трикутника ∠О = 180° – (∠А + ∠В) = 180° – (52° + 52°) = 76°.

Відповідь: 76°.

2) Точка O – центр кола. Знайдіть градусну міру кута B, якщо ∠О = 94°.

За умовою точка O – центр кола, за означенням кола ОА = ОВ, тому ∆АОВ – рівнобедрений за означенням. За властивістю рівнобедреного трикутника ∠А = ∠В. За теоремою про суму кутів трикутника ∠В = (180° – ∠О) : 2 = (180° – 94°) : 2 = 43°.

Відповідь: 43°.

Завдання 625 Малюнок 21.9

1) Точка O – центр кола. Знайдіть градусну міру кута О, якщо ∠B = 48°.

За умовою точка O – центр кола, за означенням кола ОА = ОВ, тому ∆АОВ – рівнобедрений за означенням. За властивістю рівнобедреного трикутника ∠А = ∠В = 48°. За теоремою про суму кутів трикутника ∠О = 180° – (∠А + ∠В) = 180° – (48° + 48°) = 84°.

Відповідь: 84°.

2) Точка O – центр кола. Знайдіть градусну міру кута A, якщо ∠О = 102°.

За умовою точка O – центр кола, за означенням кола ОА = ОВ, тому ∆АОВ – рівнобедрений за означенням. За властивістю рівнобедреного трикутника ∠А = ∠В. За теоремою про суму кутів трикутника ∠В = (180° – ∠О) : 2 = (180° – 102°) : 2 = 39°.

Відповідь: 39°.

Завдання 626 Малюнок 21.10

Точка O – центр кола, ∠COA = 32°. Знайдіть ∠CBA.

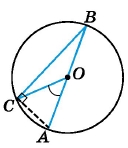
За умовою точка O – центр кола, за означенням кола ОС = ОА. ∆СОА – рівнобедрений за означенням. За властивістю рівнобедреного трикутника ∠ОСА = ∠А.

За теоремою про суму кутів трикутника ∠САО = (180° – ∠СОА) : 2 = (180° – 32°) : 2 = 74°. Оскільки точка В лежить на стороні кута, то ∠САО = ∠САВ.

Проведемо уявно відрізок СА, за теоремою про кут, під яким видно діаметр з точки кола ∠ВСА = 90°. ∆СВА – прямокутний. За властивістю кутів прямокутного трикутника ∠СВА = 90° – ∠САО = 90° – 74° = 16°.

Відповідь: 16°.

Завдання 627 Малюнок 21.10

Точка O – центр кола, ∠BCO = 18°. Знайдіть ∠AOC.

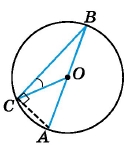
Проведемо уявно відрізок СА, за теоремою про кут, під яким видно діаметр з точки кола ∠ВСА = 90°. За властивістю вимірювання кутів ∠ВСА = ∠ВСО + ∠ОСА, звідси ∠ОСА = ∠ВСА – ∠ВСО = 90° – 18° = 72°.

За умовою точка O – центр кола, за означенням кола ОС = ОВ. ∆СОА – рівнобедрений за означенням. За властивістю рівнобедреного трикутника ∠ОСА = ∠А.

За теоремою про суму кутів трикутника ∠СОА = 180° – 2∠ОСА = 180° – 72° • 2 = 36°

Відповідь: 36°.

Завдання 628

1) Дано коло радіусом 5 см. Проведіть у ньому хорду 6 см завдовжки. Скільки таких хорд можна провести?

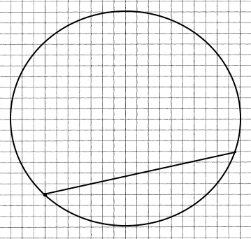
Безліч хорд, бо через точку можна провести безліч прямих.

2) Точка A належить даному колу. Скільки хорд 6 см завдовжки можна провести з даної точки?

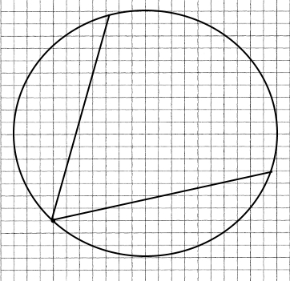
Дві хорди.

Завдання 629 Малюнок 21.11

У колі AB – діаметр, ∠ABM = 60°, BM = 5 см. Знайдіть діаметр кола.

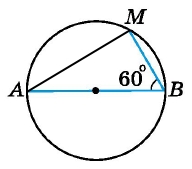
Проведемо відрізок АМ. За теоремою про кут, під яким видно діаметр з точки кола ∠АМВ = 90°, ∆АМВ – прямокутний трикутник. За властивістю кутів прямокутного трикутника ∠ВАМ = 90° – ∠АВМ = 90° – 60° = 30°. Проти кута 30° катет МВ = 1/2 АВ, АВ = 2МВ = 5 см • 2 = 10 см.

Відповідь: 10 см.

Завдання 630 Малюнок 21.11

У колі AB – діаметр, ∠ABM = 60°, AB = 18 см. Знайдіть довжину хорди MB.

Проведемо відрізок АМ. За теоремою про кут, під яким видно діаметр з точки кола ∠АМВ = 90°, ∆АМВ – прямокутний. За властивістю кутів прямокутного трикутника ∠ВАМ = 90° – ∠АВМ = 90° – 60° = 30°. Проти кута 30° катет МВ = 1/2 АВ = 18 см : 2 = 9 см.

Відповідь: 9 см.

Завдання 631 Доведіть, що коли хорди рівновіддалені від центра кола, то вони між собою рівні.

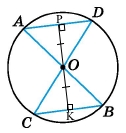
За умовою РК ﬩ AD, PK ﬩ CB, тоді AD || CB. Також перпендикуляри ОР = ОК. Проведемо відрізки DC і AB, DC і АВ – січні для паралельних прямих AD і CB, тоді внутрішні різносторонні кути ∠ADO = ∠BCO, ∠DAO = ∠OBC. Прямокутні трикутники ∆РDO = ∆КСО, ∆РАО = ∆КВО за катетом і протилежним кутом, тоді PD = KC, PA = KB. Точка Р належить AD, точка К належить СВ, тоді за властивістю вимірювання відрізків AD = PA + PD, CB = KC + KB. Оскільки рівні праві частини рівності, тоді рівні ліві AD = CB, що й треба було довести.

Завдання 632 Доведіть, що рівні хорди кола рівновіддалені від його центра.

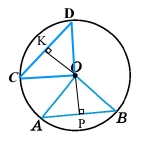
За умовою хорди АВ = CD, О – центр кола, проведемо відрізки OС і ОD, ОА і ОВ. За означенням радіуси кола ОА = ОD = OC = OB. Рівнобедрені трикутники ∆DOС = ∆АOВ (за трьома сторонами), усі кути при основах рівні ∠DCO = ∠CDO = ∠ОАВ = ∠ОВА. Проведемо висоти рівнобедрених трикутників ОК і ОР, ОК ﬩ CD і ОР ﬩ АВ, вони є медіанами СD = 2СК, AB = 2АP, тому СК = АР. Маємо рівні прямокутні трикутники ∆СКО = ∆АРО, тому ОК = ОР, що й треба було довести.

Завдання 633 Хорда кола перетинає його діаметр під кутом 30° і ділиться діаметром на відрізки 4 см і 7 см завдовжки. Знайдіть відстань від кінців хорди до прямої, що містить діаметр кола.

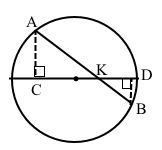
За умовою АС і DB – відстань від кінців хорди, тоді АС ﬩ СD, BD ﬩ CD. За умовою ∠СКА = 30°. У прямокутному ∆САК проти кута 30° катет АС = АК : 2 = 7 : 2 = 3,5 (см).

Вертикальні кути ∠ВКD = ∠CKA = 30°. У прямокутному ∆BDK проти кута 30° катет BD = КB : 2 = 4 : 2 = 2 (см).

Відповідь: 2 см; 3,5 см.

Вправи для повторення

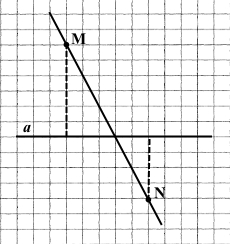
Завдання 634 Побудуйте пряму а, точку M на відстані 3 см від прямої та точку N на відстані 2 см від прямої так, щоб відрізок MN перетинав пряму.

Завдання 635 Два рівних між собою тупих кути мають спільну сторону, а дві інші сторони взаємно перпендикулярні. Знайдіть градусну міру тупого кута.

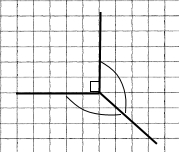
1) 360 – 90 = 270 (°) – сума тупих кутів.

2) 270 : 2 = (200 + 60 + 10) : 2 = 135 (°)

Відповідь: 135°.

Завдання 636 Доведіть рівність двох гострокутних рівнобедрених трикутників за основою і висотою, проведеною до бічної сторони.

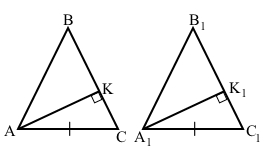
За умовою АВС і А1В1С1 – трикутники рівнобедрені з основами АС і А₁С₁, тоді за властивістю рівнобедрених трикутників ∠А = ∠С, ∠А₁ = ∠С₁.

Також за умовою основи АС = А₁С₁, відрізки АК і А₁К₁ – висоти, тоді АК ﬩ ВС, А₁К₁ ﬩ В₁С₁, причому АК = А₁К₁. Маємо рівні прямокутні трикутники ∆АКС = ∆А₁К₁С₁ (за катетом і гіпотенузою), відповідні кути ∠С = ∠С₁, тоді ∠A = ∠A₁. Отже, трикутники ∆АВС = ∆А₁В₁С₁ (за першою ознакою рівності трикутників), що треба було довести.

Життєва математика

Завдання 637 Скільки потрібно робітників для перенесення дубової балки розміром 6,5 м х 30 см х 45 см? Кожен робітник може підняти в середньому 70 кг. Щільність дуба – 810 кг/м3.

Розв’язання

30 см = (30 : 100) м = 0,3 м

45 см = (45 : 100) м = 0,45 м

1) V = 6,5 • 0,3 • 0,45 = 0,8775 (м3) – об’єм балки.

2) m = ρV = 0,8775 • 810 = 710,775 (кг) – маса балки.

3) 710,775 : 70 = 10,153 (р.) ≈ 11 (р.)

Відповідь: потрібно 11 робітників.

Завдання 638 У коробці шоколадні цукерки квадратної форми викладено у вигляді квадрата в один шар. Марійка з'їла всі цукерки по периметру квадрата – всього 20 цукерок. Скільки цукерок залишилось у коробці?