Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 25 Центральні та вписані кути
Завдання 696
∠3, ∠5 — вписані у коло кути.
Завдання 697
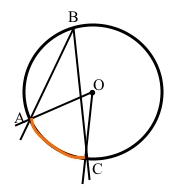
1) Визначте градусну міру кута, вписаного в коло, якщо відповідний йому центральний кут дорівнює 70°.
Градусна міра дуги кола дорівнює градусній мірі центрального кута, який дорівнює 70°.
Дуга, на яку спирається вписаний кут, співпадає з дугою кола центрального кута. Вписаний кут вимірюється половиною дуги, на яку він спирається.
70 : 2 = 35° – градусна міра вписаного кута.
Відповідь: 35°.
2) Визначте градусну міру кута, вписаного в коло, якщо відповідний йому центральний кут дорівнює 190°.
Градусна міра дуги кола дорівнює градусній мірі центрального кута, який дорівнює 190°.
Дуга, на яку спирається вписаний кут, співпадає з дугою кола центрального кута.
Вписаний кут вимірюється половиною дуги, на яку він спирається.
190 : 2 = 95° – градусна міра вписаного кута.
Відповідь: 95°.
Завдання 698

1) Визначте градусну міру центрального кута, якщо градусна міра відповідного йому вписаного кута дорівнює 20°.
Вписаний кут вимірюється половиною дуги, на яку він спирається. Дуга, на яку спирається вписаний кут, співпадає з дугою кола і дорівнює центральному куту.
20° • 2 = 40° – градусна міра центрального кута.
Відповідь: 40°.
2) Визначте градусну міру центрального кута, якщо градусна міра відповідного йому вписаного кута дорівнює 100°.
Вписаний кут вимірюється половиною дуги, на яку він спирається. Дуга, на яку спирається вписаний кут, співпадає з дугою кола і дорівнює центральному куту.
100° • 2 = 200° – градусна міра центрального кута.
Відповідь: 200°.
Завдання 699
Точки A і B належать колу й лежать по один бік від хорди CD. Знайдіть ∠CAD, якщо ∠CBD = 55°.
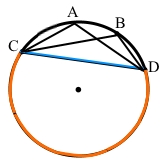
Вписаний кут ∠CВD = 55° спирається на ͜ CD,
вписаний кут ∠CAD також спирається на ͜ CD.
За наслідком з теореми про вписаний кут ∠CAD = ∠CBD = 55°.
Відповідь: 55°.
Завдання 700
Точки A і B належать колу й лежать по різні боки від хорди MN. Доведіть, що ∠MAN + ∠MBN = 180°.
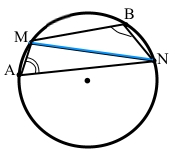
Вписаний кут MAN спирається на дугу MBN, тому ∠MAN = ½ ͜ MBN (за теоремою про вписаний кут).
Вписаний кут MBN спирається на дугу MAN, тому ∠MBN = ½ ͜ MAN (за теоремою про вписаний кут).
∠MAN + ∠MBN = ½ ͜ MBN + ½ ͜ MAN = ½ ( ͜ MBN + ͜ MBN) = ½ • 360° = 180°, отже ∠MAN + ∠MBN = 180°, що треба було довести.
Завдання 701
Точки M і N належать колу й лежать по різні боки від хорди AB. Знайдіть ∠AMB, якщо ∠ANB = 70°.
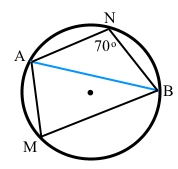
Вписаний кут ∠ANB = 70° спирається на дугу ͜ AMB. За теоремою про вписаний кут ∠ANB = ½ ͜ AMB, звідси ͜ AMB = 2∠ANB = 2 • 70° = 140°.
͜ ANB = 360° – ͜ AMB = 360° – 140° = 220°.
Вписаний кут ∠AMB спирається на ͜ ANB. За теоремою про вписаний кут ∠AMB = ½ ͜ ANB = 220° : 2 = 110°.
Відповідь: ∠AМB = 110°.
Завдання 702
Точка P кола і його центр O лежать по різні боки від хорди CD. Знайдіть ∠COD, якщо ∠CPD = 126°.
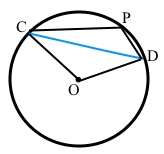
∠COD – центральний кут, який утворює дугу кола ͜ CРD, ∠CРD = 126° – вписаний, який спирається на дугу ͜ CD.
За теоремою про вписаний кут ∠СPD = ½ ͜ СD, звідси ͜ CD = 2∠CPD = 2 • 126° = 252°.
͜ CPD = 360° – ͜ CD = 360° – 252° = 108°.
Дуга кола дорівнює градусній мірі відповідного центрального кута, тому ∠COD = ͜ CPD = 108°.
Відповідь: ∠COD = 108°.
Завдання 703
Точка A кола і його центр O лежать по різні боки від хорди LK. Знайдіть ∠LAK, якщо ∠LOK = 128°.
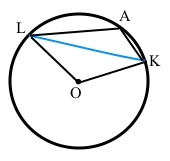
∠LOK = 128° – центральний кут, який утворює дугу кола ͜ LАK, ∠LAK – вписаний, який спирається на дугу ͜ LK.
Дуга кола дорівнює градусній мірі відповідного центрального кута, тому ͜ LАК = ∠LOK = 128°.
͜ LK = 360° – ͜ LAK = 360° – 128° = 232°.
За теоремою про вписаний кут ∠LAK = ½ ͜ LK = 232° : 2 = 116°.
Відповідь: ∠LAK = 116°.
Завдання 704
Хорда розбиває коло на дві дуги у відношенні 1 : 2. Знайдіть міри вписаних кутів, що спираються на ці дуги.
Сума двох дуг, на які коло розбивається хордою, дорівнює 360°.
Нехай х (°) – градусна міра першої дуги, тоді 2х (°) – градусна міра другої дуги.
Складемо рівняння.
х + 2х = 360
3х = 360
х = 360 : 3
х = 120 (°) – перша дуга.
2х = 120 • 2 = 240 (°) – друга дуга.
За теоремою про вписаний кут він дорівнює половині градусної міри дуги, на яку він спирається.
120 : 2 = 60 (°) – перший вписаний кут.
240 : 2 = 120 (°) – другий вписаний кут.
Відповідь: 60°, 120°.
Завдання 705
Хорда AB дорівнює радіусу кола. Точка C кола і його центр лежать по один бік від хорди AB. Знайдіть ∠ACB.
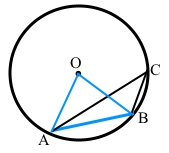
За умовою хорда АВ = ОА = ОВ, де ОА і ОВ – радіуси кола. Трикутник АОВ – рівносторонній (за означенням), ∠АОВ = 60°.
∠АОВ – центральний кут, його дуга кола ͜ АВ = ∠АОВ = 60°.
Вписаний кут ∠АСВ також спирається на дугу ͜ АВ.
За теоремою про вписаний кут ∠АСВ = ½ ͜ АВ = 60° : 2 = 30°.
Відповідь: ∠АСВ = 30°.
Завдання 706
Хорди AD і BC перетинаються в точці F. ∠ABC = 20°, ∠BCD = 80°. Знайдіть градусну міру кута AFB.
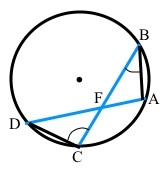
Вписаний кут ∠BCD = 80° спирається на дугу ͜ BD, вписаний кут ∠DAB також спирається на дугу ͜ BD, тому ∠DAB = ∠BCD = 80° (за наслідком з теореми про вписаний кут). Точка F належить хорді АD, тоді ∠FAB = ∠DAB = 80°.
Точка F належить хорді ВС, тоді ∠АВF = ∠ABC = 20°.
За теоремою про суму кутів трикутника AFB знайдемо ∠AFB = 180° – (∠FAB + ∠ABF) = 180° – (80° + 20°) = 80°.
Відповідь: ∠AFB = 80°.
Завдання 707
Хорди AB і CD перетинаються в точці M. ∠ABC = 35°, ∠BAD = 55°. Доведіть, що хорди AB і CD взаємно перпендикулярні.
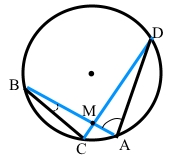
Вписаний кут ∠ABC = 35° спирається на дугу ͜ CA, вписаний кут ∠CDA також спирається на дугу ͜ CA, тому ∠CDA = ∠ABC = 35° (за наслідком з теореми про вписаний кут). Точка M належить хорді CD, тоді ∠MDA = ∠CDA = 35°.
Точка M належить хорді AB, тоді ∠MAD = ∠BAD = 55°.
За теоремою про суму кутів трикутника AMD знайдемо ∠AMD = 180° – (∠MDA + ∠MAD) = 180° – (35° + 55°) = 90°. Хорди AB і CD перетинаються під прямим кутом (∠AMD = 90°), отже за означенням АВ ﬩ CD, що треба було довести.
Завдання 708
O – центр кола, ∠MBA = 50°. Знайдіть x.
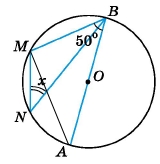
Проведемо відрізок МА. Вписаний кут, який спирається на діаметр прямий, тому ∠АМВ = 90° (наслідок з теореми про вписаний кут).
∆АМВ – прямокутний, за теоремою про суму його гострих кутів ∠МАВ = 90° – ∠МВА = 90° – 50° = 40°.
Вписаний кут ∠МАВ = 40° спирається на дугу ͜ МВ, вписаний кут ∠MNB також спирається на дугу ͜ MB, тому x = ∠MNB = ∠MAB = 40° (за наслідком з теореми про вписаний кут).
Відповідь: х = 40°.
Завдання 709
Доведіть, що кут між дотичною і хордою, що виходить з точки дотику, дорівнює половині дуги, яка лежить між сторонами кута, тобто ∠CAB = ½ ͜ CNA.
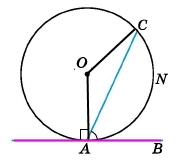
За умовою АВ – дотична до кола (ОА ﬩ АВ), ∠ОАВ = 90°.
Центральний кут АОС утворює дугу кола СAN, тому ∠АОС = ͜ CAN (за означенням дуги кола).
Відрізки ОА = ОС – радіуси кола з центром у точці О, звідси ∆АОС – рівнобедрений з основою АС (за означенням), за властивістю кутів рівнобедреного трикутника ∠ОАС = ∠ОСА.
За теоремою про суму кутів трикутника ∠АОС + ∠ОАС + ∠ОСА = ∠АОС + 2∠ОАС = 180°, ∠ОАС = (180° – ∠АОС) : 2 = 90° – ½ ∠АОС.
За властивістю вимірювання кутів ∠ОАВ = ∠ОАС + 90, звідси ∠САВ = 90° – ∠ОАС = 90 – (90 – ½ ∠АОС) = 90° – 90° + ½ ∠АОС, отже, ∠САВ = ½ ͜ CAN, що треба було довести.
Завдання 710
Рівнобедрений трикутник ABC вписано в коло із центром у точці O, ∠AOB = 80°. Знайдіть кути трикутника ABC. Скільки розв'язків має задача?
Рівнобедрений трикутник ABC вписано в коло із центром у точці O, тоді коло з центром О описане навколо цього трикутника.
Задача має три розв’язки.
І варіант
Центр кола О всередині трикутника АВС. Дуга кола центрального кута АОВ є дугою, на який спирається вписаний кут, проведений із вершини рівнобедреного трикутника.
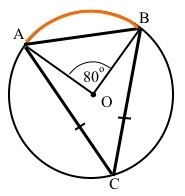
Центральний кут АОВ утворює дугу кола ͜ АВ, ͜ АВ = ∠АОВ = 80°.
Кут трикутника ∠С = ∠АСВ – є вписаним кутом, який спирається на дугу ͜ АВ, за теоремою про вписаний кут ∠АСВ = ½ ͜ АВ = 80° : 2 = 40°.
Кут при вершині рівнобедреного трикутника ∠С = 40°.
За умовою ∆АВС – рівнобедрений з основою АВ, тоді за властивістю кутів такого трикутника ∠А = ∠В.
За теоремою про суму кутів трикутника ∠С + ∠А + ∠В = ∠С + 2∠В = 180°, звідки ∠А = ∠В = (180° – ∠С) : 2 = (180° – 40°) : 2 = 70°.
Відповідь: 40°, 70°, 70°.
ІІ варіант
Центр кола О поза трикутником АВС. Жодний кут трикутника не є вписаним кутом, який спирається на дугу, яка є дугою кола центрального кута АОВ.
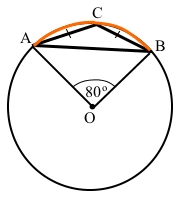
За умовою ∠АОВ = 80° – центральний кут утворює дугу кола ͜ АСВ = ∠АОВ = 80°.
Кут трикутника ∠АСВ – є вписаним кутом, який спирається на дугу ͜ АВ.
Дуга ͜ АВ = 360° – ͜ АСВ = 360° – 80° = 280°.
За теоремою про вписаний кут ∠АСВ = ½ ͜ АВ = 280° : 2 = 140°.
Кут при вершині рівнобедреного трикутника ∠АСВ = 140°.
За умовою ∆АВС – рівнобедрений з основою АВ, за властивістю кутів такого трикутника ∠САВ = ∠СВА.
За теоремою про суму кутів трикутника ∠АСВ + ∠САВ + ∠СВА = ∠АСВ + 2∠САВ = 180°, звідки ∠САВ = ∠СВА = (180° – ∠АСВ) : 2 = (180° – 140°) : 2 = 20°.
Відповідь: 140°, 20°, 20°.
ІІІ варіант
Центр кола О поза трикутником АВС. Дуга кола центрального кута АОВ є дугою, на який спирається вписаний кут, проведений не із вершини рівнобедреного трикутника.
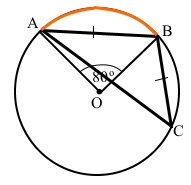
Центральний кут АОВ утворює дугу кола ͜ АВ, ͜ АВ = ∠АОВ = 80°.
Кут трикутника ∠BCA – є вписаним кутом, який спирається на дугу ͜ АВ, за теоремою про вписаний кут ∠BCA = ½ ͜ АВ = 80° : 2 = 40°.
За умовою ∆АВС – рівнобедрений з основою АС, тоді за властивістю кутів такого трикутника ∠BCA = ∠BAC.
Кути трикутника при основі ∠BCA = ∠BAC = 40°.
За теоремою про суму кутів трикутника ∠ABC + ∠BCA + ∠BAC = ∠ABC + 2∠BCA = 180°, звідки ∠ABC = 180° – 2∠BCA = 180° – 40° • 2 = 100°.
Відповідь: 100°, 40°, 40°.
Завдання 711
Рівнобедрений трикутник MNK вписано в коло із центром у точці O, ∠MOK = 100°. Знайдіть кути трикутника MNK. Скільки розв'язків має задача?
Рівнобедрений трикутник ABC вписано в коло із центром у точці O, тоді коло з центром О описане навколо цього трикутника.
Задача має три розв’язки.
І варіант
Центр кола О всередині трикутника MNK. Дуга кола центрального кута MOK є дугою, на який спирається вписаний кут, проведений із вершини рівнобедреного трикутника.
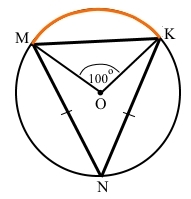
За умовою центральний кут MOK утворює дугу кола ͜ MK, ͜ MK = ∠MOK = 100°.
Кут трикутника ∠N = ∠MNK – є вписаним кутом, який спирається на дугу ͜ MK, за теоремою про вписаний кут ∠MNK = ½ ͜ MK = 100° : 2 = 50°.
Кут при вершині рівнобедреного трикутника ∠N = 50°.
За умовою ∆MNK – рівнобедрений з основою MK, тоді за властивістю кутів такого трикутника ∠M = ∠K.
За теоремою про суму кутів трикутника ∠N + ∠M + ∠K = ∠N + 2∠M = 180°, звідки ∠M = ∠K = (180° – ∠N) : 2 = (180° – 50°) : 2 = 65°.
Відповідь: 50°, 65°, 65°.
ІІ варіант
Центр кола О поза трикутником MNK. Жодний кут трикутника не є вписаним кутом, який спирається на дугу, яка є дугою кола центрального кута MOK.
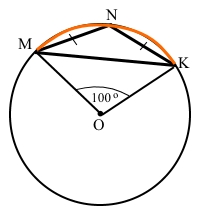
За умовою ∠MOK = 100° – центральний кут утворює дугу кола ͜ MNK = ∠MOK = 100°.
Кут трикутника ∠MNK – є вписаним кутом, який спирається на дугу ͜ MK.
Дуга ͜ MK = 360° – ͜ MNK = 360° – 100° = 260°.
За теоремою про вписаний кут ∠MNK = ½ ͜ MK = 260° : 2 = 130°.
Кут при вершині рівнобедреного трикутника ∠MNK = 130°.
За умовою ∆MNK – рівнобедрений з основою MK, за властивістю кутів такого трикутника ∠NMK = ∠NKM.
За теоремою про суму кутів трикутника ∠MNK + ∠NMK + ∠NKM = ∠MNK + 2∠NMK = 180°, звідки ∠NMK = ∠NKM = (180° – ∠MNK) : 2 = (180° – 130°) : 2 = 25°.
Відповідь: 130°, 25°, 25°.
ІІІ варіант
Центр кола О всередині трикутника MNK. Дуга кола центрального кута MOK є дугою, на який спирається вписаний кут, проведений не із вершини рівнобедреного трикутника.

Центральний кут MOK утворює дугу кола ͜ MK, ͜ MK = ∠MOK = 100°.
Кут трикутника ∠MNK – є вписаним кутом, який спирається на дугу ͜ MK, за теоремою про вписаний кут ∠MNK = ½ ͜ MK = 100° : 2 = 50°.
За умовою ∆MNK – рівнобедрений з основою MN, тоді за властивістю кутів такого трикутника ∠KMN = ∠KNM.
Кути трикутника при основі ∠KMN = ∠KNM = 50°.
За теоремою про суму кутів трикутника ∠MKN + ∠KMN + ∠KNM = ∠MKN + 2∠KNM = 180°, звідки ∠MKN = 180° – 2∠KMN = 180° – 50° • 2 = 80°.
Відповідь: 80°, 50°, 50°.
Завдання 712
Коло поділено трьома точками на частини, які відносяться як 1 : 2 : 6, і точки поділу сполучено між собою. Знайдіть кути утвореного трикутника.
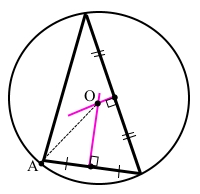
Кути утвореного трикутника є вписаними кутами, які спираються на три дуги, що сумарно дають градусну міру дуги, яка є колом.
Градусна міра дуги, що є колом дорівнює 360°.
Нехай х (°) – градусна міра першої дуги, тоді 2х (°) – градусна міра другої дуги, 6х (°) – градусна міра третьої дуги.
Складемо рівняння.
х + 2х + 6х = 360
9х = 360
х = 360 : 9
х = 40 (°) – перша дуга.
2х = 40 • 2 = 80 (°) – друга дуга.
6х = 40 • 6 = 240 (°) – третя дуга.
За теоремою про вписаний кут він дорівнює половині градусної міри дуги, на яку він спирається.
40 : 2 = 20 (°) – перший вписаний кут.
80 : 2 = 40 (°) – другий вписаний кут.
240 : 2 = 120 (°) – другий вписаний кут.
Відповідь: 20°, 40°, 120°.
Для повторення
Завдання 713
Дано кут 30°. Коло радіусом 5 см дотикається до сторони кута і має центр на його іншій стороні. Обчисліть відстань від центра кола до вершини кута.
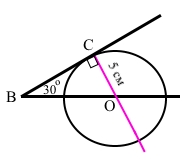
За умовою ∠СВО = 30°, радіус кола СО = 5 см дотикається до сторони ВС, тоді ОС ﬩ ВС. ∆ВСО – прямокутний трикутник (∠ВСО = 90°). Катет СО = ½ ВО (катет проти кута 30° дорівнює половині гіпотенузи), звідки ВО = 2СО = 5 см • 2 = 10 см.
Відповідь: 10 см.
Завдання 714
Випишіть у порядку зростання внутрішні кути трикутника ABC, якщо AB = 5 см, BC = 9 см, AC = 6 см.
Більша сторона трикутника лежить проти більшого кута.
Сторона АВ = 5 см лежить проти кута ∠С.
Сторона АС = 6 см лежить проти кута ∠В.
Сторона ВС = 9 см лежить проти кута ∠А.
Внутрішні кути трикутника у порядку зростання (від меншого до більшого):
∠С, ∠В, ∠А.
Життєва математика
Завдання 715
Щоб витягти з колодязя відро води, потрібно зробити 12 обертів вала. Знайдіть глибину колодязя, якщо діаметр вала дорівнює 32 см. Для спрощення обчислень вважайте, що π ≈ 3.
Розв’язання
1) l = πd = 32 • 3 = 96 (см) – довжина вала.
2) 96 • 12 = 1152 (см) = 11 км 52 см – глибина колодязя.
Відповідь: глибина колодязя 11 км 52 м.
Підготуйтеся до вивчення нового матеріалу
Завдання 716
1) Накресліть відрізок MN завдовжки 6 см. Узявши точки М і N за центри, проведіть два кола, одне з яких (із центром у точці М) радіусом 4 см, а друге (із центром у точці N) радіусом 2 см.
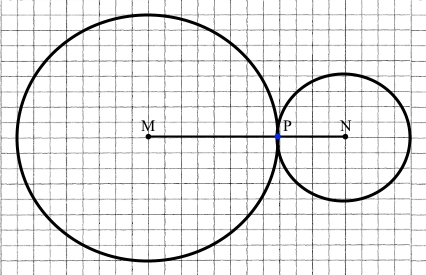
2) Ці кола мають одну спільну точку Р.
MN = 6 см, МР = 4 см, NР = 2 см, МР + NР = MN, точка Р є MN.
Завдання 717
1) Накресліть відрізок AB завдовжки 5 см. Узявши точки A і B за центри, проведіть два кола, одне з яких (із центром у точці A) радіусом 3 см, а друге (із центром у точці B) радіусом 4 см.
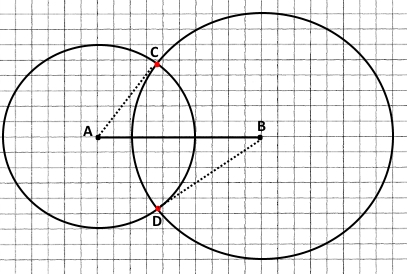
2) Ці два кола мають дві спільні точки.
АВ = 5 см, АС = 3 см, ВС = 4 см, виконується нерівність трикутника для найбільшої сторони (5 см < 3 см + 4 см), точки А, В, С не можуть лежати на одній прямій.
Відповідно АВ = 5 см, АD = 3 см, ВD = 4 см, виконується нерівність трикутника для найбільшої сторони (5 см < 3 см + 4 см), точки А, В, D не можуть лежати на одній прямій.
Цікаві задачі
Завдання 718
У кожній клітинці прямокутної дошки (шахової) розміром 2025 х 2027 клітинок сидить жук. За сигналом усі жуки переповзають на сусідні (по горизонталі або вертикалі) клітинки. Чи обов'язково при цьому залишиться вільна клітинка?
Добуток чисел – непарне число (у розряді одиниць 5, бо 5 • 7 = 35), тому кількість чорних і білих клітинок різна, відповідно кількість жуків, що сидять на них також різна.
За сигналом усі жуки переповзають на сусідні (по горизонталі або вертикалі) клітинки. Маємо умову переміщення жуків: жук із чорної клітинки може попасти тільки в білу, а з білої клітинки – тільки у чорну.
Нехай білих клітинок більше, ніж чорних, відповідно жуків на білих клітинках більше, ніж жуків на чорних клітинках.
У такому випадку тепер жуки, які спочатку були на чорних клітинках, не зможуть зайняти всі білі клітинки. Якщо чорних клітинок більше, після переміщення залишаться вільні чорні клітинки, і навпаки.
Отже, після переміщення жуків обов’язково залишиться вільна клітинка.