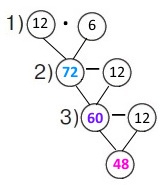
© Барна Р., 2021
Серія "Вчимось разом" до робочого зошита "Математика 4 клас Лишенко Г."
Сторінка 63
Завдання 5 Складена задача на множення
Три муляри за 4 год уклали 3360 цеглин, порівну кожний. Скільки цеглин уклав один муляр за З год?
|
Цеглин 1 муляр за 1 год |
Кількість годин (час роботи) |
Кількість мулярів |
Загальна кількість цеглин (виробіток) |
|
? |
4 |
3 |
3360 |
|
однаково |
3 год |
|
? |
Розв'язання
3360 : 4 = (3200 + 160) : 4 = 840 (ц.) – цеглин уклали 3 мулярі за 1 год.
840 : 3 = (600 + 240) : 3 = 280 (ц.) – цеглин уклав 1 муляр за 1 год.
280 • 3 = (200 + 80) • 3 = 840 (ц.) – цеглин уклав 1 муляр за 3 год.
2 спосіб
3360 : 3 = (3000 + 300 + 60) : 3 = 1120 (ц.) – цеглин уклав 1 муляр за 3 год.
1120 : 4 = (1200 – 80) : 4 = 280 (ц.) – цеглин уклав 1 муляр за 1 год.
280 • 3 = 840 (ц.) – цеглин уклав 1 муляр за 3 год.
3 спосіб
3 • 4 = 12 (год) – годин працювали мулярі.
3360 : 12 = 280 (ц.) – цеглин укладає 1 муляр за 1 год.
280 • 3 = 840 (ц.) – цеглин уклав 1 муляр за 3 год.
Відповідь: за три години муляр уклав 840 цеглин.
До №305 – 326
Завдання 1 Дії з величинами
6 м 35 см • 8 = 50 м 80 см 7 кг 90 г • 7 = 49 кг 630 г
23 м 4 см • 3 = 69 м 12 см 35 ц 8 кг • 4 = 14 т 32 кг
42 м 10 см • 2 = 84 м 20 см 81 ц 2 кг • 3 = 24 т 3 ц 6 кг
|
х6 м 35 см 8 50 м 80 см |
х42 м 10 см 2 84 м 20 см |
х35 ц 08 кг 4 140 ц 32 кг |
|
х23 м 04 см 3 69 м 12 см |
х7 кг 090 г 7 49 кг 630 г |
х81 ц 02 кг 3 243 ц 06 кг |
Завдання 2 Письмове ділення
|
_35147 | 7 35 5021 _14 14 _7 7 0 |
х5021 7 35147 |
_28032| 4 28 7008 _32 32 0 |
х7008 4 28032 |
Сторінка 64
Завдання 3
Площа прямокутника 1600 м2, а довжина сторони 80 м. Знайди площу квадрата, периметр якого дорівнює периметру прямокутника.
Розв'язання
1) 1600 : 80 = 20 (м) – ширина прямокутника.
2) Р = (80 + 20) • 2 = 200 (м) – периметр прямокутника.
3) 200 : 4 = 50 (м) – сторона квадрата.
4) 50 • 50 = 2500 (м2) – площа квадрата.
Відповідь: площа квадрата дорівнює 2500 м2.
Завдання 4 Проста задача на зменшення на деяке число в непрямій формі
Висота найвищої вершини Карпат Говерли 2061 м. Це на 516 м вище (більше метрів) від вершини Роман-Кош, що в Криму. Яка заввишки Роман-Кош?
Короткий запис
Говерла — 2061 м, це на 516 м більше
Роман-Кош — ?
Розв'язання
2061 – 516 = 1561 – 11 – 5 = 1545 (м) – висота Роман-Кош.
Відповідь: Роман-Кош заввишки 1545 метри.
Завдання 5 Складена задача на різницеве порівняння
Турист мав пройти 36 км. Після привалу йому залишилося пройти ще третину того, що пройшов до привалу. На скільки кілометрів менше залишилося пройти туристу, ніж він уже пройшов?
Розв'язання
До привалу турист пройшов 3 частини шляху, після привалу одну 1 частину шляху, тому увесь шлях складається із 4 частин.
1) 36 : 4 • 3 = 27 (км) – пройшов турист до привалу.
2) 36 : 4 • 1 = 9 (км) – пройшов турист після привалу.
3) 27 – 9 = 18 (км) – на стільки кілометрів менше залишилося пройти туристу, ніж він уже пройшов.
2 спосіб
До привалу турист пройшов 3 частини шляху, після привалу одну 1 частину шляху, тому увесь шлях складається з 4 частин.
3 – 1 = 2 (частини) – на стільки частин шлях після привалу менший.
36 : 4 • 2 = 18 (км) – на стільки кілометрів шлях після привалу менший.
Відповідь: на 18 кілометрів менше залишилося пройти.
До № 327 – 348
Завдання 1 Порядок дій
|
60 • 40 : 24 • 90 : 5 1800 |
180 : 3 • 70 : 6 • 0 0 |
1400 : 7 • 20 : 5 • 6 4800 |
50 000 : 5 : 2 • 8 : 100 400 |
|
60 • 40 = 24 • 10 • 10 = 24 • 100 = 2400 2400 : 24 = 24 сот. : 24 = 1 сот. = 100 100 • 90 = 9 • 1000 = 9000 9000 : 5 = 9000 : 10 • 2 = 900 • 2 = 1800 |
1400 : 7 = 14 • 100 : 7 = 14 : 7 • 100 = 200 200 • 20 = 4 • 1000 = 4000 4000 : 5 = 800 800 • 6 = 48 • 100 = 4800 |
||
|
180 : 3 = 18 дес. : 3 = 6 дес. = 60 60 • 70 = 6 • 7 • 10 • 10 = 42 • 100 = 4200 4200 : 6 = 42 сот. : 6 = 7 сот. = 700 700 • 0 = 0 |
50 000 : 5 = 5 : 5 • 10000 = 10000 10000 : 2 = 10 : 2 • 1000 = 5000 5000 • 8 = 40 • 1000 = 40000 40000 : 100 = 400 |
||
Сторінка 65
Завдання 2 Одиниці вимірювання
|
23 м 40 см : 3 = 2340 см : 3 = 780 см = 7 м 80 см 54 км 36 м : 9 = 54036 м : 9 = 6004 м = 6 км 4 м |
35 ц 80 кг : 4 = 3580 кг : 4 = 895 кг = 8 ц 95 кг 2 т 40 кг : 5 = 2040 кг : 5 = 408 кг |
||
|
_2340 | 3 21 780 _24 24 0 |
_54036 | 9 54 6004 _36 36 0 |
_3580 | 4 32 895 _38 36 _40 40 0 |
_2040 | 5 20 48 _40 40 0 |
Завдання 3 Складена задача на кратне порівняння
За 2 год бульдозер розчищає 12 га (12 000 м2) землі, а робітник за 6 год — 180 м2 . Скількох робітників замінює один бульдозер?
|
|
Площа за 1 год (м2) (продуктивність праці) |
Кількість год (час роботи) |
Загальна площа (м2) (виробіток) |
|
Бульдозер |
?, у ? разів більше |
2 |
12000 |
|
Робітник |
? |
6 |
180 |
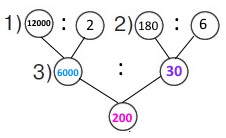
Розв'язання
12 га = 1 га • 12 = 1000 м2 • 12 = 12 000 м2
1) 12000 : 2 = 6000 (м2) – площу розчищає бульдозер за 1 год.
2) 180 : 6 = 30 (м2) – площу розчищає робітник за 1 год.
Щоб дізнатися, скільки робітників замінює бульдозер, треба знайти у скільки разів більше площі обробить бульдозер, ніж робітник, тому
3) 6000 : 30 = 200 (р.) – робітників заміняє один бульдозер.
Відповідь: бульдозер заміняє 200 робітників.
Завдання 4 Проста задача на знаходження від’ємника
24 серпня 1991 року в день проголошення незалежності України народився хлопчик Ярослав. Визнач вік Ярослава на сьогодні.
Короткий запис
Було — 1991 рік
Пройшло (вік) — ?
Стало — 2023 рік
Розв'язання
2023 – 1991 = 2023 – 2000 + 9 = 23 + 7 + 2 = 32 (р.) – років Ярославу.
Відповідь: Ярославу 32 роки.
Завдання 5
Сума чисел, що позначають номери трьох будинків, які стоять поряд на одному боці вулиці, дорівнює 147. Визнач номери цих будинків.
147 : 3 = 49 (н.) – номер середнього будинку.
Якщо середній номер непарний, то будинки знаходяться на стороні непарних номерів, тому маємо 47, 49, 51.
Відповідь: номери цих будинків 47, 49, 51.
Сторінка 66 До №349 – 369
Завдання 1
42 000 : 7 = 42 тис. : 7 = 6 тис. = 6 000
36 т 42 кг : 6 = (36 т + 42 кг) : 6 = 6 т + 7 кг = 6 т 7 кг
2 т 40 кг : 8 = 2040 кг : 8 = (1600 кг + 400 кг + 40 кг) : 8 = 200 кг + 50 кг + 5 кг = 255 кг
16 000 : 4 = 16 тис. : 4 = 4 тис. = 4 000
48 км 180 м : 3 = 48 180 м : 3 = (30 000 м + 18 000 м + 180 м) : 3 = 10 000 м + 6 000 м + 60 м = 16 060 м = 16 км 60 м
3 км 500 м : 7 = 3 500 м : 7 = 500 м
Завдання 2
З двох міст одночасно назустріч один одному виїхали автобус і легковий автомобіль. Швидкість автобуса 60 км/год, а легкового автомобіля — 80 км/год. Через 3 год вони зустрілися. Яка відстань між містами?
|
Vавтобус = 60 км/год t = 3 год Vавтомобіль = 80 км/год ------------------------------>∆<-------------------------------------------- S — ? км |
Розв’язання
1 спосіб
План розв’язування
1) Яку відстань проїхав автобус? 60 • 3 = 180 (км)
2) Яку відстань проїхав автомобіль? 80 • 3 = 240 (км)
3) Яка відстань між містами? 180 + 240 = 420 (км)
60 • 3 + 80 • 3 = 420 (км)
|
2 спосіб План розв’язування 1) Яка швидкість зближення? 60 + 80 = 140 (км/год) 2) Яка відстань? 140 • 3 = 420 (км) (60 + 80) • 3 = 420 (км) |
3 спосіб План розв’язування 1) Яку відстань проїдуть разом за 1 год? 60 + 80 = 140 (км) 2) Яку відстань проїдуть за 3 год? 140 • 3 = 420 (км) (60 + 80) • 3 = 240 (км) |
Відповідь: відстань між містами 240 кілометрів.
Завдання З Рівняння
|
8 • х = 72 045 х = 72 045 : 8 х = 8005 |
240000 : х = 8 х = 240 000 : 8 х = 30 000 |
Завдання 4 Складена задача на множення
На 1 м2 картопляного поля вносять 3 кг перегною. Скільки кілограмів перегною потрібно внести на ділянку прямокутної форми, довжина якої 70 м, а ширина — 8 м?
|
Маса на 1 м2 |
Площа ділянки |
Маса на площу ділянки |
|
3 кг |
? |
? |
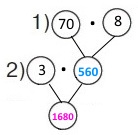
Вираз 3 • (70 • 8)
Розв'язання
1) 70 • 8 = 560 (м2) – площа прямокутної ділянки.
2) 3 • 560 = 3 • (500 + 60) = 1500 + 180 = 1680 (кг) – кілограмів перегною потрібно внести.
Відповідь: потрібно внести 1680 кілограмів перегною.
Сторінка 67
Завдання 5
Периметр прямокутника дорівнює 24 см. Його довжина у 2 рази більша, ніж ширина. Побудуй цей прямокутник. Знайди його площу.
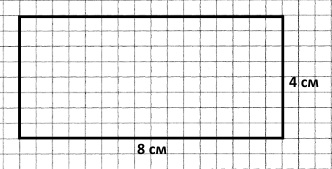
1) 24 : 2 = (20 + 4) : 2 = 12 (см) – півпериметр (сума довжини і ширини).
Якщо довжина у 2 рази більша за ширину, то на довжину припадає 2 частини, а на ширину – одна, тому
2) 12 : 3 = 4 (см) – ширина прямокутника (1 частина).
3) 4 • 2 = 8 (см) – довжина прямокутника (2 частини).
S = 8 • 4 = 32 (см2)
2 спосіб (алгебраїчний)
Нехай х (см) – ширина прямокутника, х • 2 (см) – довжина прямокутника.
Складемо рівняння:
(х • 2 + х) • 2 = 24
х • 2 + х = 24 : 2
х • (2 + 1) = 12
х • 3 = 12
х = 12 : 3 = 4 (см) – ширина прямокутника.
х • 2 = 4 • 2 = 8 (см) – довжина прямокутника.
S = 8 • 4 = 32 (см2)
До № 370 – 379
Завдання 1 Ділення з остачею
|
36 : 8 = 4 (ост. 4) |
5 : 9 = 0 (ост. 5) |
378 : 10 = 37 (ост. 8) |
|
2670 : 10 = 267 |
500360 : 1000 = 500 (ост. 360) |
|
Завдання 2 Ділення
Ділення перевіряємо множенням і діленням
|
_35146 | 7 35 5020 (ост. 6) _14 14 6 (ост. ) |
х5020 7 35140 |
+35140 6 35146 |
_28016 | 4 28 7004 _16 16 0 |
х7004 4 28016 |
Завдання 3 Складена задача на різницеве порівняння
Висота надводної частини айсберга 12 м. Це — частина 1/6 частина висоти всього айсберга. На скільки метрів підводна частина айсберга більша від висоти його надводної частини?
|
Короткий запис Надводна — 12 м, 1/6 всього Підводна — ?; на ? м більше, ніж надводна Всього — ? |
|
Вираз (12 • 6 – 12) – 12
Розв’язання
Якщо 12 м – це вже дріб 1/6 від усього, тоді
1) 12 • 6 = (10 + 2) • 6 = 72 (м) – висота айсберга.
2) 72 – 12 = 60 (м) – висота підводної частини.
3) 60 – 12 = 40 + 20 – 12 = 48 (м) – на стільки метрів підводна частина айсберга більша від висоти його надводної частини.
2 спосіб
Якщо 1/6 – це надводна частина айсберга, тобто айсберг має 6 частин, а над водою 1 частина, тоді під водою – 5 таких частин, тому
1) 5 – 1 = 4 (ч.) – на стільки частин підводна частина айсберга більша від висоти його надводної частини.
2) 12 • 4 = (10 + 2) • 4 = 48 (м) – на стільки метрів підводна частина айсберга більша від висоти його надводної частини.
Відповідь: на 48 метрів підводна частина айсберга більша від висоти його надводної частини.
Сторінка 68
Завдання 4
Побудуй прямокутник площею 16 см2, який можна розділити на 4 рівні квадрати. Знайди периметр прямокутника і одного квадрата.
16 = (2 • 4) • 2 Маємо прямокутник довжиною 8 см і шириною 2 см.
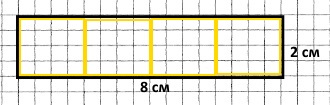
Р = (8 + 2) • 2 = 20 (см) – периметр прямокутника довжиною 8 см і шириною 2 см.
Вийшло 4 квадрати зі стороною 2 см.
S = 2 • 2 = 4 (см2) – площа квадрата зі стороною 2 см.
До № 380 – 400
Завдання 1 Множення та ділення
|
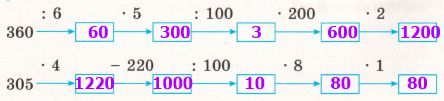
360 : 6 = 36 дес. : 6 = 6 дес. = 60 60 • 5 = 6 дес. • 5 = 30 дес. = 300 300 : 100 = 3 сот. : 1 сот. = 3 3 • 200 = 3 • 2 сот. = 6 сот. = 600 600 • 2 = 6 сот. • 2 = 12 сот. = 1200 |
305 • 4 = (300 + 5) • 4 = 1200 + 20 = 1220 1220 – 220 = 1000 1000 : 100 = 10 10 • 8 = 80 80 • 1 = 80 |
Завдання 2
Катер проплив за течією річки 180 км за 6 год і повернувся назад. Скільки годин плив катер проти течії річки, швидкість якої 5 км/год?
|
tза — 6 год ----------vрічки=5км/год--------------------->∆ tпроти — ? год <------------------------------------------------∆ S = 180 км |
Розв'язання
1) 180 : 6 = 30 (км/год) – швидкість катера за течією річки.
2) 30 – 5 = 25 (км/год) – власна швидкість катера.
3) 25 – 5 = 20 (км/год) – швидкість катера проти течії річки.
4) 180 : 20 = 9 (год) – годин катер плив проти течії річки.
Відповідь: катер плив проти течії 9 годин.
Сторінка 69
Завдання 3
З двох міст, відстань між якими 42 км, виїхали одночасно назустріч один одному два вершники і зустрілися через 2 год. Перший вершник їхав зі швидкістю 12 км/год. З якою швидкістю їхав другий вершник?
|
VІ вершник = 12 км/год t = 2 год VІІ вершник — ? км/год ------------------------------>∆<-------------------------------------------- S = 42 км |
Розв’язання
1 спосіб
План розв’язування
1) Яку відстань проїхав перший вершник? 12 • 2 = 12 + 12 = 24 (км)
2) Яку відстань проїхав другий вершник? 42 – 24 = 42 – 22 – 2 = 18 (км)
3) Яка швидкість другого вершника? 18 : 2 = 9 (км/год)
(42 – 12 • 2) : 2 = 9 (км/год)
2 спосіб
План розв’язування
1) Яка швидкість зближення двох вершників разом? 42 : 2 = 21 (км/год)
2) Яка швидкість другого вершника? 21 – 12 = 21 – 11 – 1 = 9 (км/год)
42 : 2 – 12 = 9 (км/год)
Відповідь: другий вершник їхав зі швидкістю 9 км/год.
Завдання 4 Множення на розрядну одиницю
400 = 4 • 100 5 000 = 5 • 1 000
30 = 3 • 10 200 000 = 2 • 100 000
Завдання 5 Складена задача на знаходження невідомого доданку
Два поїзди їдуть назустріч один одному з двох міст. Один проїхав 80 км, що становить 2/5 відстані між містами, а другий — половину відстані між містами. Скільки кілометрів залишилося проїхати поїздам до зустрічі?
Розв'язання
Короткий запис
І поїзд — 80 км, це 2/5 всього
ІІ поїзд — ?, 1/2 від всього
Всього І і ІІ поїзди — ?
Між ними — ?
Всього — ?
Якщо 80 км уже становить дріб 2/5 усієї відстані, тоді
1) 80 : 2 • 5 = 200 (км) – відстань між містами.
2) 200 : 2 = 100 (км) – відстань проїхав другий поїзд.
3) 100 + 80 = 180 (км) – відстань проїхали два поїзди разом.
4) 200 – 180 = 20 (км) – відстань залишилося проїхати до зустрічі.
2 спосіб
Короткий запис
І поїзд — 80 км, це 2/5 всього
ІІ поїзд — ?, 1/2 від всього
Між ними — ?
Всього — ?
Якщо 80 км уже становить дріб 2/5 усієї відстані, тоді
1) 80 : 2 • 5 = 200 (км) – відстань між містами.
2) 200 : 2 = 100 (км) – відстань проїхав другий поїзд.
3) 200 – 80 – 100 = 20 (км) – відстань залишилося проїхати до зустрічі.
Відповідь: до зустрічі залишилось проїхати 20 кілометрів.
Сторінка 70
Завдання 6
Кіт полює на мишку. Йому до неї 5 стрибків, а мишці до нірки – 20 кроків. Поки кіт зробить 1 стрибок, мишка пробіжить 3 кроки. Чи впіймає кіт мишку?
Короткий запис
Кіт — ? кр., 5 стрибків по 3 кроки
Мишка — 20 кроків
Що менше — ?
Розв’язання
1) 3 • 5 = 15 (кр.) – кроків котові до мишки. 15 < 20 Кіт упіймає мишку.
До №401 – 422
Завдання 1

80 • 40 = 8 • 10 • 4 • 10 = 32 • 100 = 3200 3200 : 10 = 320 320 • 100 = 32 000
32 000 : 8 = 32 тис. : 8 = 4 тис. = 4 000 4 000 • 7 = 4 тис. • 7 = 28 тис. = 28 000
Завдання 2 Складена задача на знаходження невідомого доданку
У їдальні за три місяці використали 1224 кг овочів. За перший місяць використали третю частину всіх овочів, за другий — у 2 рази менше, ніж за перший. Скільки кілограмів овочів використали в їдальні за третій місяць?
Короткий запис
І — ?, 1/3 від всього
ІІ — ?, у 2 рази менше, ніж за І
Всього (І і ІІ місяць) — ?
ІІІ — ?
Всього — 1224 кг
1 спосіб
1) 1224 : 3 = (1200 + 24) : 3 = 408 (кг) – кілограмів овочів використали за І місяць.
2) 408 : 2 = (400 + 8) : 2 = 204 (кг) – кілограмів овочів використали за ІІ місяць.
3) 408 + 204 = 612 (кг) – кілограмів овочів використали за перший та другий місяць разом.
4) 1224 – 612 = 1200 – 600 + 24 – 12 = 612 (кг) – кілограмів овочів використали за ІІІ місяць.
2 спосіб
Короткий запис
І — ?, 1/3 від всього
ІІ — ?, у 2 рази менше, ніж за І
ІІІ — ?
Всього — 1224 кг
1) 1224 : 3 = (1200 + 24) : 3 = 408 (кг) – кілограмів овочів використали за І місяць.
2) 408 : 2 = (400 + 8) : 2 = 204 (кг) – кілограмів овочів використали за ІІ місяць.
3) 1224 – 408 – 204 = 1200 – 400 – 200 + 24 – 8 – 4 = 612 (кг) – кілограмів овочів використали за ІІІ місяць.
3 спосіб
Оскільки 1/3 = 2/6, маємо всього 6 частин, з яких 2 частини припадає на І місяць, тому
1) 2 : 2 = 1 (частина) – частин припадає на другий місяць.
3) 6 – 1 – 2 = 3 (частини) – частин припадає на третій місяць.
4) 1224 : 6 • 3 = 612 (кг) – кілограмів овочів використали за третій місяць.
Відповідь за третій місяць використали 612 кілограмів овочів.
* Яку додаткову дію треба буде виконати в задачі, якщо змінити запитання так: на скільки кілограмів овочів витратили більше за третій місяць, ніж за перший?
612 – 408 = 204 (кг) – на стільки кілограмів овочів витратили більше за третій місяць, ніж за перший.