© Барна Р., 2021
Серія "Вчимось разом" до робочого зошита "Математика 4 клас Листопад Н."
Сторінка 51
Завдання 1 Письмове множення
|
х2300 40 92000 |
х2450 300 735000 |
х 4500 70 315000 |
Завдання 2 Ділення способом послідовного ділення
56 000 : 800 = 56 000 : 100 : 8 = 560 : 8 = 70
480000 : 6000 = 480000 : 1000 : 6 = 480 : 6 = 80
3500 : 70 = 3500 : 10 : 7 = 350 : 7 = 50
Завдання 3 Визнач, за який час кожний літальний апарат подолав указану відстань.
|
Транспорт |
Час |
Відстань |
Розв’язання |
|
|
Ракета |
8 км/с |
3 с |
72 км |
72 : 8 = 9 (с) |
|
Вертоліт |
200 км/год |
9 год |
1800 км |
1800 : 200 = 9 (год) |
|
Дрон |
400 м/хв |
23 хв |
9200 м |
9200 : 400 = 23 (хв.) |
72 : 8 = 9 (с) – час ракети.
1800 : 200 = 18 : 2 = 9 (год) – час вертольоту.
9200 : 400 = (80 + 12) : 4 = 23 (хв.) – час дрона.
Сторінка 52
Завдання 1 Складена задача на знаходження суми добутків
Дві мурахи повзли назустріч одна одній через стежку й зустрілися через 5 с. Перша мураха повзла зі швидкістю 4 см/с, а друга — зі швидкістю 6 см/с. Яка ширина стежки?
1 спосіб
|
Комаха |
Швидкість (см/с) |
Час (с) |
Відстань (см) |
|
|
І мураха |
4 |
5 |
? |
? |
|
ІІ мураха |
6 |
5 |
? |
|
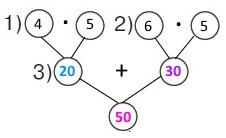
Вираз 4 • 5 + 6 • 5
Розв’язання
1) 4 • 5 = 20 (см) – відстань першої мурахи.
2) 6 • 5 = 30 (см) – відстань другої мурахи.
3) 20 + 30 = 50 (см) – ширина стежки.
2 спосіб
|
Комаха |
Швидкість (см/с) |
Час (с) |
Відстань (см) |
|
|
І мураха |
4 |
|
|
|
|
ІІ мураха |
6 |
|
|
|
|
Всього |
? |
5 |
|
? |
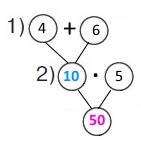
Вираз (4 + 6) • 5
Розв’язання
1) 4 + 6 = 10 (см/с) – швидкість зближення.
2) 10 • 5 = 50 (см) – ширина стежки.
Відповідь: ширина стежки 50 сантиметрів.
Завдання 2 Записали імена дітей на діаграмі, коли відомо, що Іван й Олесь витрачають однаковий час на ранкову зарядку, Остап робить зарядку довше, ніж Ігор.
|
□□□ |
□ |
□□□□ |
□□□ |
|
Іван |
Ігор |
Остап |
Олесь |
Сторінка 53
Завдання 1 Письмове ділення
|
_28920 | 40 280 723 _92 80 _120 120 0 |
_74340 | 90 720 826 _234 180 _540 540 0 |
Завдання 2 Слон і слоненя почали рухатися одночасно назустріч одне одному. Швидкість слона становила 60 м/хв, а швидкість слоненяти — 20 м/хв. Яка відстань була між тваринами спочатку, якщо вони зустрілися через 10 хв?
|
1 спосіб
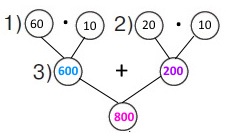
Вираз 60 • 10 + 20 • 10 Розв’язання 1) 60 • 10 = 600 (м) – відстань першого слоненяти. 2) 20 • 10 = 200 (м) – відстань другого слоненяти. 3) 600 + 200 = 800 (см) – відстань була між тваринами спочатку. |
2 спосіб
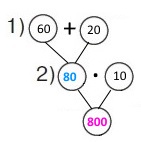
Вираз (60 + 20) • 10 Розв’язання 1) 60 + 20 = 80 (м/хв) – швидкість зближення. 2) 80 • 10 = 800 (м) – відстань була між тваринами спочатку. |
Відповідь: спочатку відстань між тваринами була 800 метрів.
Завдання 3
|
_17700 | 50 15 354 _27 25 _20 20 0 |
_124000 | 500 10 248 _24 20 _40 40 0 |
Сторінка 54
|
Завдання 1 |
Завдання 2 |
||||
|
х 568 43 1704 2272 24424 |
х 3472 22 6944 6944 76384 |
х 2704 49 24336 10816 132496 |
х 480 36 288 144 17280 |
х 790 29 711 158 22910 |
х 2300 47 161 92 108100 |
Завдання 3 З двох міст одночасно назустріч один одному вирушили автобус й автомобіль і зустрілися через 11 год. Яка відстань між містами, якщо швидкість автомобіля дорівнює 80 км/год, а швидкість автобуса — на 20 км/год менша?
1 спосіб
|
Транспорт |
Швидкість (км/год) |
Час (год) |
Відстань (км) |
|
|
Автомобіль |
80 |
11 |
? |
? |
|
Автобус |
?, на 20 км/год менше |
11 |
? |
|
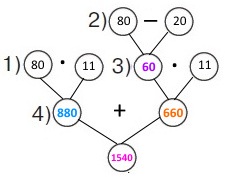
Вираз 80 • 11 + (80 – 20) • 100
Розв’язання
1) 80 • 11 = 800 + 80 = 880 (км) – відстань автомобіля.
1) 80 – 20 = 60 (км/год) – швидкість автобуса.
2) 60 • 11 = 600 + 60 = 660 (км) – відстань автобуса.
3) 880 + 660 = 880 + 700 – 40 = 1540 (км) – відстань між містами.
2 спосіб
|
Транспорт |
Швидкість (км/год) |
Час (год) |
Відстань (км) |
|
|
Автомобіль |
80 |
|
|
|
|
Автобус |
?, на 20 км/год менше |
|
|
|
|
Всього |
? |
5 |
|
? |
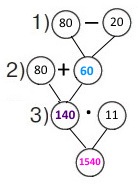
Вираз (80 + (80 – 20) ) • 5
Розв’язання
1) 80 – 20 = 60 (км/год) – швидкість автобуса.
1) 80 + 60 = 80 + 20 + 40 = 140 (км/год) – швидкість зближення.
2) 140 • 11 = 1400 + 140 = 1540 (км) – відстань між містами.
Відповідь: відстань між містами 1540 кілометрів.
Сторінка 55
Завдання 1
|
х 346 237 2422 1038 692 82002 |
х 794 363 2382 4764 2382 288222 |
х 2306 124 9224 4612 2306 285944 |
Завдання 2
|
Транспорт |
Швидкість |
Час |
Відстань |
Розв’язання |
|
Потяг |
85 км/год |
12 год |
1020 км |
х 85 12 170 85 1020 (км) |
|
Автобус |
75 км/год |
5 год |
375 км |
х 75 5 375 (км) |
|
Автомобіль |
110 км/год |
7 год |
770 км |
х110 7 770 (км) |
Завдання 3
|
Тварина |
Швидкість |
Час |
Відстань |
Розв’язання |
|
Кінь |
8 км/год |
2 год |
10 км |
10 : 5 = 2 (год) |
|
Собака |
10 км/год |
однаковий |
20 км |
20 : 2 = 10 (км/год) |
|
Лисиця |
20 км/год |
однаковий |
40 км |
40 : 2 = 20 (км/год) |
|
Заєць |
30 км/год |
однаковий |
60 км |
60 : 2 = 30 (км/год) |
Завдання 4 Обчислили значення виразу
Якщо с = 852, тоді с : 3 + с • 126 = 852 : 3 + 852 • 126 = 284 + 107352 = 107636
|
_852 | 3 6 284 _25 24 _12 12 0 |
х 852 126 5112 1704 852 107352 |
+107352 284 107636 |
Сторінка 56
Завдання 1
|
х 2305 342 4610 9220 6915 788310 |
х 3047 317 21329 3047 9141 965899 |
х 2005 453 6015 10025 8020 908265 |
Завдання 2
Циліндр, конус, піраміда, круг, паралелепіпед.
Завдання 3
|
х 365 205 1825 730 74825 |
х 678 706 4068 4746 478668 |
х 3709 209 33381 7418 775181 |
Завдання 4 Одиниці вимірювання
24 год = 1 год • 24 = 60 хв • 24 = 1440 хв
17 год = 1 год • 17 = 60 хв • 17 = 1020 хв
120 с = (120 : 60) хв = (12 : 6) хв. = 2 хв
13 год 15 хв = 1 год • 13 + 15 хв = 60 хв • 13 + 15 хв = 780 хв + 15 хв = 795 хв
|
х24 60 1440 |
х17 60 1020 |
х13 60 780 |
+780 15 795 |
Сторінка 57
Завдання 1
|
х 3064 124 12256 6128 3064 379936 |
х 1007 227 7049 2014 2014 228589 |
х 218 903 654 1962 196854 |
Завдання 2 Складена задача на зведення до одиниці
За 7 однакових плиток шоколаду заплатили 161 грн. Яка вартість чотирьох таких плиток шоколаду? Яка вартість трьох таких плиток шоколаду?
|
Ціна (грн) |
Кількість |
Вартість (грн) |
|
? |
7 |
161 грн |
|
однакова |
4 |
? |
|
однакова |
3 |
? |
Короткий запис
7 шоколадок — 161 грн
4 шоколадки — ? грн
3 шоколадки — ? грн
План розв’язування
1) Яка маса одної плитки шоколаду?
2) Яка маса чотирьох таких плиток шоколаду?
3) Яка маса трьох таких плиток шоколаду?
Розв’язання
1) 161 : 7 = (140 + 21) : 7 = 20 + 3 = 23 (грн) – ціна плитки шоколаду.
2) 23 • 4 = (20 + 3) • 4 = 80 + 12 = 92 (грн) – вартість чотирьох плиток шоколаду.
3) 23 • 3 = (20 + 3) • 3 = 60 + 9 = 69 (грн) – вартість трьох таких плиток шоколаду.
2 спосіб
1) 161 : 7 = (140 + 21) : 7 = 20 + 3 = 23 (грн) – ціна плитки шоколаду.
2) 23 • 4 = (20 + 3) • 4 = 80 + 12 = 92 (грн) – вартість чотирьох плиток шоколаду.
3) 161 – 92 = 161 – 100 + 8 = 69 (грн) – вартість трьох таких плиток шоколаду.
Відповідь: 92 гривні, 69 гривень.
Завдання 3 Складена задача на зведення до одиниці
Малинове й абрикосове варення загальною масою 7 кг (7000 г) розфасували в банки, порівну в кожну. Одержали 7 банок з малиновим варенням і 13 — з абрикосовим. Яка маса малинового варення? Яка маса абрикосового варення?
|
Варення |
Маса 1 банки (г) |
Кількість банок |
Загальна маса (г) |
|
Малинове |
однакова |
7 |
? |
|
Абрикосове |
однакова |
13 |
? |
|
Всього |
? |
? |
7000 |
План розв’язування
1) Скільки всього банок з варенням?
2) Яка маса одної банки з варенням?
3) Яка маса малинового варення?
4) Яка маса абрикосового варення?
Розв’язання
1) 7 + 13 = 20 (б.) – всього банок з варенням.
2) 7000 : 20 = 700 : 2 = (600 + 100) : 2 = 350 (г) – маса одної банки з варенням.
3) 350 • 7 = (300 + 50) • 7 = 2100 + 350 = 2450 (г) = 2 кг 450 г
4) 350 • 13 = 4550 (г) = 4 кг 550 г
Відповідь: 2 кг 450 г, 4 кг 550 г
Сторінка 58
Завдання 1 Ділення з остачею
141 : 23 = 6 (ост. 3) 565 : 56 = 10 (ост. 5)
|
_141 |23 138 6 (ост. 3) 3 |
_565 | 56 56 10 (ост. 5) _5 0 5 |
Завдання 2 Цифр у частці
|
Вираз на ділення |
4736 : 37 |
5248 : 64 |
20176 : 97 |
668 : 78 |
|
Перша неповна частка |
47 |
524 |
201 |
668 |
|
Залишилось цифр |
2 |
1 |
2 |
0 |
|
Цифр у частці |
3 |
2 |
3 |
1 |
Завдання 3
|
_86020 | 34 68 2530 _180 170 _102 102 0 |
_45600 | 38 38 1200 _76 76 0 |
Завдання 4 Доповнили чотирикутник до квадрата зі стороною 3 см. Обчисли периметр і площу утвореного квадрата.
Р = 3 • 4 = 12 (см) – периметр квадрата зі стороною 3 см.
S = 3 • 3 = 9 (см2) – площа квадрата зі стороною 3 см.
Сторінка 59
|
Завдання 1 |
Завдання 2 |
||
|
_15300 | 34 136 450 _170 170 0 |
_54810 | 63 504 870 _441 441 0 |
_7038 | 34 68 207 _23 0 _238 238 0 |
_14558 | 29 145 502 _5 0 _58 58 0 |
Завдання 3 Рівняння
|
с • 36 = 4428 с = 4428 : 36 с = 123 123 • 36 = 4428 4428 = 4428 |
_4428 | 36 36 123 _82 72 _108 108 0 |
х123 36 738 369 4428 |
Завдання 4 Складена задача на множення
Автотуристи рухалися з однаковою швидкістю і через З год зробили зупинку для відпочинку. Потім вони продовжили рух і їхали ще 2 год. Яку відстань проїхали туристи до зупинки, якщо весь шлях становив 420 км?
|
|
Швидкість (км/год) |
Час (год) |
Відстань (км) |
|
спочатку |
однакова |
3 |
? |
|
потім |
однакова |
2 |
|
|
Всього |
? |
? |
420 км |
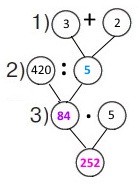
Вираз (420 : (3 + 2)) • 3
План розв’язування
1) Скільки всього часу були в дорозі?
2) Яка швидкість туристів?
3) Яку відстань проїхали туристи до зупинки?
Розв’язання
1) 3 + 2 = 5 (год) – всього часу були в дорозі.
2) 420 : 5 = (300 + 100 + 20) : 5 = 84 (км/год) – швидкість туристів.
3) 84 • 3 = (80 + 4) • 3 = 240 + 12 = 252 (км) – відстань проїхали туристи до зупинки.
Відповідь: до зупинки туристи проїхали 252 кілометри.
Сторінка 60
|
Завдання 1 |
Завдання 2 |
||
|
_188752 | 94 188 2008 _752 752 0 |
_109120 | 64 64 1705 _451 448 _320 320 0 |
_35175 | 25 25 1407 _101 100 _175 175 0 |
х1407 25 7035 2814 35175 |
Завдання 3
Макар купив в автоматі 12 л води, а Олеся — 8 л. Макар заплатив за воду на 4 грн більше, ніж Олеся. Скільки гривень заплатив за воду кожний з дітей?
|
Діти |
Ціна (грн) |
Кількість (л) |
Вартість (грн) |
|
Макар |
? |
12, на ? л більше |
?, на 4 грн більше |
|
Олеся |
однакова |
8 |
? |
План розв’язування
1) На скільки більше літрів води купив Макар?
2) Яка ціна 1 літри води?
3) Скільки гривень заплатив за воду Макар?
4) Скільки гривень заплатила за воду Олеся?
Розв’язання
1) 12 – 8 = 4 (л) – на стільки більше літрів води купив Макар.
2) 4 : 4 = 1 (грн) – ціна 1 літра води.
3) 1 • 12 = 12 (грн) – гривень заплатив Макар.
4) 1 • 8 = 8 (грн) – гривень заплатила Олеся.
Відповідь: Макар заплатив 12 грн, Олеся – 8 грн.
Завдання 4 Записали три розв'язки нерівності х + 320 < 1000
|
1 спосіб (розв’язування) х + 320 < 1000 х + 320 < 680 + 320 х < 680 |
2 спосіб (добором) 1 + 320 < 1000 (підходить) 10 + 320 < 1000 (підходить) 100 + 320 < 1000 (підходить) |
х1 = 1, х2 = 10, х3 = 100