ГДЗ робочий зошит Лишенко 4 клас сторінка 54 – 62 нова програма 2021 року

Інші завдання дивись тут...

Серія "Вчимось разом" до робочого зошита "Математика 4 клас Лишенко Г."

Сторінка 54

Завдання 1 Дії з величинами

8 кг 100 г

_7 кг 1100 г

2 кг 500 г

5 кг 600 г

+51 т 4 ц

8 т 9 ц

59 т 13 ц

60 т 3 ц

+32 доби 15 год

6 діб 38 год

38 діб 53 год

40 діб 5 год

Завдання 2 Складена задача на знаходження чисел за трьома сумами

У вагоні метро їхало 236 пасажирів. Чоловіків і жінок було 208, чоловіків і дітей – 130. Скільки дітей, жінок і чоловіків окремо їхало у вагоні метро?

^{Короткий запис}

^{Жінок і чоловіків — 208 пасажирів}

^{Чоловіків і дітей — 130 пасажирів}

^{Всього жінок, чоловіків, дітей — 236 осіб}

^{Дітей —}^?^{Чоловіків —}^?^{Жінок —}^?

Розв’язання

1) 236 – 208 = 36 – 8 = 28 (д.) – дітей.

2) 130 – 28 = 102 (ч.) – чоловіків.

3) 208 – 102 = 106 (ж.) – жінок.

Відповідь: їхало 28 дітей, 106 жінок, 102 чоловіків.

Завдання 3

24 серпня 1991 року Верховна Рада України ухвалила Акт проголошення незалежності України. Скільки часу минуло з дня прийняття цього важливого документа?

2023 – 1991 = 23 + (2000 – 1991) = 23 + 9 = 23 + 7 + 2 = 32 (роки)

Завдання 4 Одиниці вимірювання

8 т – 35 кг = 7 т 965 кг	^{8 т – 35 кг = 7 т + 1000 кг – 35 кг = 7 т 965 кг}
18 км – 650 м = 17 км 350 м	^{18 км – 17 км 350 м = 1 км – 350 м = 650 м}
З год 25 хв + 45 хв = 5 год – 50 хв	^{3 год 25 хв + 45 хв = 3 год 70 хв = 4 год 10 хв} ^{5 год – 4 год 10 хв = 50 хв}
6 кг 750 м = 5 кг + 1750 м	^{6 кг 750 м – 5 кг = 1 кг 750 м = 1750 м}

Завдання 5

У зоопарку є змії, качки й мавпочки. Вони мають 36 голів 26 крил і 86 лап. Скільки змій у зоопарку?

Розв’язання

1) 26 : 2 = 13 (к.) – качок (у качок по 2 крила).

2) 2 • 13 = 26 (л.) – лап у качок.

3) 86 – 26 = 60 (л.) – лап у мавпочок.

4) 60 : 4 = (40 + 20) : 4 = 15 (м.) – мавпочок.

5) 13 + 15 = 28 (тв.) – всього качок і мавпочок.

6) 36 – 28 = 6 + (30 – 28) = 8 (з.) – змій у зоопарку.

Відповідь: у зоопарку 8 змій.

Сторінка 55 До № 151 – 171

Завдання 1 Письмове віднімання

_600

521

_7000

2907

4093

_40200

28092

12108

_31002

20297

10705

Завдання 2

Скутерист за З год проїхав 108 км. За цей час велосипедист проїхав відстань, у З рази меншу. З якою швидкістю їхав велосипедист?

1 спосіб

1) 108 : 3 = (90 + 18) : 3 = 36 (км) – відстань проїхав велосипедист за 3 год.

2) 36 : 3 = (30 + 6) : 3 = 12 (км/год) – швидкість велосипедиста.

2 спосіб

1) 108 : 3 = 36 (км/год) – швидкість скутериста.

2) 36 : 3 = 12 (км/год) – швидкість велосипедиста.

Відповідь: швидкість велосипедиста 12 км/год.

Завдання 3 Нерівності

5 < а ≤ 11	286 ≤ b < 292	36 789 < с < 36 795
а=6,7,8,9,10,11	b=286,287,288,289,290,291	с=36790, 36791, 36792, 36793, 36794

Завдання 4

Швидкість течії річки 2 км/год. Теплохід за 6 год проплив за течією 168 км, а потім повернувся назад. За скільки годин теплохід повернувся назад?

Розв’язання

1) 168 : 6 = (120 + 48) : 6 = 28 (км/год) – швидкість теплохода за течією річки.

2) 28 – 2 = 26 (км/год) – власна швидкість теплохода (у стоячій воді).

3) 26 – 2 = 24 (км/год) – швидкість теплохода проти течії річки.

4) 168 : 24 = 7 (год) – час на зворотному шляху.

Відповідь: теплохід повернувся через 7 годин.

Завдання 5

Із 13 кг яблук отримали а л соку. Скільки соку можна одержати із 520 кг яблук? Склади вираз. Обчисли, якщо а = 7.

^{План розв’язування}

^{У скільки разів більше яблук – у стільки разів більше соку можна одержати.}

^{1) У скільки разів більше яблук? 520 : 13 (разів)}

^{2) Скільки соку можна одержати? а • (520 : 13) (л)}

а • (520 : 13) (л) – літрів соку можна одержати.

Якщо а = 7, тоді а • (520 : 13) = 7 • 40 = 280 (л)

Сторінка 56 До № 172 – 193

Завдання 1 Порядок дій

2 • 386 • 5 • 10 = 386 • 10 • 10 = 386 • 100 = 38600

2356 • 4 • 25 : 10 = 2356 • 100 : 10 = 235600 : 10 = 23560

245 • 3 + 7 • 245 = 245 • (3 + 7) = 245 • 10 = 2450

Завдання 2 Складена задача на знаходження суми добутків

Туристи спочатку їхали 2 год поїздом зі швидкістю 60 км/год, а потім З год йшли пішки зі швидкістю 4 км/год. Чому дорівнює весь шлях, подоланий туристами?

^{Короткий запис}

^{Спочатку —}^?^{км, 2 год по 60 км/год}

^{Потім —}^?^{км, 3 год по 4 км/год}

^{Всього (відстань) —}^?

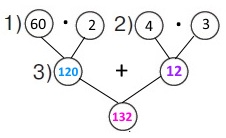
^{Вираз 60 • 2 + 4 • 3}

Розв’язання

1) 60 • 2 = 120 (км) – відстань спочатку.

2) 4 • 3 = 12 (км) – відстань потім.

3) 120 + 12 = 132 (км) – весь шлях.

Відповідь: весь шлях дорівнює 132 кілометри.

Змінили запитання задачі так, щоб останньою дією в розв'язанні було віднімання.

У скільки разів більше пройшли першого дня, ніж другого?

3) 120 : 12 = 10 (разів)

^{У скільки разів менше пройшли другого дня, ніж першого?}

^{3) 120 : 12 = 10 (разів)}

^{На скільки кілометрів більше пройшли першого дня, ніж другого?}

^{3) 120 – 12 = 100 + (20 – 12) = 108 (км)}

^{На скільки кілометрів менше пройшли другого дня, ніж першого?}

^{3) 120 – 12 = 100 + (20 – 12) = 108 (км)}

Завдання 3

Відстань між двома містами 75 км. Третину цієї відстані поїзд подолав за 25 хв. З якою швидкістю рухався поїзд? Розв'яжи задачу складанням виразу.

^{План розв’язування}

^{1) Яку відстань подолав поїзд? 75 : 3 = (60 + 15) : 3 = 25 (км)}

^{2) З якою швидкістю рухався поїзд? 25 : 25 = 1 (км/хв)}

Розв’язання

(75 : 3) : 25 = 1 (км/хв)

Відповідь: поїзд рухався зі швидкістю 1 км/хв.

Сторінка 57

Завдання 4 Письмове множення

х25068

175476

х320578

2244046

х107283

643698

Завдання 5

У класі 7 дітей відвідують спортзал щодня. 9 – відвідують через день, а решта – взагалі не відвідують. Учора в спортзалі займалось 13 дітей цього класу. Скільки дітей прийдуть у спортзал сьогодні?

^{Міркуємо так. Кожного дня приходить 7 дітей, 7 + 9 = 16 (д.) – щонайбільше дітей може прийти через день. Якщо учора займалося 13 дітей, то сьогодні прийде не більше 7 дітей.}

Відповідь: не більше 7 дітей.

До № 194 – 216

Завдання 1

х3275

13100

х24036

168252

х328204

984612

х6500

26000

х20030

120180

х58004

464032

Завдання 2 Складена задача на ділення на вміщення

90 т вугілля одна вантажівка може перевезти за 15 рейсів, а друга — за 10 рейсів. За скільки рейсів перевезуть це вугілля вантажівки, якщо працюватимуть разом?

	^{Маса за 1 рейс (т)}	^{Кількість рейсів}	^{Загальна маса (т)}
^{І вантажівка}	^?	¹⁵	⁹⁰
^{ІІ вантажівка}	^?	¹⁰	^{однаково}
^Всього	^?	^?	⁹⁰

Розв’язання

1) 90 : 15 = 90 : 3 : 5 = 6 (т) – масу за 1 рейс перевозить І вантажівка.

2) 90 : 10 = 9 (т) – масу за 1 рейс переводить ІІ вантажівка.

3) 6 + 9 = 15 (т) – масу за 1 рейс перевозять вантажівки разом.

4) 90 : 15 = 90 : 3 : 5 = 6 (р.) – рейсів потрібно зробити.

Відповідь: разом перевезуть за 6 рейсів.

Сторінка 58

Завдання 3

Зі села до міста автомобіль їхав 3 год зі швидкістю 56 км/год. Назад він повернувся за 2 год. З якою швидкістю автомобіль їхав на зворотному шляху?

^{Швидкість}	^Час	^{Відстань}
^{56 км/год}	^{3 год}	^?
^?	^{2 год}	^{однакова}

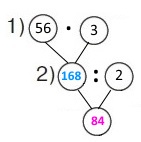
^{Вираз (56 : 3) : 2}

Розв’язання

1) 56 • 3 = (50 + 6) • 3 = 168 (км) – відстань між селом і містом.

2) 168 : 2 = (160 + 8) : 2 = 84 (км/год) – швидкість автомобіля на зворотному шляху.

Відповідь: автомобіль їхав зі швидкістю 84 км/год.

Завдання 4

Всі одноцифрові числа, які є розв’язками нерівностей.

^{180 : х < 40}

^{180 : х < 45}

^{180 : х < 180 : 4}

^{х > 4}

^{а • 20 > 125}

^{а • 20 > 6 • 20}

^{а > 6}

^{b : 2 ≤ 5}

^{b : 2 ≤ 10 : 2}

^{b ≤ 10}

х = 5, 6, 7, 8, 9

а = 7, 8, 9

b = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Завдання 5

На стадіон прийшло 7 хлопчиків і 6 дівчаток. Пізніше до них підійшло ще декілька дітей. Усі діти розділилися на 2 з однаковою кількістю учасників. У кожній команді кількість дівчаток і кількість хлопчиків однакова. Яка найменша кількість дітей, що підійшли на стадіон пізніше?

^{Міркуємо так. (7 + 1) : 2 = 4, (6 + 2) : 2 = 4. Щонайменше могло підійти 1 хлопчик і 2 дівчинки. Усього 3 дітей.}

Відповідь: підійшло 3 дітей.

До № 217 – 239

Завдання 1

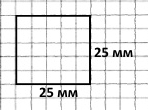
Периметр трикутника, у якого всі сторони рівні, 7 см 5 мм. Побудуй квадрат, довжина сторони якого дорівнює довжині сторони трикутника. Знайди його периметр.

Розв’язання

1) 7 см 5 мм = 75 мм

75 : 3 = (60 + 15) : 3 = 25 (мм) – довжина сторони рівностороннього трикутника.

2) Р = 25 • 4 = (20 + 5) • 4 = 100 (мм) = 10 (см)

Сторінка 59

Завдання 2

^{4800 : 10 = 480}

^{480 : 3 = (300 + 180) : 3 = 100 + 60 = 160}

^{160 • 8 = (100 + 60) • 8 = 800 + 480 = 1280}

^{1280 + 140 = 1000 + 300 + 120 = 1420}

^{1000 – 360 = 600 + (400 – 360) = 640}

^{640 : 10 = 64}

^{64 : 8 = 8}

^{8 • 0 = 0}

^{640 : 20 = (600 + 40) : 20 = 30 + 2 = 32}

^{32 • 100 = 3200}

^{3200 + 400 = 3600}

^{3600 : 10 = 360}

^{2360 – 2060 = 300}

^{300 : 2 = (200 + 100) : 2 = 100 + 50 = 150}

^{150 • 10 = 1500}

^{1500 + 150 = 1650}

Завдання 3 Складена задача на ділення на вміщення

Одна бригада може виготовити 360 деталей за 12 днів, а друга – за 6 днів. За скільки днів буде виготовлено 360 деталей, якщо бригади працюватимуть разом?

^{Бригада}	^{Деталей за 1 день} ^{(продуктивність праці)}	^{Кількість днів} ^{(час роботи)}	^{Загальна кількість деталей} ^{(загальний виробіток)}
^І	^?	¹²	³⁶⁰
^ІІ	^?	⁶	^{однаково}
^Всього	^?	^?	³⁶⁰

Розв’язання

1) 360 : 12 = 360 : 6 : 2 = 30 (д.) – деталей виготовляє І бригада за 1 день.

2) 360 : 6 = 60 (д.) – деталей виготовляє ІІ бригада за 1 день.

3) 30 + 60 = 90 (д.) – деталей виготовляють І і ІІ бригада разом за 1 день.

4) 360 : 90 = 36 : 9 = 4 (дн.) – днів працюватимуть.

Відповідь: буде виготовлено за 4 дні.

Завдання 4

Усі одноцифрові числа — розв'язки нерівностей.

^{150 : х < 60}

^{150 : х < 75}

^{150 : х < 150 : 2}

^{х > 2}

^{с • 30 > 125}

^{с • 30 > 120}

^{с • 30 > 4 • 30}

^{с > 4}

^{b : 3 ≤ 6}

^{b : 3 ≤ 18 : 3}

^{b ≤ 18}

х = 3,4,5,6,7,8,9

с =5, 6, 7, 8, 9

b = 0,1,2,3,4,5,6,7,8,9

Завдання 5

Сума двох чисел 876, а їх різниця — 224. Знайди ці числа.

^{Міркуємо так. а +}^{b = 876}^,^a^–^b^{= 224, тоді знайдемо суму цих рівностей}

(а + b) + (а – b) = 876 + 224

2 • а = 1100

а = 1100 : 2 = (1000 + 100) : 2 = 550 – перше число.

b = 876 – а = 876 – 550 = 326 – друге число.

Відповідь: ці числа 550 і 326.

До № 240 – 261

Завдання 1

^{70 • 90 = 7 • 9 • 100 = 6300}

^{6300 : 100 = 63}

^{63 • 5 = (60 + 3) • 5 = 300 + 15 = 315}

^{315 + 85 = 300 + 90 + 10 = 400}

^{900 : 300 = 9 : 3 = 3}

^{3 • 70 = 210}

^{210 – 40 = 210 – 10 – 30 = 200 – 30 = 170}

^{170 • 5 = (100 + 70) • 5 = 500 + 350 = 850}

^{400 : 8 = 50}

^{50 • 9 = 45 • 10 = 450}

^{450 : 3 = (300 + 150) : 3 = 100 + 50 = 150}

^{150 • 6 = (100 + 50) • 6 = 600 + 300 = 900}

^{850 • 8 = (800 + 50) • 8 = 6400 + 400 = 6800}

^{6800 : 50 = (5000 + 1500 + 300) : 50 = 100 + 30 + 6 = 136}

^{136 • 200 = (100 + 30 + 6) • 200 = 20000 + 6000 + 1200 = 27200}

^{27200 : 5 = (20000 + 5000 + 2000 + 200) : 5 =}

^{= 4000 + 1000 + 400 + 40 = 5440}

Сторінка 60

Завдання 2

(48 512 : 8 – 5 032) : 4 = 258

_48512 | 8

48 6064

_51

_32

_6064

5032

1032

_1032 | 4

8 254

_23

_32

Завдання 3 Складена задача на віднімання

На двох складах було 6080 кг зерна. Коли з першого складу видали 820 кг, а з другого – у 4 рази більше, то на другому складі нічого не залишилося. Скільки кілограмів зерна залишилося на першому складі?

Розв’язання

1) 820 • 4 = (800 + 20) • 4 = 3280 (кг) – зерна видали з ІІ складу.

2) 820 + 3280 = 3000 + 1000 + 100 = 4100 (кг) – всього зерна видали.

3) 6080 – 4100 = 6080 – 5000 + 900 = 1980 (кг) – зерна залишилось на І складі.

Відповідь: на першому складі залишилося 1980 кілограмів зерна.

Завдання 4 Порівняння чисел

1) 486 • 9 > 435 • 9

^{де більший множник, там більший добуток}

8 • 1046 < 4092 • 4

^{2 • 1046 • 4 < 4092 • 4}

х486

4374

х435

3915

х1046

8368

х4092

16368

357 • 6 < 457 • 5

^{де менший множник, там менший добуток}

7200 • 3 = 6 • 3600

^{7200 • 3 = 3600 • 2 • 3}

х357

2142

х457

2285

х7200

21600

х3600

21600

Сторінка 61

Завдання 5

Матері 32 роки, одній з її доньок 8 років, а іншій – 6. Через скільки років вік матері дорівнюватиме сумі років дочок?

1) 8 + 6 = 14 (р.) – сума років дітей.

2) 32 – 14 = 18 (р.)

^{Нехай х (р.) – пройде років, тоді х + 8 + х + 6 (р.) – років стане дітям, 32 + х (р.) – років стане матері. Складемо рівняння.}

^{8 + х + 6 + х = 32 + х}

^{14 + х + х = 32 + х}

^{х + х – х = 32 – 14}

^{х = 32 – 14}

^{х = 18 (р.)}

Відповідь: через 18 років.

До №262 – 283

Завдання 1 Ділення

а	96	128	48	600	126	64	0
b	6	8	4	2	18	16	9
а : b	16	16	12	300	7	4	0

^{96 : 6 = (60 + 36) : 6 = 10 + 6 = 16 16 • 8 = (10 + 6) • 8 = 80 + 48 = 128 48 : 4 = (40 + 8) : 4 = 10 + 2 = 12}

^{600 : 2 = 300 18 • 7 = (10 + 8) • 7 = 70 + 56 = 126 64 : 4 = (40 + 24) : 4 = 10 + 6 = 16 0 : 9 = 0}

Завдання 2 Ділення з остачею

10 дес. : 3 = 100 : 3 = 33 (ост. 1) перевірка 33 • 3 + 1 = 99 + 1 = 100 = 10 дес.

42 : 5 = 8 (ост. 2) перевірка 8 • 5 + 2 = 40 + 2 = 42

1 сот. : 3 = 100 : 3 = 33 (ост. 1) перевірка 33 • 3 + 1 = 99 + 1 = 100 = 1 сот.

Завдання 3 Письмове ділення

2296 : 8 = 287 2086 : 7 = 298 3714 : 6 = 619

_2296 | 8

16 287

_69

_56

х287

2296

_2086 | 7

14 298

_68

_56

х298

2086

_3714 | 6

36 619

_11

_54

х619

3714

Завдання 4 Складена задача на різницеве порівняння часток

У швейній майстерні з 320 м тканини пошили костюми та зі 180 м тканини — сорочки. На кожен костюм витрачали 4 м тканини, а на сорочку — З м. Чого більше пошили і на скільки?

^{Короткий запис}

^{320 м — це}^?^{костюмів по 4 м}

^{180 м — це}^?^{сорочок по 3 м}

^На^?^більше

Розв’язання

1) 320 : 4 = 80 (к.) – костюмів пошили.

2) 180 : 3 = 60 (с.) – сорочок пошили.

3) 80 > 60 костюмів пошили більше.

80 – 60 = 20 (к.) – на стільки більше пошили костюмів, ніж сорочок.

Відповідь: на 2 костюмів більше пошили, ніж сорочок.

Сторінка 62

Завдання 5