Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 23 Коло, вписане в трикутник, властивість бісектриси кута
Завдання 657
Коло, вписане у трикутник, зображено на малюнку 23.3.
Завдання 658
Накресліть гострокутний трикутник. За допомогою транспортира, циркуля і лінійки побудуйте коло, вписане в трикутник.
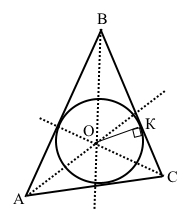
∆ АВС – гострокутний.
ВО – бісектриса кута В трикутника (проведена до сторони до сторони АС), АО – бісектриса кута А (проведена до сторони ВС), СО – бісектриса кута С (проведена до сторони АВ).
Точка О – точка перетину бісектрис трикутника, центр вписаного кола.
ОК – перпендикуляр до сторони ВС, ОК ﬩ ВС.
ОК – радіус вписаного кола.
Завдання 659
Накресліть прямокутний трикутник. За допомогою транспортира, циркуля і лінійки побудуйте коло, вписане в цей трикутник.
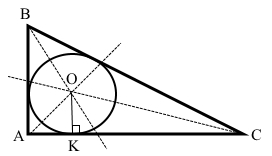
∆ АВС – тупокутний.
ВО – бісектриса кута В трикутника (проведена до сторони до сторони АС), АО – бісектриса кута А (проведена до сторони ВС), СО – бісектриса кута С (проведена до сторони АВ).
Точка О – точка перетину бісектрис трикутника, центр вписаного кола.
ОК – перпендикуляр до сторони ВС, ОК ﬩ ВС.
ОК – радіус вписаного кола.
Завдання 660 Малюнок 23.1
У ∆ABC вписано коло із центром у точці I. Знайдіть кути трикутника ABC, якщо ∠IBK = 35°, ∠MCI = 25°.
За умовою BІ – бісектриса кута В, тому ∠В = 2∠IBK = 35° • 2 = 70°.
За умовою СІ – бісектриса кута С, тому ∠С = 2∠МСІ = 25° • 2 = 50°.
За теоремою про суму кутів трикутника ∠А = 180° – (∠В + ∠С) = 180° – (70° + 50°) = 60°.
Відповідь: 60°, 70°, 50°.
Завдання 661
У ∆ABC вписано коло із центром у точці I. ∠CAB = 70°, ∠CBA = 60°. Знайдіть ∠MCI.
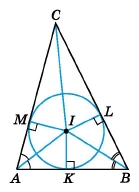
За умовою СІ – бісектриса кута ∠С, тому ∠С = 2∠МСІ.
За теоремою про суму кутів трикутника ∠С = 180° – (∠САВ + ∠САВ) = 180° – (70° + 60°) = 50°.
∠МСІ = ∠С : 2 = 50° : 2 = 25°.
Відповідь: 25°.
Завдання 662
Точка I – центр кола, вписаного в різносторонній трикутник ABC, M, K і L – точки дотику. Знайдіть усі пари рівних між собою трикутників на цьому малюнку.

Відрізки ІМ, ІL, ІК – перпендикуляри до сторін трикутника, тому ∠CLI = ∠BLI = ∠BKI = ∠AKI = ∠AMI = ∠CMI = 90°.
Прямокутні трикутники ∆МСI = ∆LCI, оскільки СІ – бісектриса кута С, ∠МСІ = ∠LСI, СІ – спільна гіпотенуза (за гіпотенузою і гострим кутом).
Прямокутні трикутники ∆LBI = ∆KBI, оскільки BІ – бісектриса кута B, ∠LBI = ∠KBI, BІ – спільна гіпотенуза (за гіпотенузою і гострим кутом).
Прямокутні трикутники ∆KAI = ∆MAI, оскільки AІ – бісектриса кута A, ∠KAІ = ∠MAI, AІ – спільна гіпотенуза (за гіпотенузою і гострим кутом).
Відповідь: маємо три пари рівних трикутників.
Завдання 663
Доведіть, що центр кола, яке дотикається до сторін кута, лежить на бісектрисі кута.
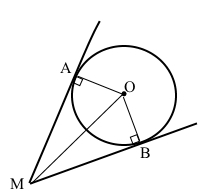
За умовою коло з центром в точці О дотикається до сторін кута М, тоді ОА = ОВ – радіуси кола, згідно властивості відрізків дотичних до кола, проведених з однієї точки, МА = МВ. МО – спільна сторона. За трьома сторонами ∆АМО = ∆ВМО, тому рівні відповідні кути ∠АМО = ∠ВМО. За властивістю вимірювання кутів ∠М = ∠АМО + ∠ВМО = 2∠АМО. Отже відрізок МО – бісектриса кута М.
Завдання 664
Накресліть кут градусної міри 110°. За допомогою циркуля, косинця і транспортира впишіть у кут коло довільного радіуса, тобто побудуйте коло, яке дотикається до сторін даного кута.
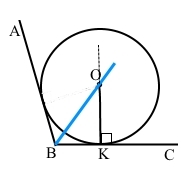
∠АВС = 110°.
ВО – бісектриса кута АВС, ∠ОАВ = ∠ОВС = 55°.
ОК – перпендикуляр до сторони ВС, ОК ﬩ ВС.
О – центр вписаного кола у трикутник з радіусом ОК.
Завдання 665
Накресліть кут градусної міри 70°. За допомогою циркуля, косинця і транспортира впишіть у нього коло довільного радіуса.
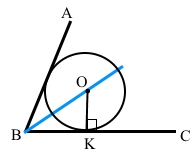
∠АВС = 70°.
ВО – бісектриса кута АВС, ∠ОАВ = ∠ОВС = 35°.
ОК – перпендикуляр до сторони ВС, ОК ﬩ ВС.
О – центр вписаного кола у трикутник з радіусом ОК.
Завдання 666
У трикутнику центр вписаного кола лежить на медіані. Доведіть, що це рівнобедрений трикутник.
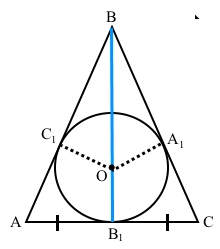
За умовою точка О – центр вписаного кола у трикутник АВС, за означенням вписаного кола С1, А1, В1 – точки дотику. Тоді для дотичних до кола, проведених із точки В, за властивістю відрізків дотичних ВС1 = ВА1.
За умовою ВВ1 – медіана кута В, тобто АВ1 = СВ1. Через вершину В і центр О можна провести тільки одну пряму, тому медіана є бісектрисою.
Для дотичних до кола, проведених із точки А, за властивістю відрізків дотичних АС1 = АВ1, а для дотичних до кола, проведених із точки С, за властивістю відрізків дотичних СА1 = СВ1. Якщо рівні праві частини, тоді ліві АС1 = СА1.
За властивістю вимірювання відрізків АВ = АС1 + ВС1, ВС = СА1 + ВА1, де рівні праві частини рівності, тому АВ = ВС. Отже, за означенням трикутник АВС рівнобедрений.
Завдання 667
У трикутнику центр вписаного кола лежить на висоті. Доведіть, що цей трикутник є рівнобедреним.
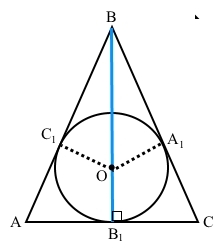
За умовою точка О – центр вписаного кола у трикутник АВС, С1, А1, В1 – точки дотику.
ВВ1 – висота трикутника, тоді ∠ВВ1А = ∠ВВ1С = 90°. Через вершину В і центр О можна провести тільки одну пряму, тому висота є бісектрисою, звідси ∠АВВ1 = ∠В : 2, ∠СВВ1 = ∠В : 2.
Розглянемо прямокутні трикутники АВВ1 і СВВ1. ∠А = 90° – ∠АВВ1 = 90° – ∠В : 2, ∠В = 90° – ∠СВВ1 = 90° – ∠В : 2, звідси ∠А = ∠В. Отже, трикутник АВС – рівнобедрений (за ознакою рівних кутів рівнобедреного трикутника).
Завдання 668
У ∆ABC вписано коло, яке дотикається до сторін AB, AC і BC у точках P, F і M відповідно. Знайдіть AP, PB, BM, MC, CF і FA, якщо AB = 8 см, BC = 6 см, AC = 12 см.
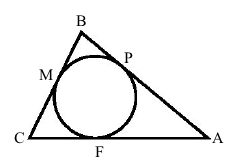
За умовою BC і AB – дотичні з точки B, ВС і АС – дотичні з точки С, АВ і АС – дотичні з точки А.
За властивістю відрізків дотичних, проведених із однієї точки, маємо три пари рівних відрізків: PB = BM, CM = CF, АР = АF.
AP + PB + BM + MC + CF + FA = PABC
2АР + 2ВМ + 2СМ = PABC
АР + ВМ + СМ = PABC /2
PABC /2 = (АВ + ВС + АС)/2 = (8 + 6 + 12) : 2 = 13 (см)
АР = AF = PABC /2 – (ВМ + СМ) = PABC /2 – ВС = 13 – 6 = 7 (см)
ВМ = РВ = PABC /2 – (АР + СМ) = PABC /2 – (АF + FМ) = PABC /2 – AC = 13 – 12 = 1 (см)
CM = CF = PABC /2 – (АР + BМ) = PABC /2 – (АP + PB) = PABC /2 – AB = 13 – 8 = 5 (см)
Відповідь: AP = AF = 7 см, BP = BM = 1 см, СМ = CF = 5 см.
Завдання 669
Знайдіть довжини сторін трикутника, якщо точки дотику кола, вписаного в цей трикутник, ділять його сторони на відрізки, три з яких дорівнюють 4 см, 6 см і 8 см.

За умовою BC і AB – дотичні з точки B, ВС і АС – дотичні з точки С, АВ і АС – дотичні з точки А.
За властивістю відрізків дотичних, проведених із однієї точки, маємо три пари рівних відрізків: PB = BM = 4 см, CM = CF = 6 см, АР = АF = 8 см.
ВС = ВМ + СМ = 4 см + 6 см = 10 см
АС = AF + CF = 8 см + 6 см = 14 см
АВ = РВ + АР = 4 см + 8 см = 12 см
Відповідь: 10 см, 12 см, 14 см.
Завдання 670
Коло, вписане в рівнобедрений трикутник, ділить його бічну сторону на відрізки 3 см і 4 см, починаючи від основи. Знайдіть периметр трикутника.

За умовою трикутник АВС – рівнобедрений з основою АС, BC і AB – дотичні з точки B, ВС і АС – дотичні з точки С, АВ і АС – дотичні з точки А.
За властивістю відрізків дотичних, проведених із однієї точки, маємо три пари рівних відрізків: СВ1 = СA1 = 3 см, ВА1 = BС1 = 4 см, АС1 = АВ1.
Оскільки трикутник рівнобедрений, тоді бісектриса ВВ1 є медіаною, тому АВ1 = СВ1 = 3 см = АС1.
РАВС = АВ + ВС + АС = (АС1 + ВС1) + (ВА1 + СА1) + (АВ1 + СВ1) = 4СВ1 + 2ВА1 = 4 • 3 см + 2 • 4 см = 20 см.
Відповідь: 20 см.
Завдання 671
Коло, вписане в рівнобедрений трикутник, ділить його бічну сторону на відрізки 5 см і 7 см, починаючи від вершини, що протилежна основі. Знайдіть периметр трикутника.
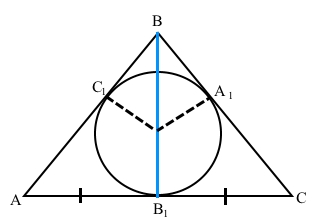
За умовою трикутник АВС – рівнобедрений з основою АС, BC і AB – дотичні з точки B, ВС і АС – дотичні з точки С, АВ і АС – дотичні з точки А.
За властивістю відрізків дотичних, проведених із однієї точки, маємо три пари рівних відрізків: СВ1 = СA1, ВC1 = BA1 = 5 см, АС1 = АВ1 = 7 см.
Оскільки трикутник рівнобедрений, тоді бісектриса ВВ1 є медіаною, тому AB1 = CB1, звідси AC1 = АВ1 = СВ1 = CA1 = 7 см
РАВС = АВ + ВС + АС = (АС1 + ВС1) + (ВА1 + СА1) + (АВ1 + СВ1) = 4AC1 + 2BC1 = 4 • 7 см + 2 • 5 см = 38 см.
Відповідь: 38 см.
Вправи для повторення
Завдання 672
Доведіть, що висоти, проведені до бічних сторін гострокутного рівнобедреного трикутника, між собою рівні.
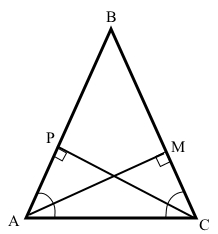
За умовою трикутник АВС – рівнобедрений з основою АС, тоді ∠А = ∠С.
АМ – висота до бічної сторони ВС (АМ ﬩ ВС), СР – висота до бічної сторони АВ (СР ﬩ АВ).
АС – спільна сторона прямокутних трикутників РСА і МАС, ∠А = ∠С, тому ∆РСА = ∆МАС (за гіпотенузою і гострим кутом). Отже, відповідні сторони, що є висотами, АМ = СР.
Завдання 673
Гострі кути прямокутного трикутника відносяться як 2 : 3. Знайдіть кут між бісектрисою і висотою, проведеними з вершини прямого кута.
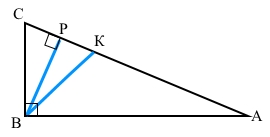
Нехай АВС – прямокутний трикутник, де ∠В = 90°.
Відрізок ВК – бісектриса кута В, тому ∠СВК = ∠В : 2 = 90° : 2 = 45°.
У трикутнику АВС проти більшої сторони ВА лежить більший кут ∠С, тому ∠С : ∠А = 3 : 2
Сума гострих кутів прямокутного трикутника АВС дорівнює 90°.
Нехай 2х (°) – гострий кут А, 3х (°) – гострий кут С. Складемо рівняння.
2х + 3х = 90
5х = 90
х = 90 : 5
х = (50 + 40) : 5
х = 18 (°) – градусна міра частини.
3х = 18 • 3 = (10 + 8) • 3 = 30 + 24 = 54 (°) – гострий кут С.
Для трикутника СКВ знайдемо ∠СКВ = 180° – (54° + 45°) = 81°. Точка Р належить відрізку СК, тому ∠СКВ = ∠РКВ = 81°.
Для прямокутного трикутника ВРК знайдемо РВК = 90° – РКВ = 90° – 81° = 9°, він є шуканим кутом між бісектрисою і висотою, проведеними з вершини прямого кута.
Відповідь: 9°.
Завдання 674 Яка швидкість поїзда (у км/год), якщо діаметр його колеса дорівнює 120 см і воно робить 360 обертів за хвилину? (Прийміть π = 3)
Розв’язання
1) l = 2πr = πd = 3 • 120 = 360 (cм) = 3,6 (м) – відстань за один оберт (довжина обода колеса).
2) 3,6 • 360 = 1296 (м) – відстань за 1 хв.
3) 1296 • 60 = 77760 (м/год) = 77,76 (км/год)
Відповідь: швидкість потяга 77,76 км/год.
Завдання 675 Квадрат розрізали на вісім квадратів. Чи обов'язково п'ять з них рівні між собою?
Не обов’язково.