Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 24 Коло, описане навколо трикутника, серединний перпендикуляр та його властивість
Завдання 676
Пряма a є серединним перпендикуляром до відрізка MN на малюнку 24.5.
Завдання 677
Коло, описане навколо трикутника, зображено на малюнку 24.9.
Завдання 678
1) Накресліть відрізок MN, довжина якого 5,4 см. За допомогою лінійки з поділками і косинця проведіть серединний перпендикуляр до відрізка MN.
2) Позначте деяку точку P, що належить серединному перпендикуляру, і переконайтеся, що PM = PN.
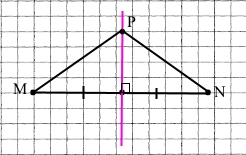
РМ = PN = 3 см 4 мм
Завдання 679
1) Накресліть відрізок AB завдовжки 4,6 см. За допомогою лінійки з поділками і косинця проведіть серединний перпендикуляр до відрізка AB.
2) Позначте деяку точку C, що належить серединному перпендикуляру, і переконайтеся, що CA = CB.
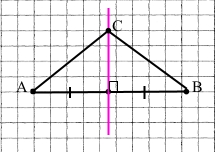
СА = СВ = 3 см 1 мм
Завдання 680 Малюнок 24.10
Точка O – центр кола, описаного навколо різностороннього трикутника ABC. Знайдіть усі пари рівних між собою трикутників на цьому малюнку.
ОМ – серединний перпендикуляр до сторони АВ (АМ = МВ, ОМ ﬩ АВ. Прямокутні трикутники ∆АОМ = ∆ВОМ (за двома катетами).
ОК – серединний перпендикуляр до сторони АС (АК = КС, ОК ﬩ АС. Прямокутні трикутники ∆АОК = ∆СОК (за двома катетами).
ОL – серединний перпендикуляр до сторони CB (CL = LB, ОL ﬩ CB. Прямокутні трикутники ∆CОL = ∆BОL (за двома катетами).
Відповідь: маємо три пари рівних трикутників.
Завдання 681
Скільки кiл можна провести через:
1) Через одну точку можна провести безліч кіл різних радіусів (спільна точка дотику).
2) Через дві точки можна провести безліч кіл різних радіусів (спільна хорда через дві точки).
3) Через три точки, що не лежать на одній прямій, можна провести одне коло (коло, описане навколо трикутника).
Завдання 682
1) Накресліть гострокутний трикутник. За допомогою креслярських інструментів опишіть навколо нього коло.
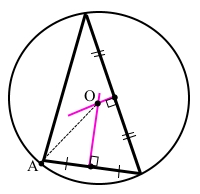
Накреслили гострокутний трикутник.
Знайшли точку перетину серединних перпендикулярів двох сторін трикутника – центр кола.
Описали навколо трикутника коло з центром в точці О і радіусом ОА.
2) Центр кола, описаного навколо гострокутного трикутника, лежить усередині трикутника.
Завдання 683
Накресліть трикутник, два кути якого дорівнюють 60° і 70°. За допомогою креслярських інструментів опишіть навколо нього коло.
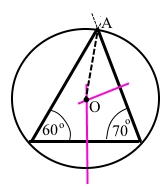
Згідно суми кутів трикутника 180° – (60° + 70°) = 50°. Маємо гострокутний трикутник.
Накреслили гострокутний трикутник із кутами 60° і 70°.
Знайшли точку перетину серединних перпендикулярів двох сторін трикутника – центр кола.
Описали навколо трикутника коло з центром в точці О і радіусом ОА.
Завдання 684
1) Накресліть тупокутний трикутник. За допомогою креслярських інструментів опишіть навколо нього коло.
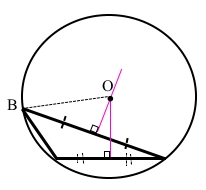
Накреслили тупокутний трикутник.
Знайшли точку перетину серединних перпендикулярів двох сторін трикутника – центр кола.
Описали навколо трикутника коло з центром в точці О і радіусом ОВ.
2) Центр кола, описаного навколо тупокутного трикутника, лежить поза трикутником.
Завдання 685
Накресліть рівнобедрений трикутник з кутом 120° при вершині. За допомогою креслярських інструментів опишіть навколо нього коло.
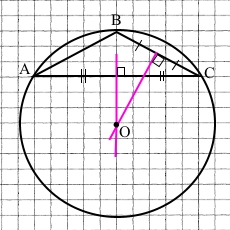
АВС – рівнобедрений трикутник з кутом ∠В = 120°.
Коло з центром у точці О описане навколо трикутника АВС.
Завдання 686
У трикутнику центр описаного кола лежить на медіані. Доведіть, що трикутник рівнобедрений.
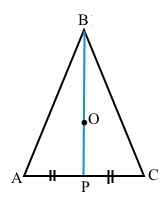
Нехай точка О – центр кола, описаного навколо трикутника АВС, лежить на медіані ВР, проведеній до сторони АС, звідси АP = PС. Оскільки центр описаного кола – це точка перетину серединних перпендикулярів до кожної зі сторін трикутника, то ОР – серединний перпендикуляр до сторони АС, за основною властивістю прямої (через дві точки можна провести тільки одну пряму) ВР – медіана і серединний перпендикуляр до відрізка АС. Тоді за властивістю серединного перпендикуляра до відрізка ВА = ВС. Отже, ∆АВС – рівнобедрений (за означенням).
Завдання 687
У трикутнику центр описаного кола лежить на висоті. Доведіть, що трикутник рівнобедрений.
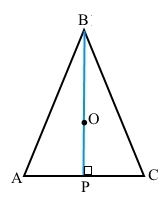
Нехай точка О – центр кола, описаного навколо трикутника АВС, лежить на висоті ВР, проведеній до сторони АС, звідси ВР ﬩ АС. Оскільки центр описаного кола – це точка перетину серединних перпендикулярів до кожної зі сторін трикутника, то ВР – серединний перпендикуляр до сторони АС, за основною властивістю прямої (через дві точки можна провести тільки одну пряму) ВР – висота і серединний перпендикуляр до відрізка АС. Тоді за властивістю серединного перпендикуляра до відрізка ВА = ВС. Отже, ∆АВС – рівнобедрений (за означенням).
Завдання 688
Доведіть, що радіус кола, описаного навколо рівностороннього трикутника, удвічі більший за радіус кола, вписаного в трикутник.
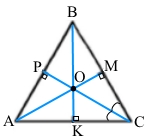
За умовою трикутник АВС – рівносторонній (∠А = ∠В = ∠С = 60°), кожна його бісектриса є медіаною і висотою. Центр вписаного кола – точка перетину бісектрис та центр описаного кола – точка перетину серединних перпендикулярів співпадають у точці О, тому ОM = OP = OK = r – радіуси вписаного кола, а ОА = ОС = ОВ = R – радіуси описаного кола.
СР – бісектриса кута С, тому ∠МСО = 60° : 2 = 30°. У прямокутному трикутнику МОС катет ОМ = 1/2 ОС (катет проти кута 30° дорівнює половині гіпотенузи), звідси ОС = 2ОМ. Отже, R = 2r.
Вправи для повторення
Завдання 689
LM – діаметр кола, хорди KL і KM - рівні між собою. Знайдіть кути трикутника KLM.
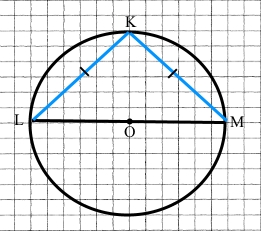
За умовою KL = KM, тоді трикутник LKM – рівнобедрений з основою LM за означенням (дві сторони рівні). За властивістю рівнобедреного трикутника ∠L = ∠M (кути при основі рівні). Трикутник LKM – прямокутний з кутом ∠К = 90° за теоремою про кут, під яким видно діаметр кола (діаметр кола з будь-якої точки видно під прямим кутом). Згідно теореми про суму кутів прямокутного трикутника ∠L + ∠M = 90°,
2∠L = 2∠M = 90°, ∠L = ∠M = 90°/2 = 45°.
Відповідь: ∠К = 90°, ∠L = ∠M = 45°.
Завдання 690
I – точка перетину бісектрис AM і BN рівнобедреного трикутника ABC з основою AB. Доведіть, що IN = IM.
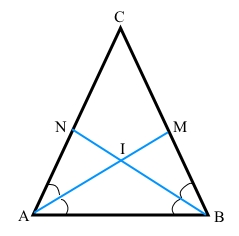
За умовою АМ – бісектриса трикутника з кута А, точка М є СВ; BN – бісектриса трикутника з кута В, N є AC, оскільки точка І – точка перетину бісектрис, І є АМ, І є BN, тому ∠САМ = ∠BAM = ∠NAI = ∠BAI = ∠A/2 і ∠ABN = ∠CBN = ∠ABI = ∠MBI = ∠B/2.
За умовою ∆АВС – рівнобедрений з основою АВ, звідси за властивістю рівнобедреного трикутника ∠А = ∠В, тому ∠САМ = ∠BAM = ∠ABN = ∠CBN (∠NAI = ∠BAI = ∠ABI = ∠MBI)
Відрізок АС – спільна сторона трикутників ABN і BAM, ∠А = ∠B, ∠ВАМ = ∠ABN, тому ∆АBN = ∆ВАМ (за першою ознакою – стороною і прилеглими кутами), звідси рівні відповідні сторони AN = BM і кути ∠ANB = ∠BMA (∠ANI = ∠BMI).
Трикутники ∆AIN = ∆BIN (за першою ознакою). Отже відповідні сторони IN = IM.
Життєва математика
Завдання 691
Площа земельної ділянки, що має форму прямокутника, дорівнює 9 га, ширина ділянки дорівнює 150 м. Знайдіть довжину огорожі навколо цієї ділянки.
Короткий запис
Ширина — 150 м
Довжина — ? м
S — 9 га
Р — ? м
Розв’язання
9 га = 9 • 10 000 м2 = 90 000 м2
1) 90 000 : 150 = 9000 : 15 = 9000 : 3 : 5 = 3000 : 5 = 600 (м) – довжина ділянки.
2) Р = (600 + 150) • 2 = 1200 + 300 = 1500 (м)
Відповідь: довжина огорожі 1500 метрів.
Підготуйтеся до вивчення нового матеріалу
Завдання 692
Накресліть коло, радіус якого 3 см. Проведіть у цьому колі діаметр і хорду.
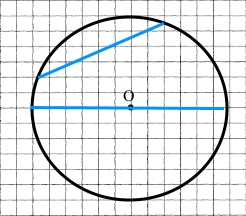
Хорда – відрізок, що сполучає дві точки кола.
Діаметр – хорда, яка проходить через центр кола.
Завдання 693 Малюнок 24.11
1) Точка O – центр кола. Знайдіть ∠COB, якщо ∠CAO = 50°.
Відрізки ОА = ОС – радіуси кола з центром в точці О, тому ∆АОС – рівнобедрений з основою АС (за означенням), за властивістю рівнобедреного трикутника ∠САО = ∠АСО = 50° (кути при основі рівні). Кут СОВ – зовнішній кут трикутника АОС, за властивістю зовнішнього кута ∠СОВ = ∠САО + ∠АСО = 50° + 50° = 100° (зовнішній кут дорівнює сумі двох кутів не суміжних з ним).
Відповідь: ∠СОВ = 100°.
2) Точка O – центр кола. Знайдіть ∠CAO, якщо ∠COB = 110°.
Відрізки ОА = ОС – радіуси кола з центром в точці О, тому ∆АОС – рівнобедрений з основою АС (за означенням), за властивістю рівнобедреного трикутника ∠САО = ∠АСО (кути при основі рівні). Кут СОВ – зовнішній кут трикутника АОС, за властивістю зовнішнього кута (зовнішній кут дорівнює сумі двох кутів не суміжних з ним) ∠СОВ = ∠САО + ∠АСО = 2∠САО, звідси ∠САО = ∠СОВ/2 = 110° : 2 = 55°.
Відповідь: ∠САО = 55°.
Завдання 694 Малюнок 24.13
1) Точка O – центр кола, а точка M – точка дотику прямої a з колом. Знайдіть ∠NMB, якщо ∠MON = 140°.
За умовою М – точка дотику до кола з центром у точці О, тому ОМ ﬩ а, ∠ОМВ = 90°.
Відрізки ОМ = ON – радіуси кола, ∆MON – рівнобедрений з основою MN (за означенням), ∠OMN = ∠ONM за властивістю рівнобедреного трикутника (кути при основі рівні).
Із теореми про суму кутів трикутника випливає ∠OMN + ∠ONM = 2∠OМN = 180° – ∠MON, звідки ∠OМN = (180° – ∠MON) : 2 = (180° – 140°) : 2 = 20°.
За властивістю вимірювання кутів ∠ОМВ = ∠OMN + ∠NMB, тому ∠NMB = ∠OMB – ∠OMN = 90° – 20° = 70°.
Відповідь: ∠NMB = 70°.
2) Точка O – центр кола, а точка M – точка дотику прямої a з колом. Знайдіть ∠MON, якщо ∠BMN = 65°.
За умовою М – точка дотику до кола з центром у точці О, тому ОМ ﬩ а, ∠ОМВ = 90°.
За властивістю вимірювання кутів ∠ОМВ = ∠OMN + ∠BMN, тому ∠OMN = ∠OMB – ∠BMN = 90° – 65° = 25°.
Відрізки ОМ = ON – радіуси кола, ∆MON – рівнобедрений з основою MN (за означенням), ∠OMN = ∠ONM за властивістю рівнобедреного трикутника (кути при основі рівні).
Із теореми про суму кутів трикутника випливає ∠MON = 180° – (∠OMN + ∠ONM) = 180° – 2∠OMN = 180° – 2 • 25° = 130°.
Відповідь: ∠MON = 130°.
Цікаві задачі
Завдання 695
Відрізок 32 см завдовжки поділено двома точками на три не рівних між собою відрізки. Відстань між серединами крайніх відрізків дорівнює 20 см. Знайдіть довжину середнього відрізка.
А—С—M————L——D——В
Нехай точка С – середина відрізка АМ, АС = СМ, а точка D – середина відрізка LB, LD = DB.
За властивістю вимірювання відрізків АВ = АС + CD + DB, звідки АС + DB = AB – CD = 32 – 20 = 12 (см)
Також АВ = АС + СМ + ML + LD + DB = ML + 2АС + 2DB, AB = ML + 2(AC + DB), тоді
ML = AB – 2(AC + DB) = 32 – 2 • 12 = 32 – 24 = 8 (см)
Відповідь: 8 см.